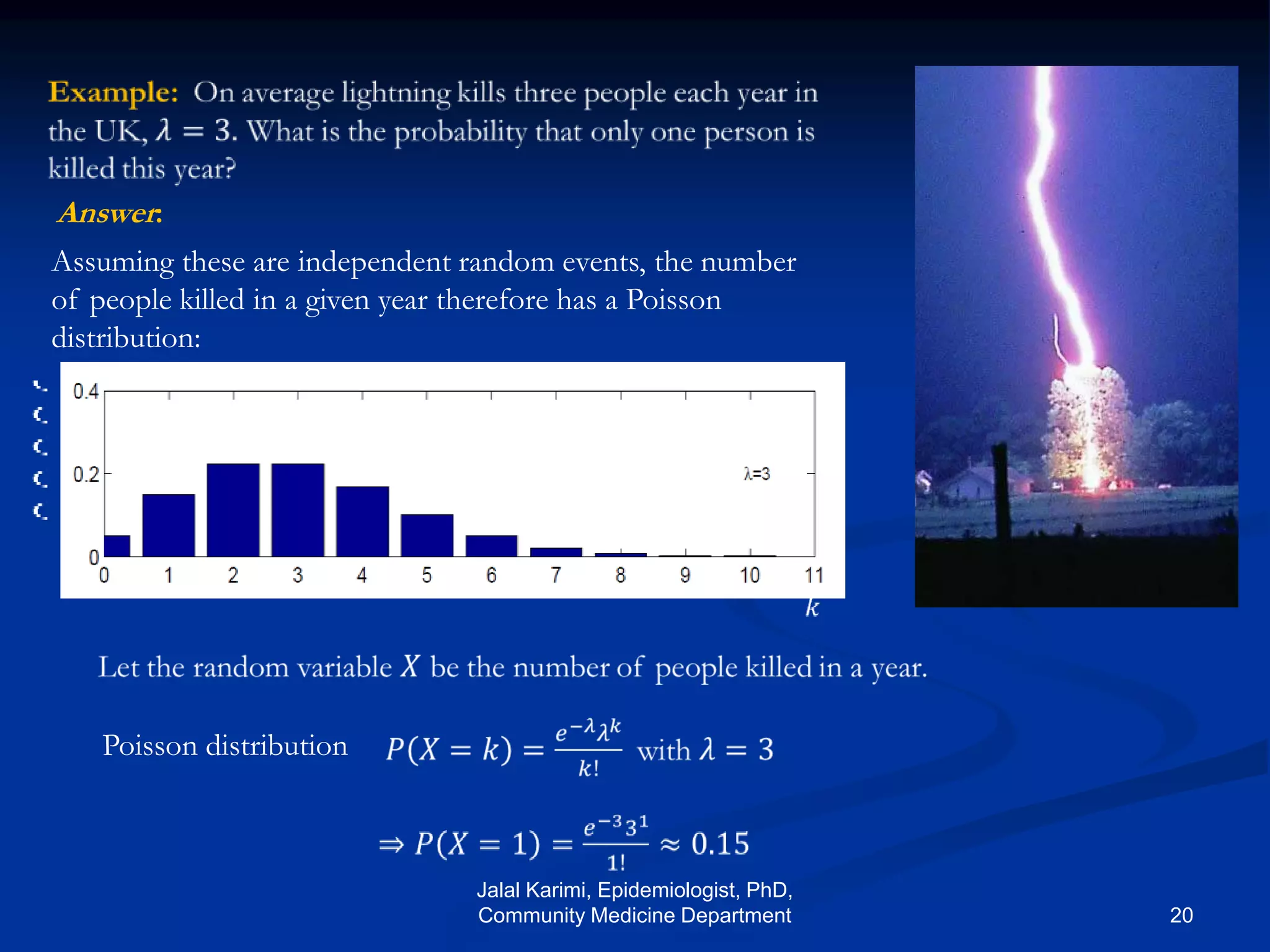
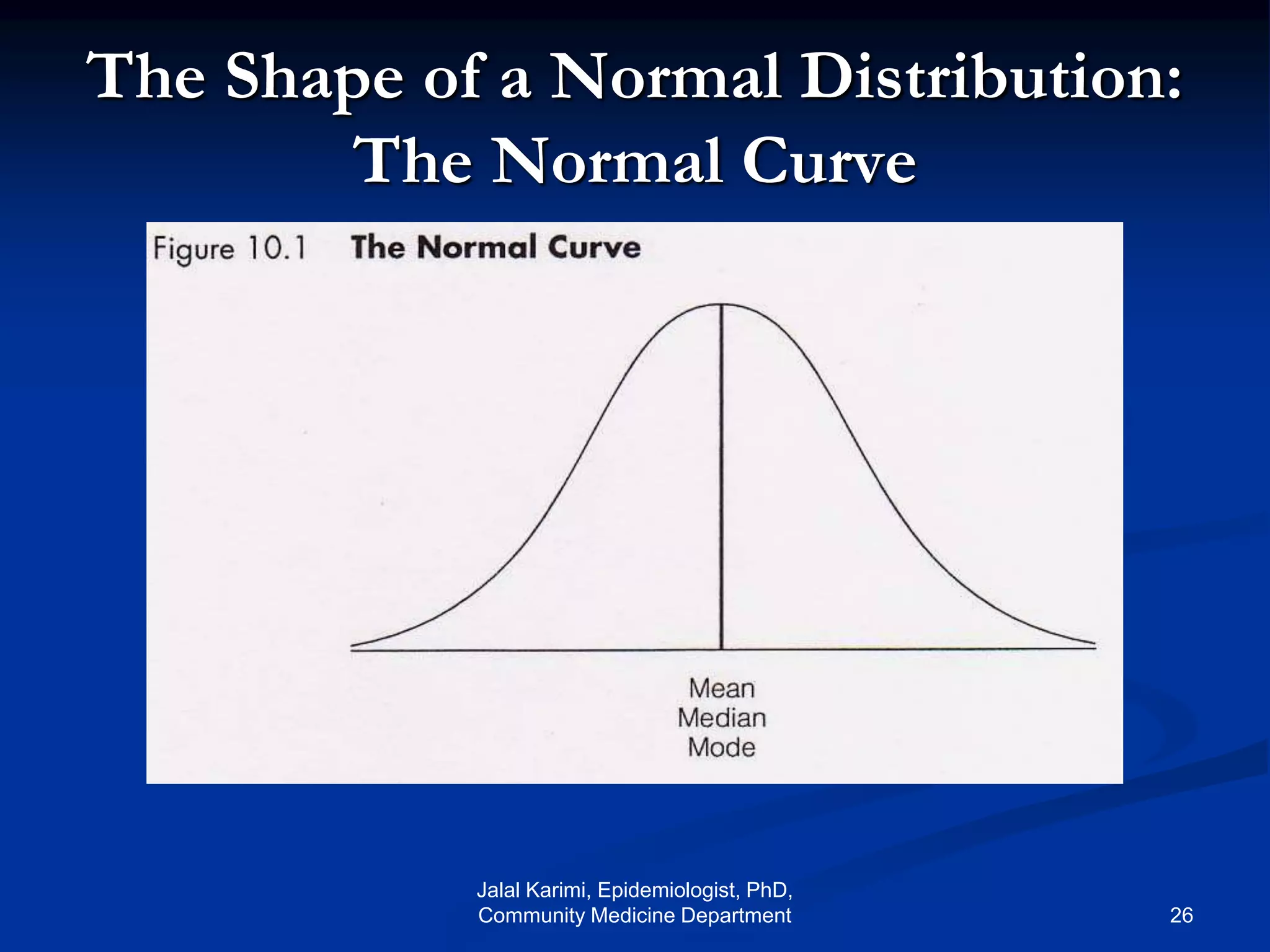
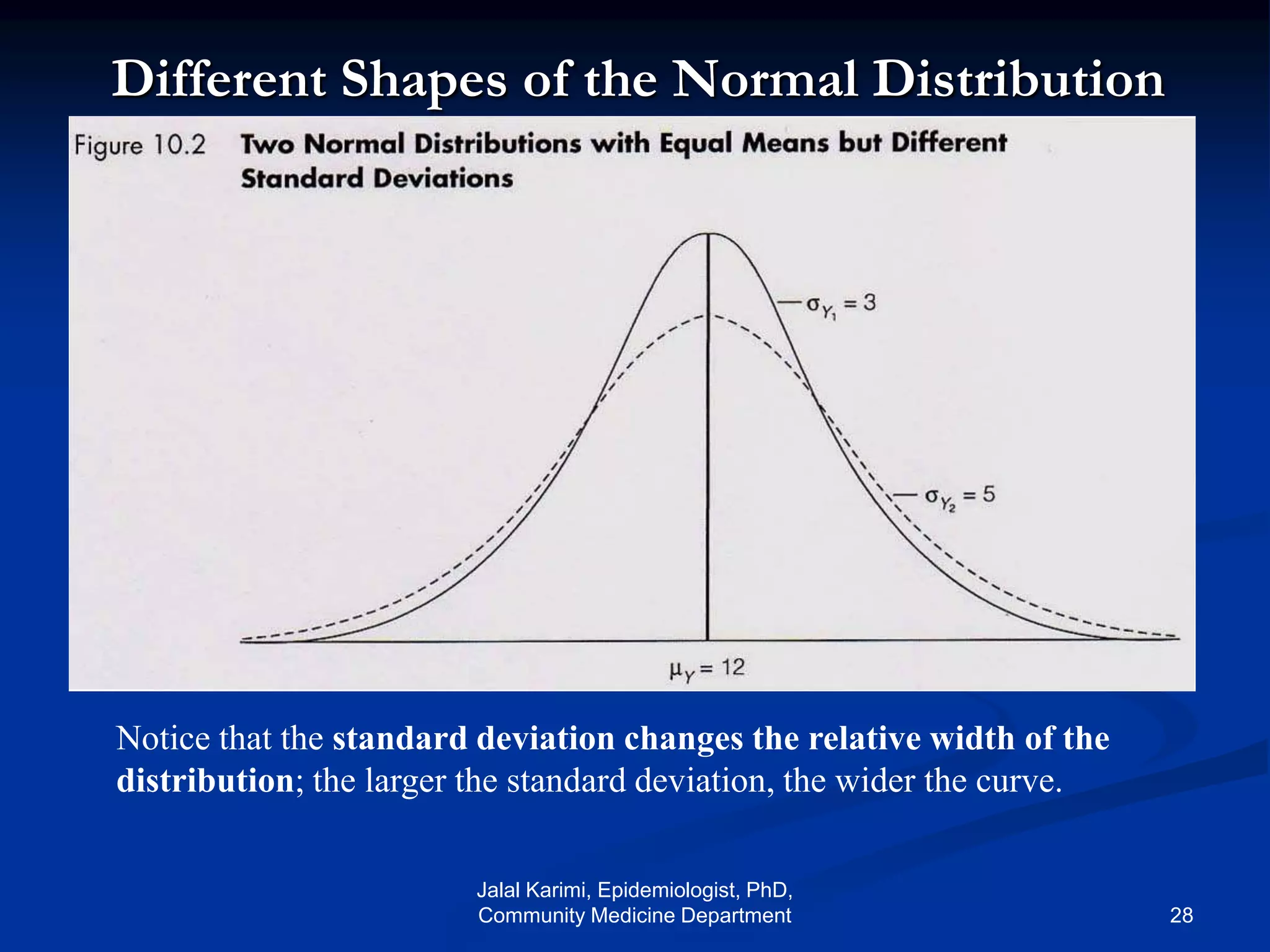
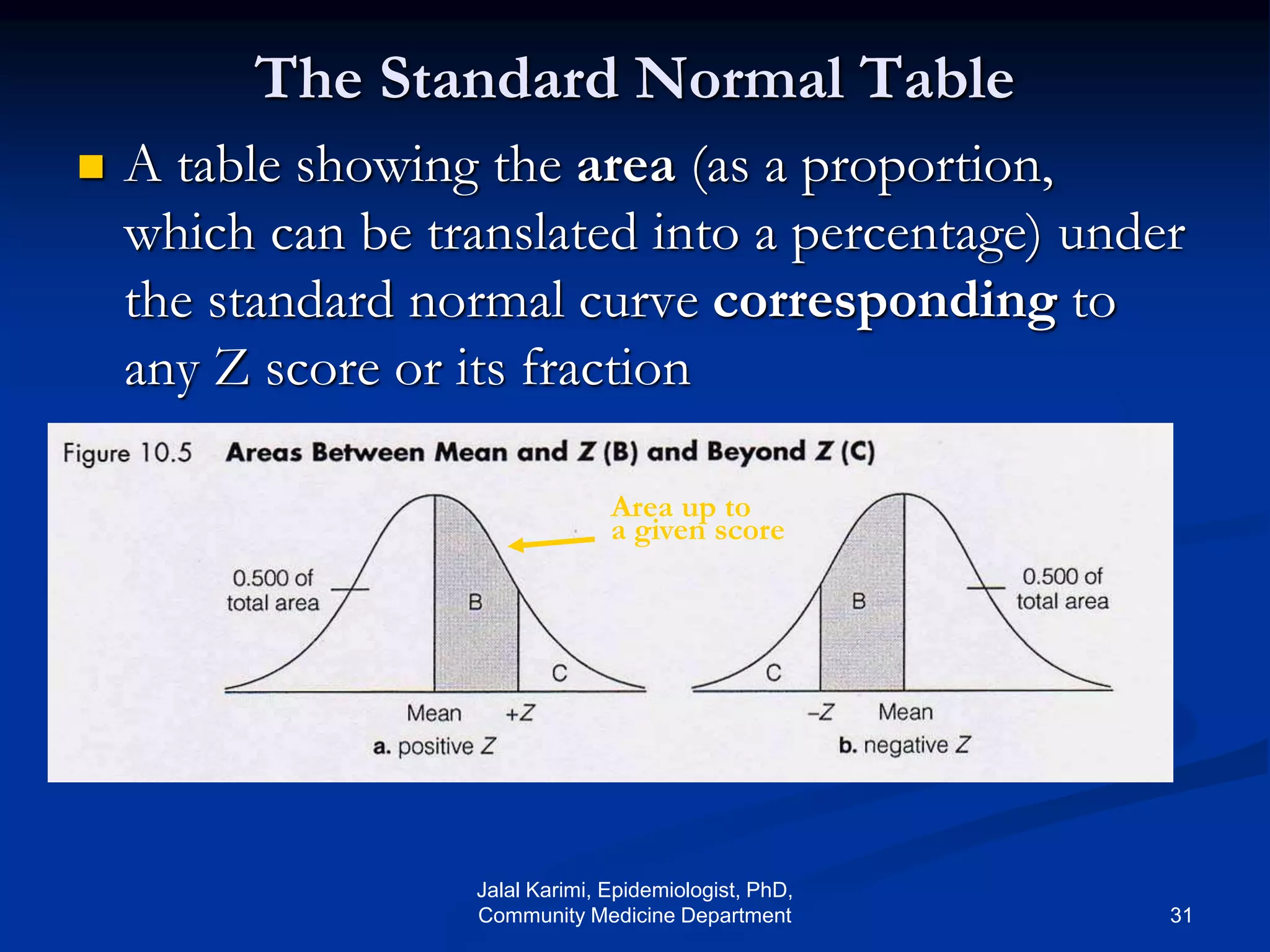
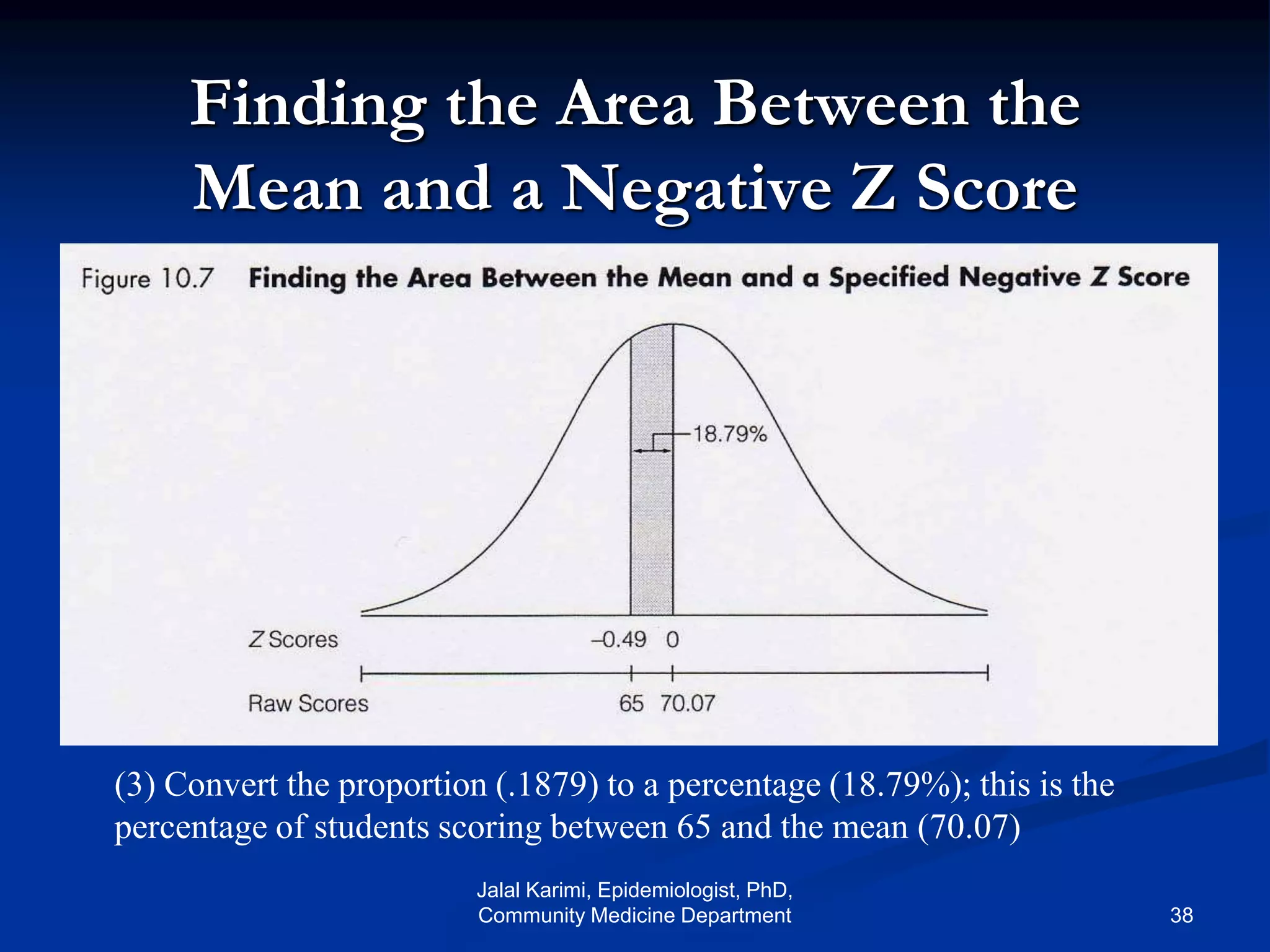
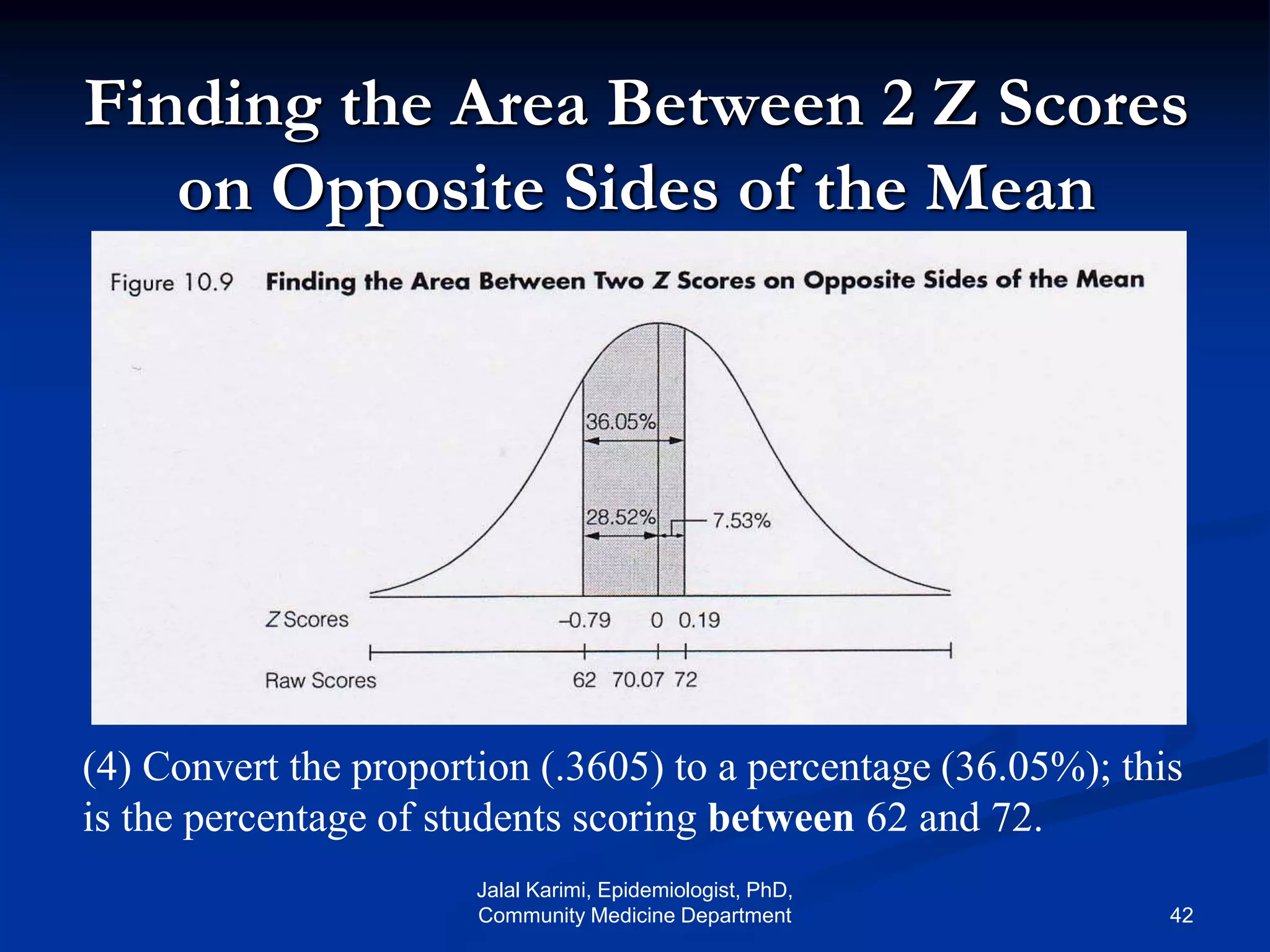
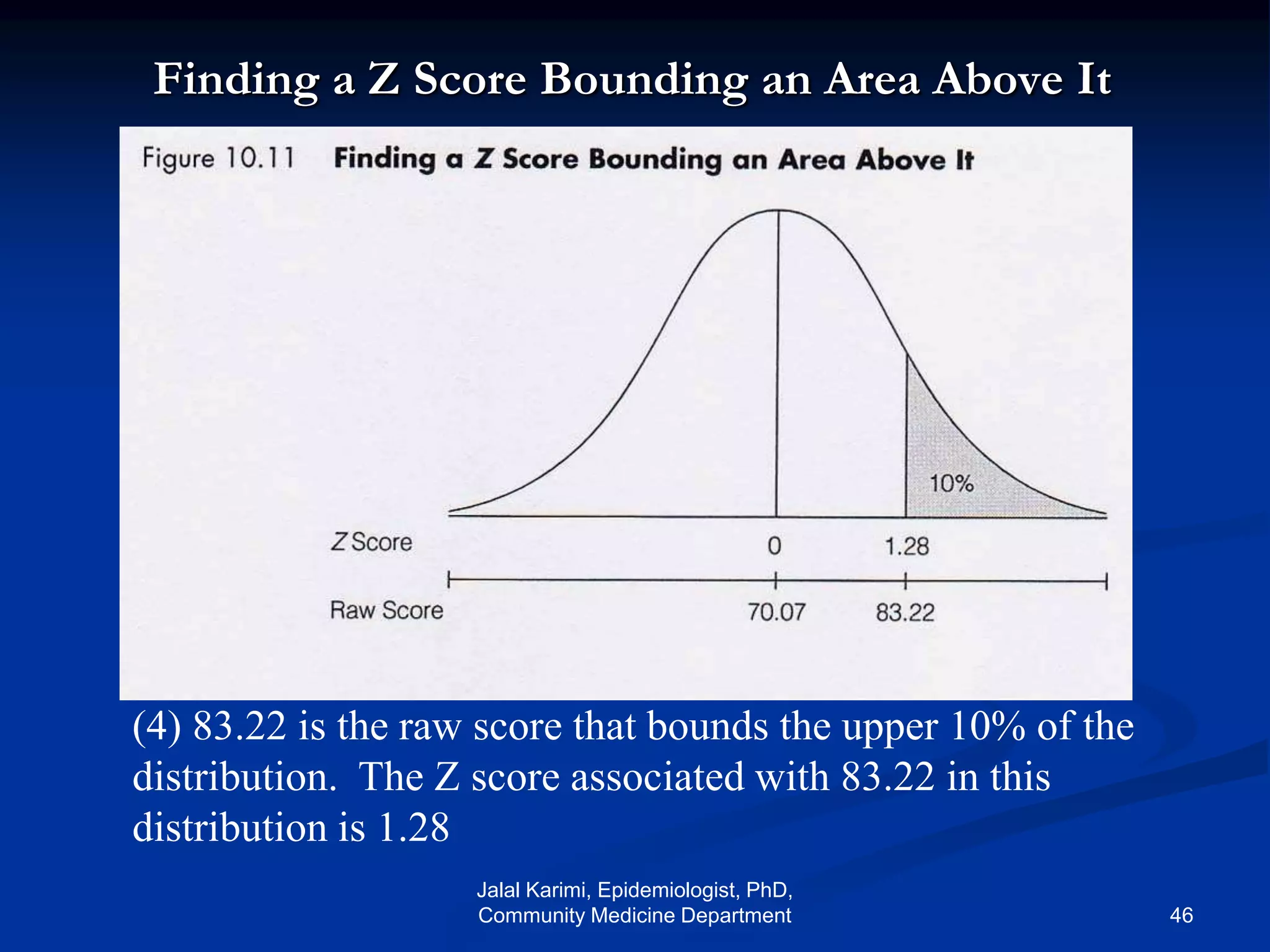
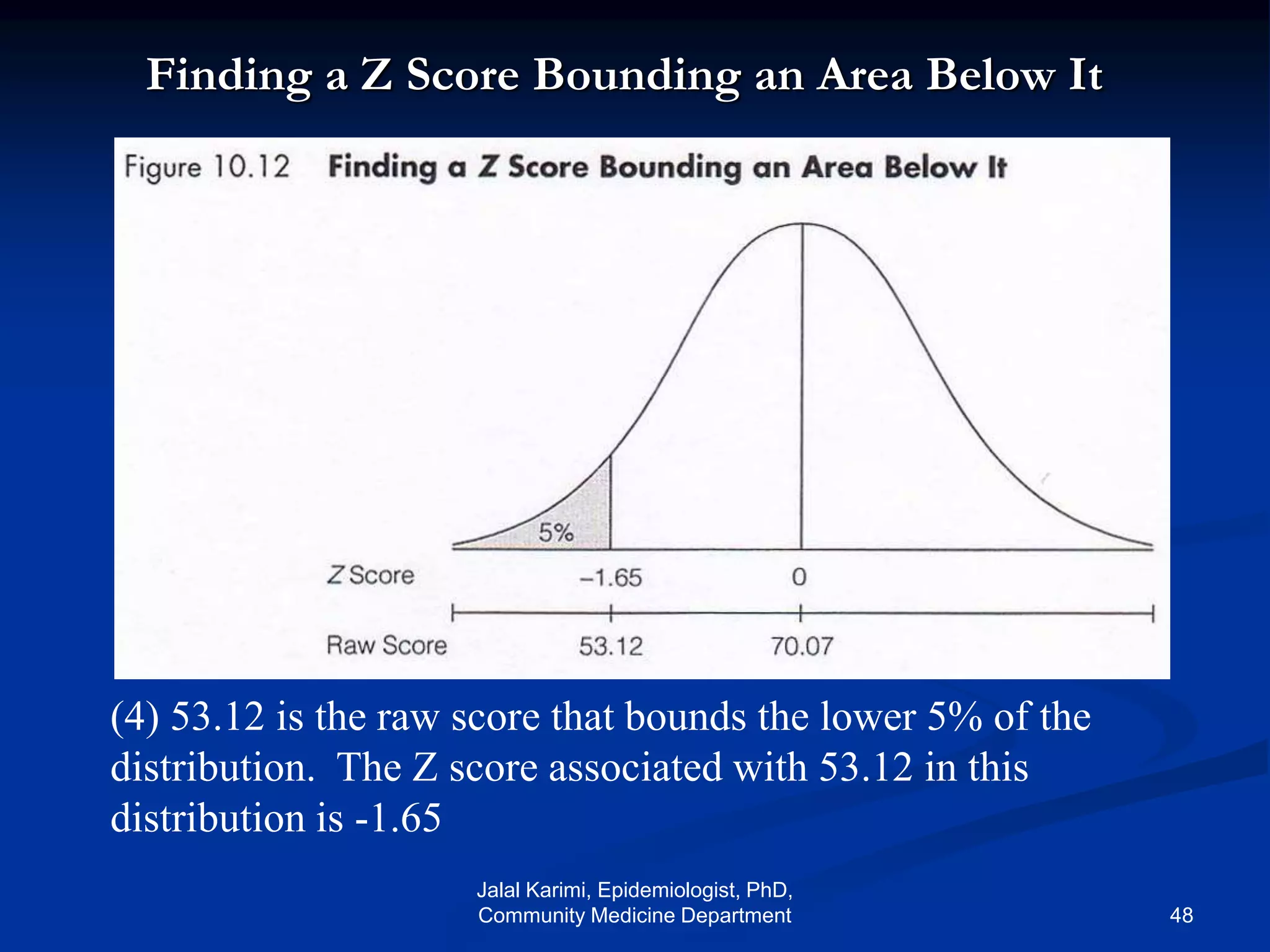
This document provides an introduction to probability distributions and biostatistics. It discusses three fundamental probability distributions used in statistics: the binomial distribution, Poisson distribution, and normal distribution. For the binomial distribution, it provides examples of how to calculate probabilities using the binomial probability formula. It also gives an example showing how the binomial distribution can be used to analyze results from a clinical trial on a new kidney cancer therapy.