PPS Sampling Technique Chapter
•Download as PPTX, PDF•
7 likes•5,993 views
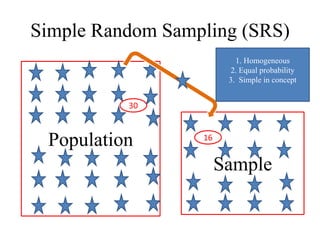
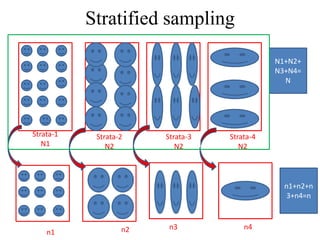
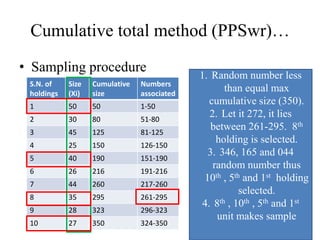
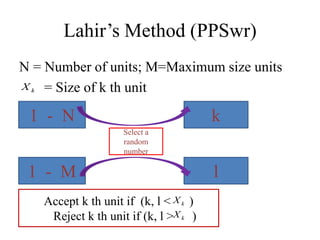
1) The document discusses probability proportional to size (PPS) sampling techniques, including PPS sampling with and without replacement. 2) Cumulative total and Lahiri's methods are described for PPS sampling with replacement, while general selection procedure, Sen-Midzuno method, and Narain's scheme are covered for PPS sampling without replacement. 3) Estimators for population totals, means, variances, and inclusion probabilities are defined for PPS samples. Both ordered and unordered estimators are discussed.
Recommended
More Related Content
What's hot
What's hot (20)
Similar to PPS Sampling Technique Chapter
Similar to PPS Sampling Technique Chapter (20)
More from Khulna University
More from Khulna University (8)
Recently uploaded
Recently uploaded (20)
PPS Sampling Technique Chapter
- 1. Stat-3203: Sampling Technique-II (Chapter-1: PPS sampling) Md. Menhazul Abedin Lecturer Statistics Discipline Khulna University, Khulna-9208 Email: menhaz70@gmail.com
- 2. Main book
- 3. Outline… Background study of PPS sampling or Why PPS sampling (re45ppview of SRS, Stratified, Systematic etc) What is PPS sampling Sampling unit selection procedure Estimators (ordered & unordered)
- 4. Simple Random Sampling (SRS) Population Sample 30 16 1. Homogeneous 2. Equal probability 3. Simple in concept
- 5. Simple Random Sampling (SRS) Procedure of selecting a random sample Lottery method Use of random number table Remind basic concept of estimating mean, total, variance and their properties. Different schemes of using random number table.
- 7. Stratified sampling • Heterogeneous • Do SRS in each stratum • Calculate mean, total, variance or measuring statistics for each strata and combine them. • Study the allocation rules Equal allocation Proportional allocation Neyman allocation Optimum allocation • Gain in precision
- 9. Systematic Sampling • Sample selection procedure Linear systemic sampling Circular systematic • Estimate total, mean and variance • Study their properties • Gain in precision
- 10. Unequal size sample unit Draw a sample of four garden
- 11. Unequal size sample unit • Architecture= 350 student • CSE = 400 • URP= 700 • ECE= 300 • Mathematics= 250 • Physics= 130 • Chemistry= 80 • Statistics= 50 Select three discipline How??? SRS?? Stratified?? Systematic?? Ans: No
- 12. Probability Proportional to Size(PPS) • How to draw a sample?
- 13. Probability proportional to size(PPS) • Procedures of selecting a sample with replacement Cumulative total method Lahiri’s method • Procedures of selecting a sample without replacement General selection procedure Sen-midzuno method Narain’s scheme of sample selection
- 14. Cumulative total method (PPSwr)… • Sampling procedure S.N. of holdings Size (Xi) Cumulative size Numbers associated 1 50 50 1-50 2 30 80 51-80 3 45 125 81-125 4 25 150 126-150 5 40 190 151-190 6 26 216 191-216 7 44 260 217-260 8 35 295 261-295 9 28 323 296-323 10 27 350 324-350 1. Random number less than equal max cumulative size (350). 2. Let it 272, it lies between 261-295. 8th holding is selected. 3. 346, 165 and 044 random number thus 10th , 5th and 1st holding selected. 4. 8th , 10th , 5th and 1st unit makes sample
- 15. Cumulative total method (PPSwr)… • Drawback : This procedure involves writing down the successive cumulative totals. This is time consuming and tedious if the number of units in the population is large.
- 16. Lahir’s Method (PPSwr) N = Number of units; M=Maximum size units = Size of k th unit 1 - N l1 - M k kX Select a random number Accept k th unit if (k, l < ) Reject k th unit if (k, l > ) kX kX
- 17. Lahir’s Method(1951) • Referring to the random number table, the pair is (10, 13). Hence the 10 th unit is selected in the sample. • Similarly, choosing other pairs, we can have (4, 26), (5, 35), (7,26). (4, 26) rejected. Why??? • Another pair (8, 16) . • Sample is 10, 5, 7 and 8 th unit
- 18. Lahir’s Method(1951) • Advantage: – It does not require writing down all cumulative totals for each unit. – Sizes of all the units need not be known before hand. We need only some number greater than the maximum size and the sizes of those units which are selected by the choice of the first set of random numbers 1 to N for drawing sample under this scheme.
- 19. Lahir’s Method(1951) • Disadvantage: – It results in the wastage of time and efforts if units get rejected. The probability of rejection 1 − 𝑋 𝑀 . • The expected numbers of draws required to draw one unit 𝑀 𝑋 . • This number is large if 𝑀 is much larger than 𝑋
- 20. Journey: Sample to Population • Total, Mean, Variance Sample Sample mean Sample variance Sample total Population Population mean Population variance Population total • Sample total/mean with unbiased/biased estimator pop total/mean having population variance. • Sample variance unbiased/biased estimator of pop variance
- 21. Journey: Sample to Population 𝐸 𝑡 /𝑚 = 𝑇 /𝑀 with variance 𝑉. and 𝐸 𝑣 = 𝑉 𝐸 𝑡 /𝑚 = 𝑇 /𝑀 with variance 𝑣 Estimators Sample Population Total 𝑡 𝑇 Mean 𝑚 𝑀 Variance 𝑣 𝑉
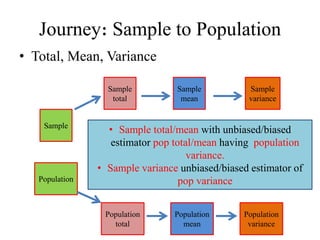
- 22. Expectation Sample-1 Sample-2 Sample-3 Sample-k 𝑠1 𝑠2 𝑠3 𝑠 𝑘 𝐸𝑥𝑝𝑒𝑐𝑡𝑎𝑡𝑖𝑜𝑛 𝐸[𝑠] = 1 𝑘 𝑖=1 𝑘 𝑠𝑖 𝑠𝑖 be any statistic like mean variance, standard deviation … … … … … … 𝑃𝑜𝑝 𝑛 𝑠𝑖𝑧𝑒 = 𝑁 Sample size=n Sample 𝑁 𝑛 = 𝑘
- 23. IID random variables 𝑥1 𝑥2 𝑥 𝑛𝑥3 𝐷𝑖𝑠𝑡 𝑛 𝐷𝑖𝑠𝑡 𝑛 𝐷𝑖𝑠𝑡 𝑛 𝐷𝑖𝑠𝑡 𝑛 Look like twin but not. They comes from different mother. IID random variables … … …
- 24. Defining random variale… • 𝑦𝑖 = Value of the characreristics under study (𝑦𝑖 ?? ambiguity?? Next slide) • 𝑁 = Population size • 𝑝𝑖 = 𝑋𝑖/𝑋 • 𝑧𝑖 = 𝑦 𝑖 𝑝 𝑖 ; 𝑖 = 1, 2, 3, … , 𝑛 IID random variable....... Why ???? • 𝑝𝑖 = 1 𝑁 Simple Random Sampling
- 25. Example 5.3 • Selected sample (cummulative/Lahiri’s method) Area under Crop 5.2 5.9 3.9 4.2 4.7 4.8 4.9 6.8 4.7 5.7 Yield of crop 28 29 30 22 24 25 28 37 26 32 Area under Crop 5.2 5.2 4.9 4.0 1.3 7.4 7.4 4.8 6.2 6.2 Yield of crop 25 38 31 16 6 61 61 29 47 47 Size (X) Value of the characteristic under study (Y) (N=100, n=20)
- 26. Estimators… Theorem 5.3.1: In pps sampling, wr, an unbiased estimator of the population total Y is given by 𝑌𝑝𝑝𝑠 = 1 𝑛 1 𝑛 (𝑦𝑖/𝑝𝑖) With its sampling variance 𝑉( 𝑌𝑝𝑝𝑠) = 1 𝑛 1 𝑁 𝑝𝑖 ( 𝑦 𝑖 𝑝 𝑖 − 𝑌)2 *** find unbiased estimator of mean.... ***See corollary
- 27. Estimators… • Theorem: In pps sampling, wr, an unbiased estimator of 𝑉( 𝑌𝑝𝑝𝑠)is given by • 𝑣( 𝑌𝑝𝑝𝑠) = 1 𝑛(𝑛−1) 1 𝑛 ( 𝑦 𝑖 𝑝 𝑖 − 𝑌𝑝𝑝𝑠)2 = 1 𝑛(𝑛−1) [ 1 𝑛 ( 𝑦 𝑖 𝑝 𝑖 )2 −𝑛 𝑌𝑝𝑝𝑠 2 ]
- 28. Gain due to pps sampling... • Study gain due to PPS sampling with replacement
- 29. Example 5.3 • 𝑦𝑝𝑝𝑠 = 1 𝑛𝑁 1 𝑛 (𝑦𝑖/𝑝𝑖) = 𝑋 𝑛𝑁 1 𝑛 (𝑦𝑖/𝑥𝑖) = 484.5 20 ∗ 100 ∗ 120.5930 = 29.11 • 𝑣( 𝑦𝑝𝑝𝑠) = 1 𝑛 𝑛−1 𝑁2 [ 1 𝑛 𝑦 𝑖 𝑝 𝑖 2 − 𝑛 𝑌𝑝𝑝𝑠 2 ] = 1 20∗19∗100∗100 171249828.1 − 20 ∗ 155785427.3 = 4.06957916 ≅ 4 • Stadard error= 𝑣( 𝑦𝑝𝑝𝑠 = 4 = 2
- 31. PPS Sampling WoR • It is difficult to draw a PPS sample without replacement. Over 50 methods have been proposed but none is perfect.
- 32. Techniques… • General selection procedure • Sen-Midzuno sample selection • Narain’s scheme of sampe selection • Systematic PPS method (Madow (1949) • Durbin (1967) method Our interest
- 33. PPS sampling WoR • General selection procedure 𝑝𝑖 = 𝑋𝑖/𝑋 Select a pair of random numbers 𝑖, 𝑗 𝑠. 𝑡. ( 𝑖 ≤ Orchard 1 2 3 4 5 6 7 8 Trees 50 30 25 40 26 44 20 35 Orchard 1 2 3 4 Blank 5 6 7 Trees 50 30 25 40 44 20 35
- 34. PPS sampling without replaceent… • The first order incluson probability for unit 𝑖 is the probability that 𝑖 is included in a sample of size n and is given by 𝜋𝑖 = 𝑠∋𝑖 𝑝(𝑠) . • The second order inclusion probability for unit 𝑖 and 𝑗 is defined as the probability that the two units 𝑖 and 𝑗 are included in a sample of size n 𝜋𝑖𝑗 = 𝑠∋𝑖,𝑗 𝑝(𝑠) .
- 35. Example • A={1,2,3} • 𝑠1 ={1,2}, 𝑠2 ={1,3}, 𝑠3 ={2,3} • 𝑝(𝑠1) = 1 3 𝑝(𝑠2) = 1 3 𝑝(𝑠3) = 1 3 • 𝜋1 = 1 3 + 1 3 = 2 3 𝜋2 = 1 3 + 1 3 = 2 3 • 𝜋3 = 1 3 + 1 3 = 2 3 • 𝜋1 + 𝜋2 + 𝜋3 = 2 3 + 2 3 + 2 3 = 2
- 36. Property: Inclusion probability • 𝑖=1 𝑁 𝜋𝑖 = 𝑛 • 𝑗=1 𝑁 𝜋𝑖𝑗 = (𝑛 − 1) 𝜋𝑖 • 𝑖=1 𝑁 𝑗=1 𝑖≠𝑗 𝑁 𝜋𝑖𝑗 = 𝑛 − 1 𝑛
- 37. Sen-Midzuno… • First unit from N sized population Without replacement • (n-1)unit from remaining (N-1) Simple random sampling 𝜋𝑖 = 𝑝𝑖 + 1 − 𝑝𝑖 𝑛−1 𝑁−1 = 𝑁−𝑛 𝑁−1 𝑝𝑖 + 𝑛−1 𝑁−1 , 1 ≤ 𝑖 ≤ 𝑁 𝜋𝑖𝑗 = 𝑝𝑖 𝑛−1 𝑁−1 + 𝑝𝑗 𝑛−1 𝑁−1 + (1 − 𝑝𝑖 − 𝑝𝑖) 𝑛−1 𝑁−1 𝑛−2 𝑁−2 1 ≤ 𝑖 ≠ 𝑗 ≤ 𝑁
- 38. Sen-Midzuno… • Higher order inclusion probabilities • 𝜋𝑖𝑗…𝑞 = 1 𝑁−1 𝑛−1 (𝑝𝑖 + 𝑝𝑗 + ⋯ + 𝑝 𝑞)
- 39. Ordered and unordered estimator • Ordred estimator: Incorporate sampling unit’s order. Need only conditional probability not inclusion probability. • Unordered estimator: Free from order concept of sampling unit’s ordes. Incorporate inclusion probability.
- 40. Ordered and unordered estimator • Das-Raj’s ordered estimator→ No need inclusion probability • Horvitz-Thompson estimator (H-T estimator) • Murthy’s estimator Unordered estimator need inclusion probability
- 41. Das-Raj ordered estimator(n=2) • 𝑦1 → 𝑝1 and 𝑦2 → 𝑝2 [Initial probabilities] • Define two random variable – 𝑧1 = 𝑦1 𝑝1 – 𝑧2 = 𝑦1 + 𝑦2(1 − 𝑝1)/𝑝2 • Des-Raj’s total – 𝑌𝐷 =(𝑧1 + 𝑧2)/2 = 𝑦1 1+𝑝1 𝑝1 + 𝑦2 1−𝑝1 𝑝2
- 42. Des-Raj ordered estimator(n=2) • Theorem 5.8.1 In PPS sampling, wor, the estimator 𝑌𝐷 isan unbiased estimator andits sampling variance is given by 𝑉 𝑌𝐷 = 1 − 1 2 𝑖 𝑁 𝑝𝑖 2 1 2 𝑖 𝑁 𝑦𝑖 𝑝𝑖 − 𝑌 2 𝑝𝑖 − 1 4 𝑖 𝑁 𝑦𝑖 𝑝𝑖 − 𝑌 2 𝑝𝑖 2 Also find the unbiased estimator of variance.
- 43. Unordered Estimator (H-T Estimator) • Inclusion probability calculation • Define unbiased estimator of total • Its variance Theorem 5.9.1