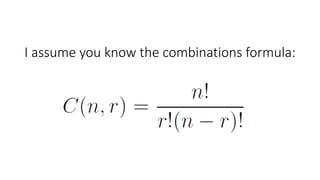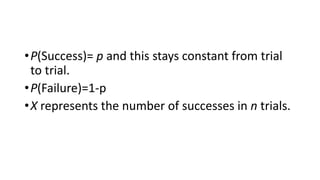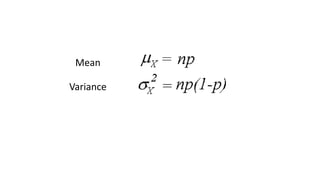The document discusses the binomial distribution and its properties. The binomial distribution describes the number of successes in a fixed number of independent yes/no experiments where the probability of success is constant for each trial. It provides examples of calculating the probability of getting a certain number of successes, such as getting heads at least 60 times in 100 coin flips or winning a cash prize exactly twice in 4 lottery tickets.

1. Binomial Distribution

2. I assume you know the combinations formula:

3. A coin is flipped 100 times.
What is the probability heads comes up at
least 60 times?

4. You buy a certain type of lottery ticket once a
week for 4 weeks.
What is the probability you win a cash prize
exactly twice?

5. The number of successes in n independent
Bernoulli trials has a binomial distribution.
Bernoulli trial is a random experiment with exactly two
possible outcomes, "success" and "failure“.

6. •P(Success)= p and this stays constant from trial
to trial.
•P(Failure)=1-p
•X represents the number of successes in n trials.

7. Then X has a binomial distribution:
For x=0,1,2,…,n

8. Mean
Variance

9. Example:
A six-sided die is rolled 3 times.
What is the probability a 5 come up exactly twice?
Success: Rolling a 5
Failure: Rolling anything but not a 5

10. Let X represent the number of fives in 3 rolls
X has a binomial distribution with n=3 and p=1/6
𝑃 𝑥 = 2 = (
3
2
)
1
6
2
(1 −
1
6
)3−2
=0.0694

11. 1
2
2
3
3
3
3
S
S
S
S
S
S
S
F
F
F
F
F
F
F
SSSSSS
SSF
SFS
SFF
FSS
FSF
FFS
FFF
Exact 3 success
occur in those 3
sequence
𝑝 𝑥 = 2 = 3𝑝2
(1 − 𝑝)1
3
2
= 3

12. Thank you