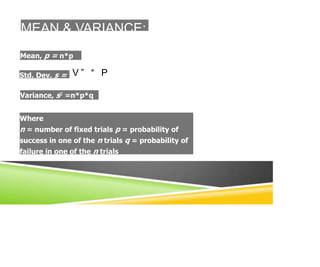
The document discusses the binomial probability distribution, which describes experiments with a fixed number of trials where each trial results in success or failure. The key properties are that the probability of success (p) is constant across trials and trials are independent. Examples show how to calculate the probability of different numbers of successes using the binomial distribution formula. Applications include clinical trials, personality assessments, and quality control.

1. BINOMIAL
PROBABILITY
DISTRIBUTION

2. BASICS & TERMINOLOGY:
> Outcome:- The end result of an experiment.
> Random experiment
predictable.
> Random Event:- A
Experiments whose outcomes are not
random event is an outcome or set of
outcomes of a random experiment that share a common attribute.
> Sample space:- The sample space is an exhaustive list of all the
possible outcomes of an experiment, which is usually denoted

3. > Random Variables.
□ Discrete Random Variable .
□ Continuous Random Variable.
> Bernoulli Trial:
A trial having only two possible outcomes is
called Bernoulli trials.
example:
□ success or failure
□ head or tail

4. > Binomial Distribution:-
The Binomial Distribution describes discrete , not
continuous, data, resulting from an experiment known as
Bernoulli process.

5. A binomial experiment is one that
possesses the following properties:
► The experiment consists of n repeated trials;
► Each trial results in an outcome that may be classified as a success or
a failure (hence the name, binomial);
► The probability of a success, denoted by p, remains constant from trial
to trial and repeated trials are independent.
► The number of successes X in n trials of a binomial experiment is
called a binomial random variable.
► The probability distribution of the random variable X is called a
binomial distribution, and is given by the formula:
P(X) = Cn
xpxqn-x

6. EXAMPLE 1
A die is tossed 3 times. What is the probability of
(a) No fives turning up?
(b) 1 five?
(c) 3 fives?

7. This is a binomial distribution because there are only 2 possible outcomes (we get a 5
or we don’t).
Now,;/ = 3 for each part. Let A" = number of fives appearing.
(a) Here, Y = 0.
P(X= 0) = cip'q-* = Co(i)°(f) = 2ll = ° 5787
(b) Here, x= 1.
^(Y- 1) = Clp'q”-* - C?(-J-)1(-|)2 ~ JY6 ~ 0.34722
(c) Here, .v = 3.
3 0
P(Y= 3) = C”xp*q"~* = C | ( i ) ( - J ) ' = 2 1 6 = 4 . 6296 x 10"3

8. EXAMPLE 2:
► Hospital records show that of patients suffering from a
certain disease, 75% die of it. What is the probability that
of 6 randomly selected patients, 4 will recover?

9. This is a binomial distribution because there are only 2
outcomes (the patient dies, or does not).
Let X = number who recover.
Here, // = 6 and ,v = 4. Letp = 0.25 (success - i.e. they live), <y
= 0.75 (failure, i.e. they die).
The probability that 4 will recover:
PLY) =
= C6
a(
0.25)4(0.75)2 =
15x 2.1973
xlO“3
0.0329595

10. EXAMPLE 3:
In the old days, there was a probability of 0.8 of success in
any attempt to make a telephone call.
(This often depended on the importance of the person
making the call, or the operator's curiosity!)
Calculate the probability of having 7 successes in 10
attempts.

11. Probability of success p = 0.8,
so q- 0.2. X=success in
getting through.
Probability of 7 successes in
10 attempts:
Probability = P(X = 7)
= Cj°(0.8)7 (0.2)10-7 = 0.20133

13. EXAMPLE 4:
The ratio of boys to girls at birth in Singapore is quite high at
1.09:1.
What proportion of Singapore families with exactly 6 children
will have at least 3 boys?
(Ignore the probability of multiple births.)
[Interesting and disturbing trivia: In most countries the
ratio of boys to girls is about 1.04:1, but in China it is
1.15:1.]

14. he probability of getting a boy is j QQ — 0. 521 5
et X = number of boys in the family
ere,
n = 6 ,
p = 0 5215,
<7 = 1 - 0 52153 = 0 4785
- 3 P(X) - Cn
xp*q- C|(0.5215)3(0.4785)3 - 0.31077
- 4 P(X) - C5(0.5215)4(0.4785)2 - 0.25402
- 5 P(X) - Cf(0.5215)5(0.4785)1 - 0. 1 1074
- 6 P(X) - C|(0.5215)6 (0.4785)° - 2. 0 1 1 5 x 10'2
o the probability of getting at least 3 boys is:
Probability = P(X >3)
- 0.31077+0.25402 + 0. 11074 + 2. Oil 5x 102
- 0.69565
NOTE: We could have calculated it like this:
P{X > 3) - 1 - (PC*0) + P(*,) + P(*2))

15. EXAMPLE 5:
A manufacturer of metal pistons finds that on the average, 12% of his
pistons are rejected because they are either oversize or undersize. What
is the probability that a batch of 10 pistons will contain
(a) no more than 2 rejects?
(b) (b) at least 2 rejects?

16. Let X = number of rejected pistons (In this case,
"success” means rejection!)
Here, n = 10, p = 0.12, q = 0.88.
(a)
No rejects
x - 0 P(X) - C”p*q*~x - cj°(0. 12)0(0.88)'°
One reject
AT - 1 P(X) - C|°(0. 12)'(0.88)® - 0.37977 Two rejects
x - 2 P(X) - Cj°(0. I2)2(0. 88)S - 0.23304 So the probability
of getting no more than 2 rejects is:
Probability = P(X < 2)
= 0.278 5+ 0.3 797 7 4-0.233 04

17. ptoceed 3$ Mows.
probabilityofatleast 2 reject*
.t-(PW+PW)
3 -(0W+0.3WT)
- 0.24H2

18. BINOMIAL FREQUENCY DISTRIBUTION
► If the binomial probability distribution is multiplied by
the number of experiment N then the distribution is
called binomial frequency distribution.
f(X=x)= N P(X=x)=N
v.
n
x
qn x px

19. MEAN & VARIANCE:
Mean, p = n*p
Std. Dev. s = V ” * P
Variance, s2 =n*p*q
Where
n = number of fixed trials p = probability of
success in one of the n trials q = probability of
failure in one of the n trials

20. Applications for binomial distributions
> Binomial distributions describe the possible number of times that a
particular event will occur in a sequence of observations.
> They are used when we want to know about the occurrence of an
event, not its magnitude.
Example:
> In a clinical trial, a patient’s condition may improve or not. We study
the number of patients who improved, not how much better they feel.
> Is a person ambitious or not? The binomial distribution describes the
number of ambitious persons, not how ambitious they are.
> In quality control we assess the number of defective items in a lot
^^iaaQds,irrespective of the type of defect.