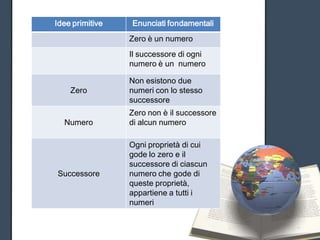
Il documento analizza il contributo di Bertrand Russell e Gottlob Frege nell'indagine sui fondamenti della matematica durante la seconda rivoluzione scientifica. Russell identifica antinomie, come il paradosso del barbiere, nel tentativo di sviluppare un sistema logico coerente, culminando nella proposta della teoria dei tipi insieme a Whitehead per evitare contraddizioni. Tuttavia, il problema delle antinomie rimane aperto, con Kurt Gödel che successivamente mette in dubbio l'autoconsistenza dei sistemi formali.

1. Bertrand Russell
(Trellech, 1872 – Penrhyndeudraeth, 1970)

2. « Il problema dell'umanità è che
gli sciocchi e i fanatici sono
estremamente sicuri di loro
stessi, mentre le persone più
sagge sono piene di dubbi. »

3. Uno dei tratti caratterizzanti la
seconda rivoluzione scientifica è
l’indagine sui fondamenti della
matematica, indagine che ha nel
tedesco Frege e nel britannico
Russell i massimi esponenti.

4. Russell
Frege

5. Per Frege tutti i concetti aritmetici
sono definibili da un punto di vista
logico, in termini di classi o insiemi.
La logica viene quindi vista come la
base della matematica.

6. Il logicismo viene però messo
in crisi da Bertrand Russell che
determina la cosiddetta crisi dei
fondamenti della matematica.

7. Nello sviluppo del pensiero di
Russell fondamentale è l’incontro
con Peano, autore di un sistema di
notazione simbolica ancor oggi in
uso, che ha mostrato la possibilità di
ridurre algebra e aritmetica classiche
a pochi fondamentali principi.

8. Peano

9. Secondo Peano aritmetica e algebra
possono essere derivate da cinque
enunciati fondamentali e da tre idee
primitive.

10. Idee primitive Enunciati fondamentali
Zero è un numero
Il successore di ogni
numero è un numero
Non esistono due
Zero numeri con lo stesso
successore
Zero non è il successore
Numero di alcun numero
Ogni proprietà di cui
gode lo zero e il
successore di ciascun
Successore numero che gode di
queste proprietà,
appartiene a tutti i
numeri

11. Alla luce delle ricerche di Peano,
Russell tenta di dimostrare che
qualsiasi asserzione sui numeri
naturali è sostituibile da un’altra
asserzione che non nomina numeri
naturali ma classi.

12. In questo suo tentativo Russell
finisce per incontrare la
riflessione di Frege che aveva
definito i numeri naturali come
classe di classi, per cui il numero
2 altro non sarebbe che la classe
di tutte le coppie.

13. Proprio sull’ipotesi fregeana
di classe Russell, che pure
concorda con molte delle tesi
del logico tedesco, si imbatte
in un’antinomia.

14. Esistono classi,
osserva Russell, che
non contengono se
stesse come elemento
e classi invece che
contengono se stesse.
Le prime possono
definirsi irregolari, le
seconde regolari.

15. Siamo di fronte al
famoso paradosso del
barbiere o, è la stessa
cosa, al più antico
paradosso del mentitore.

16. “ In un villaggio c’è un solo barbiere
che rade tutti, e soltanto, gli uomini
che non si radono da soli. Chi rade il
barbiere?”

17. Il barbiere rade se stesso, ma ciò
non è possibile poiché il barbiere
rade solo quelli che non si radono da
soli.

18. Il barbiere non rade se stesso, ma
ciò non è possibile poiché il barbiere
rade tutti quelli che non si radono da
sé e quindi dovrebbe radere anche
se stesso.

19. Comunque si affronti la questione ci si
trova di fronte ad una contraddizione.
Il problema è identico nel paradosso
del mentitore: “Epimenide cretese
dice che tutti i cretesi mentono”.
Non è difficile realizzare che se
Epimenide dice il vero mente, e
viceversa se mente dice la verità.

20. Detto in altri termini:
la classe A di tutte e solo
quelle classi che non sono
elemento di se stesse
(ovvero la classe di tutte le
classi regolari) è una classe
regolare o irregolare?
Ovvero appartiene o meno a
se stessa?

22. Se la classe A non appartiene a se
stessa deve necessariamente
appartenervi in quanto è la classe di
tutte le classi che non contengono se
stesse.
Se A appartiene invece a se tessa,
allora non può assolutamente
appartenervi, in quanto è la classe
che comprende solo le classi che
non hanno se stesse come
elemento. Quindi appartiene a se
stessa solo se non appartiene a se
stessa.

23. Comunque si voglia girare la
questione ci troviamo di fronte ad
un’evidente contraddizione (come
comprese subito Frege che cambiò la
direzione dei suoi studi).
Tuttavia Russell ritiene sia possibile
trovare una soluzione logicamente
valida.

24. Insieme a Whitehead,
Russell propone la
cosiddetta teoria dei tipi,
partendo dal presupposto
che si possa costruire un
sistema esente da
contraddizioni eliminando
le classi che comprendono
se stesse come elementi.

25. Whitehead

26. Questa teoria prevede che vi siano vari tipi di oggetti
Individui Oggetti di tipo 0
Classi di oggetti di tipo 0 Oggetti di tipo 1
Classi di oggetti di tipo 1 Oggetti di tipo 2
Classi di oggetti di tipo n-1 Oggetti di tipo n

27. Gli studenti, per esempio, essendo
individui sono elementi di tipo 0.
La classe scolastica è un oggetto di
tipo 1, in quanto costituita di
elementi di tipo 0.
La scuola è un oggetto di tipo 2, in
quanto comprende elementi di tipo
1.

28. Infatti, per continuare con l’esempio, un insieme
di studenti non è uno studente; un insieme di
classi non è una classe; un insieme di scuole
non è una scuola.

30. Russell
La regola può anche essere espressa così:
un oggetto di tipo n è composto
esclusivamente di elementi di tipo n-1 e
quindi non può contenere se stesso.
In tal modo l’antinomia sarebbe eliminata.

31. Sulla base della teoria dei tipi, Russell e
Whitehead ritengono di poter riprendere il
progetto logicista.
In realtà il problema resta aperto, perché
se da un lato vengono introdotti nuovi
principi logici, come l’assioma dell’infinito
che tuttavia rinvia a elementi extralogici,
dall’altro non si può escludere la comparsa
di nuove antinomie.
Spetterà a Kurt Godel suggerire nuove
soluzioni, che tuttavia sembrano
ridimensionare in via definitiva le
pretese di autoconsistenza dei
sistemi formalizzati.

33. Pietro Volpones - 2011