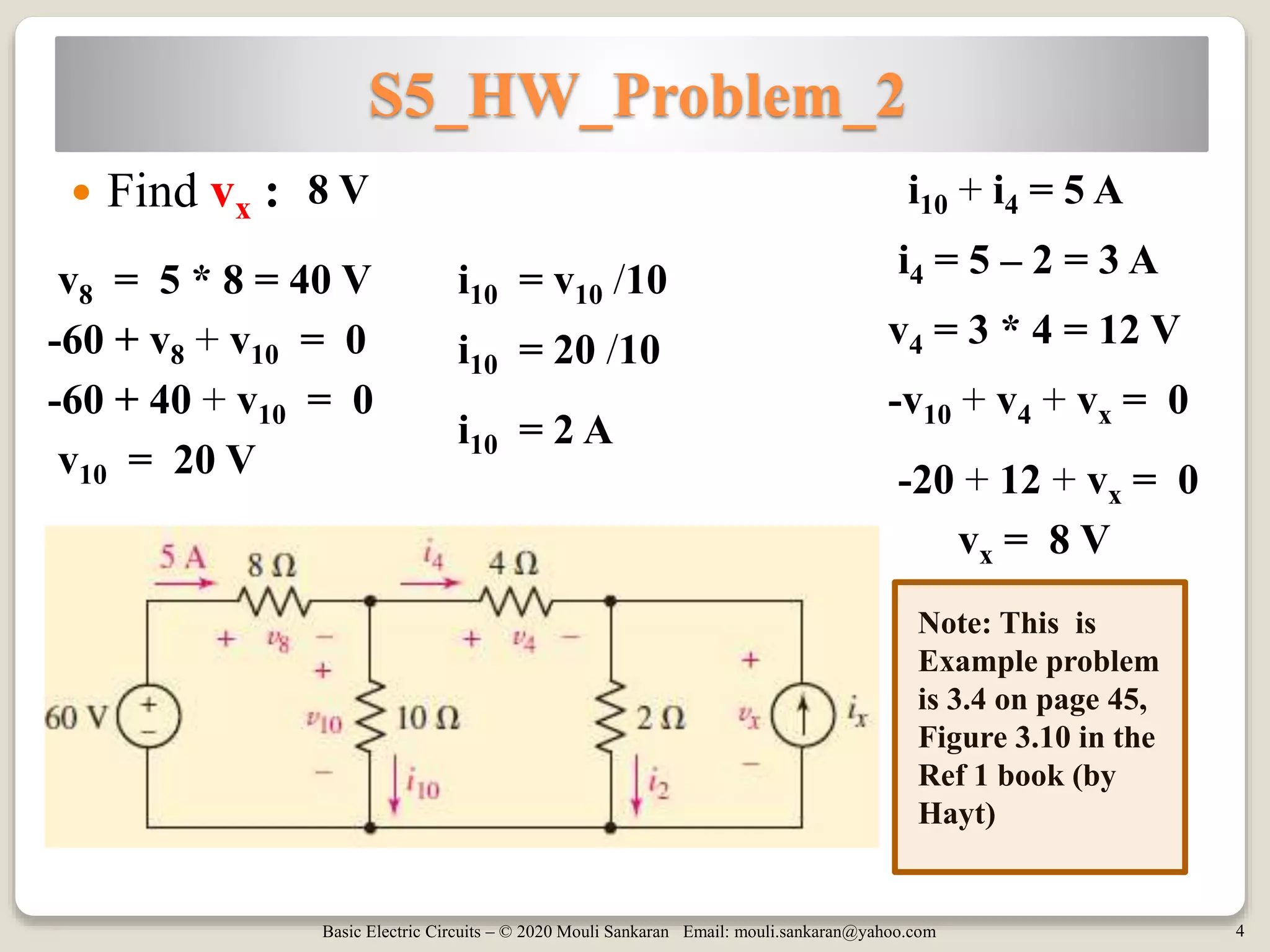
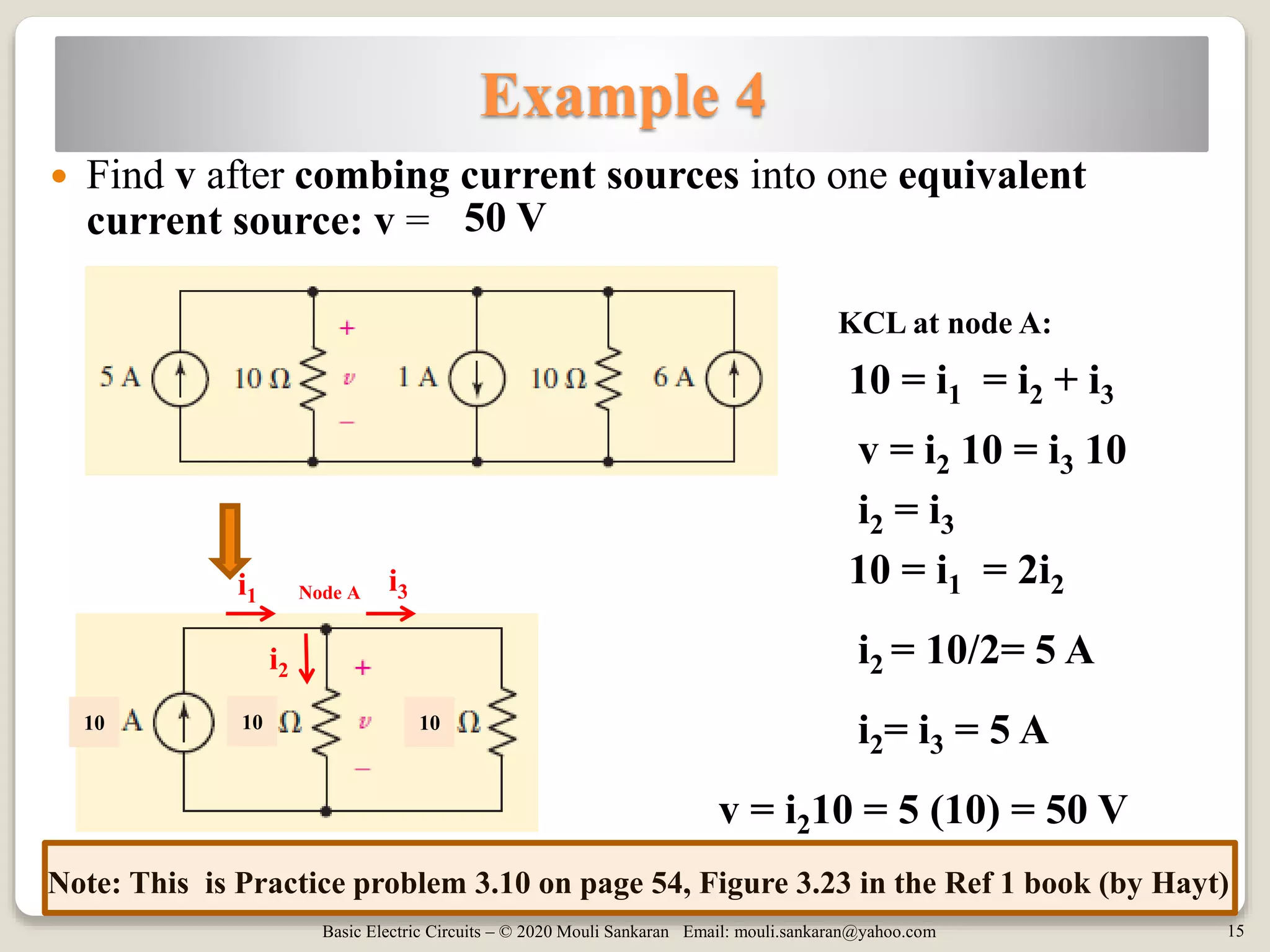
The document covers advanced concepts in basic electric circuits, focusing on Kirchhoff's Voltage Law (KVL) problems, circuit simplification techniques, and the methods for combining voltage and current sources in series and parallel. It includes several example problems illustrating these concepts and emphasizes the distinction between independent and dependent sources during simplification. The final session summarizes the key topics discussed throughout the document.