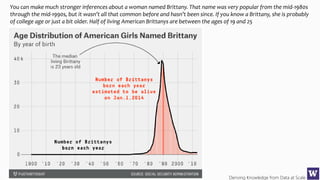
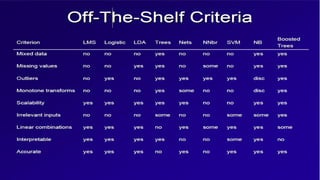
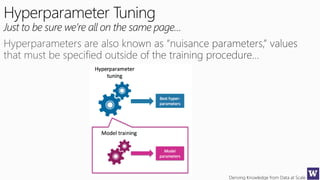
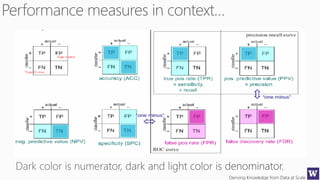
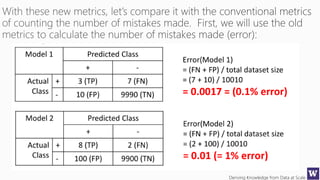
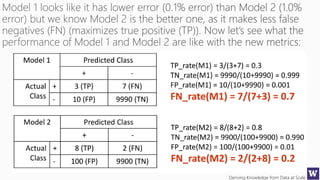
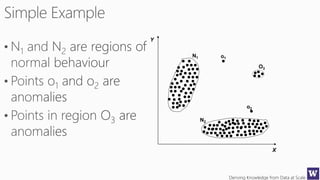
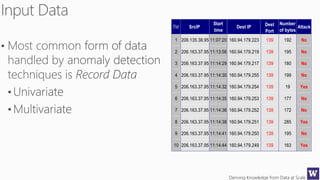
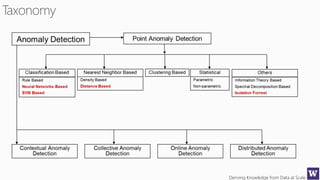
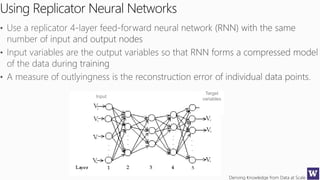
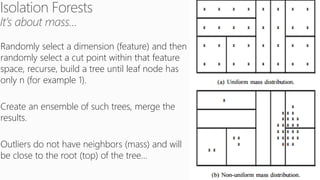
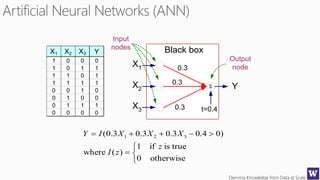
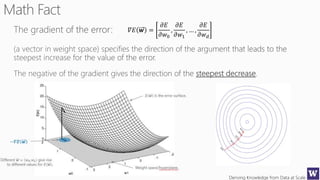
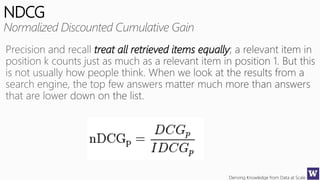The document discusses various machine learning concepts like model overfitting, underfitting, missing values, stratification, feature selection, and incremental model building. It also discusses techniques for dealing with overfitting and underfitting like adding regularization. Feature engineering techniques like feature selection and creation are important preprocessing steps. Evaluation metrics like precision, recall, F1 score and NDCG are discussed for classification and ranking problems. The document emphasizes the importance of feature engineering and proper model evaluation.