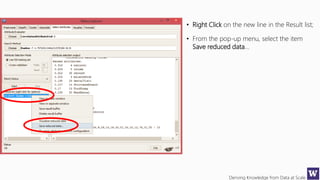
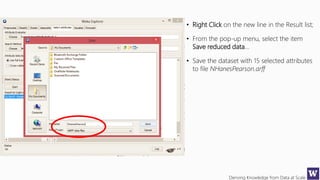
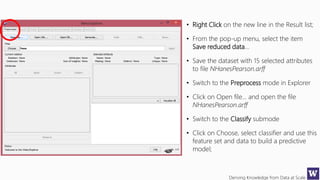
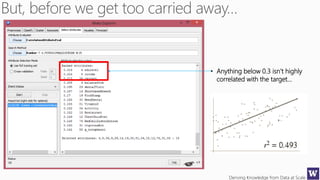
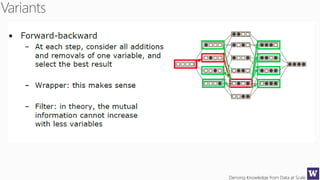
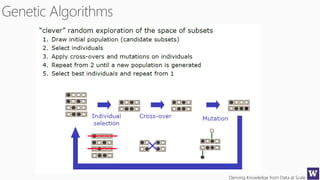
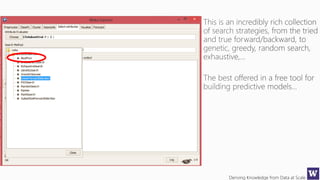
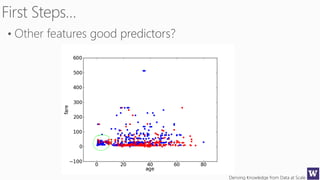
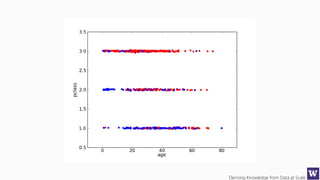
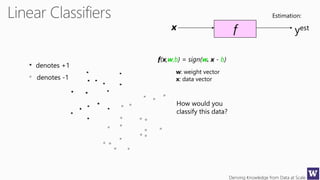
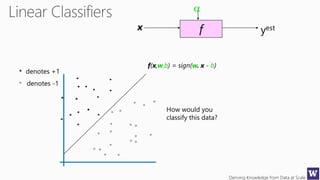
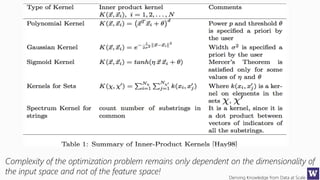
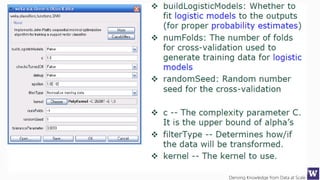
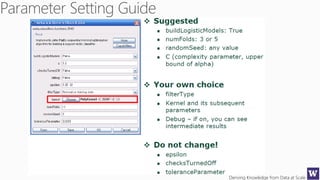
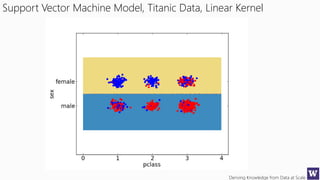
This document appears to be lecture slides for a course on deriving knowledge from data at scale. It covers many topics related to building machine learning models including data preparation, feature selection, classification algorithms like decision trees and support vector machines, and model evaluation. It provides examples applying these techniques to a Titanic passenger dataset to predict survival. It emphasizes the importance of data wrangling and discusses various feature selection methods.








































































![Deriving Knowledge from Data at Scale
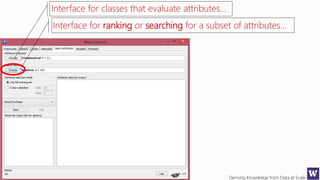
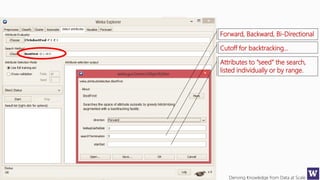
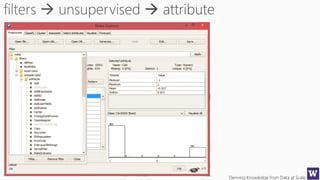
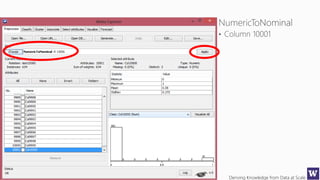
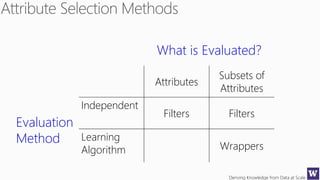
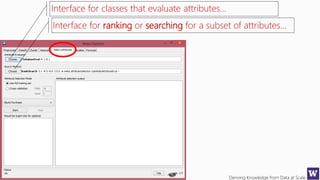
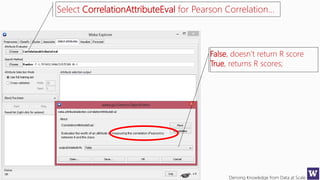
Ranks attributes by their individual evaluations, used in
conjunction with GainRatio, Entropy, Pearson, etc…
Number of attributes to return,
-1 returns all ranked attributes;
Attributes to ignore (skip) in the
evaluation forma: [1, 3-5, 10];
Cutoff at which attributes can
be discarded, -1 no cutoff;](https://image.slidesharecdn.com/bargauwdatasciencelecture7-160424211637/85/Barga-Data-Science-lecture-7-119-320.jpg)