Sara Hooker, profile picture
Uploaded bySara Hooker
PDF, PPTX2,198 views

Module 5: Decision Trees

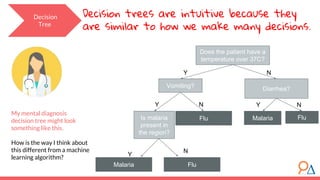
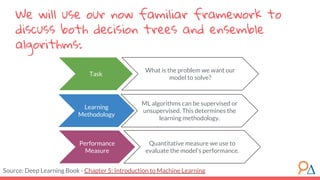
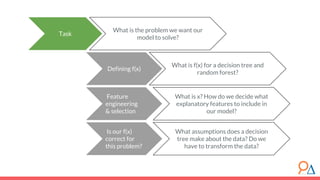
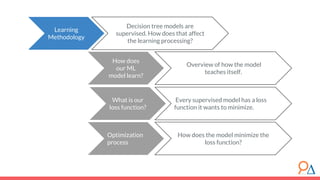
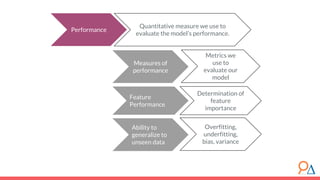
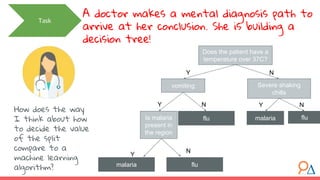
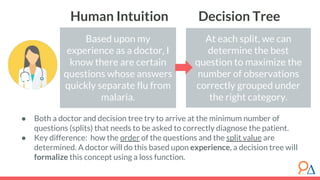
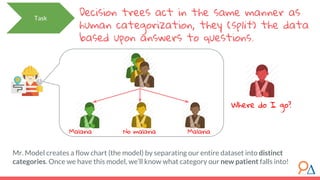
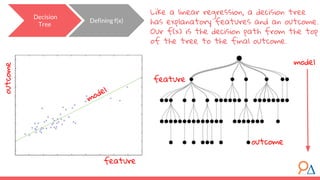
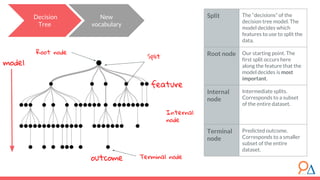
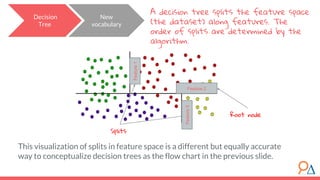
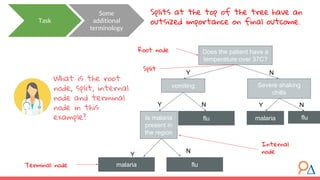
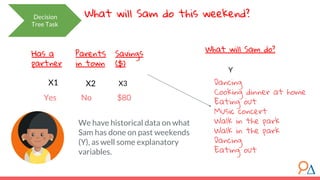
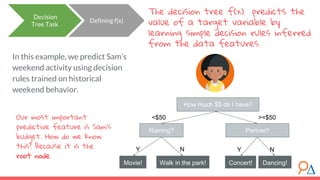
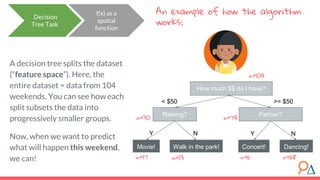
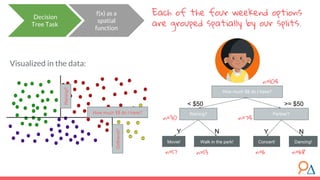
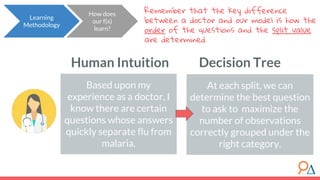
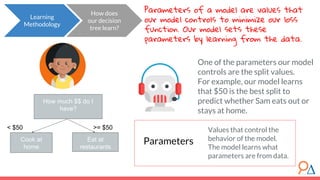
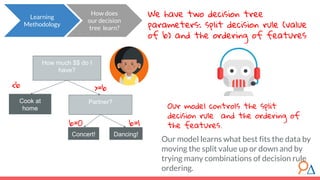
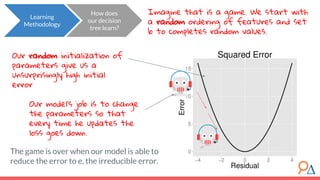
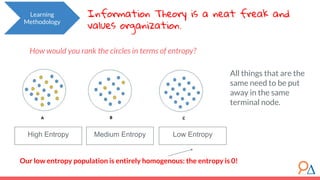
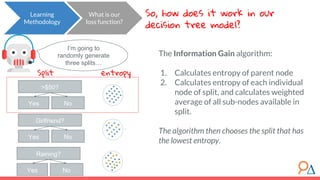
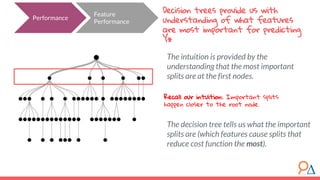
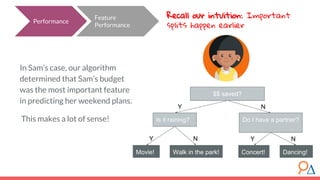
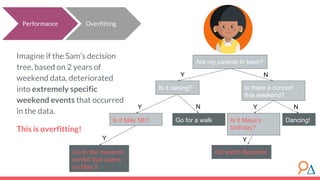
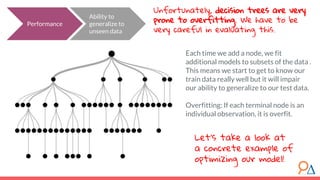
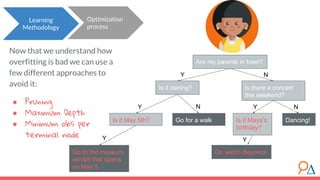
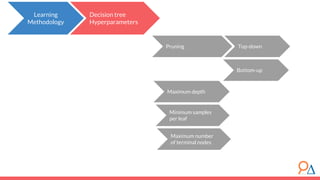
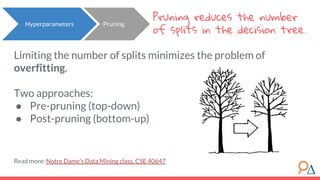
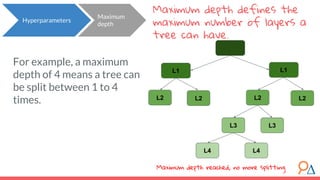
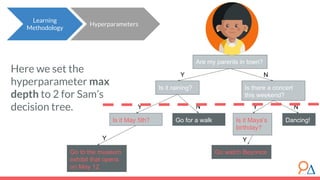
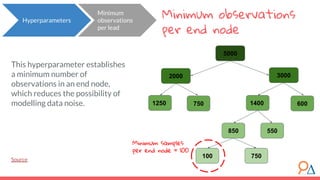
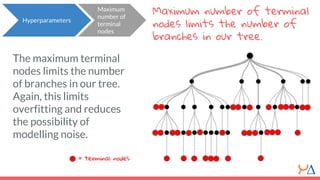
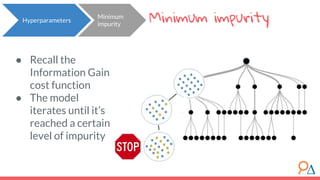
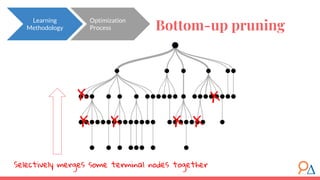
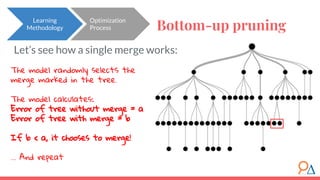
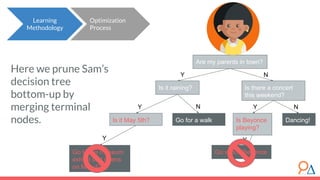
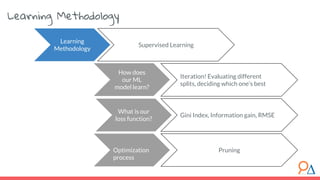
This document discusses decision trees as a machine learning algorithm used for classification and regression tasks. It explains the structure of decision trees, their intuitive similarity to human decision-making, and the learning methodology, which involves optimizing splits based on loss functions like Gini impurity and mean squared error. The content also highlights the pros and cons of decision trees, such as their susceptibility to overfitting and their interpretability.

Embed presentation

Download as PDF, PPTX
Decision Trees
This course content is being actively developed by Delta Analytics, a 501(c)3 Bay Area nonprofit that aims to empower communities to leverage their data for good. Please reach out with any questions or feedback to inquiry@deltanalytics.org. Find out more about our mission here. Delta Analytics builds technical capacity around the world.
Module 5: Decision trees
❏ Decision trees ❏ Intuition ❏ The “best” split ❏ Model performance ❏ Model optimization (pruning) Module Checklist:
Where are we? We’ve laid much of the groundwork for machine learning, and introduced our very first algorithm of linear regression. Now, we can focus on expanding our algorithm toolkit. Decision trees are another type of algorithm that can accomplish the same objective of prediction that linear regression can. We will also go deeper into the pros and cons of decision trees in this module.
Where are we? Supervised Algorithms Let’s do a quick intro to decision trees and ensembles! Linear regression Decision tree Ensemble Algorithms
Decision Tree Today, we will start by looking at a decision tree algorithm. A decision tree is a set of rules we can use to classify data into categories (also can be used for regression tasks). Humans often use a similar approach to arrive at a conclusion. For example, doctors ask a series of questions to diagnose a disease. A doctor’s goal is to ask the minimum number of questions needed to arrive at the correct diagnosis. What is wrong with my patient? Help me put together some questions I can use to diagnose patients correctly.
Decision Tree Decision trees are intuitive because they are similar to how we make many decisions. My mental diagnosis decision tree might look something like this. How is the way I think about this different from a machine learning algorithm? Does the patient have a temperature over 37C? Vomiting? Diarrhea? NY Malaria FluFluIs malaria present in the region? Y Y NN FluMalaria N Y
Decision Tree Decision trees are intuitive and can handle more complex relationships than linear regression can. A linear regression is a single global trend line. This makes it inflexible for more sophisticated relationships. Sources: https://www.slideshare.net/ANITALOKITA/winnow-vs-perceptron, http://www.turingfinance.com/regression-analysis-using-python-sta tsmodels-and-quandl/
We will use our now familiar framework to discuss both decision trees and ensemble algorithms: Task What is the problem we want our model to solve? Performance Measure Quantitative measure we use to evaluate the model’s performance. Learning Methodology ML algorithms can be supervised or unsupervised. This determines the learning methodology. Source: Deep Learning Book - Chapter 5: Introduction to Machine Learning
Task What is the problem we want our model to solve? Defining f(x) What is f(x) for a decision tree and random forest? Feature engineering & selection What is x? How do we decide what explanatory features to include in our model? What assumptions does a decision tree make about the data? Do we have to transform the data? Is our f(x) correct for this problem?
Learning Methodology Decision tree models are supervised. How does that affect the learning processing? What is our loss function? Every supervised model has a loss function it wants to minimize. Optimization process How does the model minimize the loss function? How does our ML model learn? Overview of how the model teaches itself.
Performance Quantitative measure we use to evaluate the model’s performance. Measures of performance Metrics we use to evaluate our model Feature Performance Determination of feature importance Overfitting, underfitting, bias, variance Ability to generalize to unseen data
Decision Tree
Decision tree: model cheat sheet ● Susceptible to overfitting (poor performance on test set) ● High variance between data sets ● Can become unstable: small variations in the training data result in completely different trees being generated ● Mimics human intuition closely (we make decisions in the same way!) ● Not prescriptive (i.e., decision trees do not assume a normal distribution) ● Can be intuitively understood and interpreted as a flow chart, or a division of feature space. ● Can handle nonlinear data (no need to transform data) Pros Cons
Task
Task How does a doctor diagnose her patients based on their symptoms? What are we predicting?
Task A doctor builds a diagnosis from your symptoms. I start by asking patients a series of questions about their symptoms. I use that information to build a diagnosis. Flu Malaria Flu Flu diagnosis Yes No No Yes Severe Severe Mild None Shaking chills vomitingtemp X1 X2 X3 Y Y* 39.5°C 37.8°C 37.2°C 37.2°C predicted diagnosis Flu Malaria Malaria Flu There are some questions the doctor does not need to ask because she learns it from her environment. (For example, a doctor would know if malaria present in this region.) A machine, however, would have to be explicitly taught this feature.
Task A doctor makes a mental diagnosis path to arrive at her conclusion. She is building a decision tree! How does the way I think about how to decide the value of the split compare to a machine learning algorithm? Does the patient have a temperature over 37C? vomiting Severe shaking chills NY malaria flufluIs malaria present in the region Y Y NN flumalaria N Y
At each split, we can determine the best question to maximize the number of observations correctly grouped under the right category. ● Both a doctor and decision tree try to arrive at the minimum number of questions (splits) that needs to be asked to correctly diagnose the patient. ● Key difference: how the order of the questions and the split value are determined. A doctor will do this based upon experience, a decision tree will formalize this concept using a loss function. Based upon my experience as a doctor, I know there are certain questions whose answers quickly separate flu from malaria. Human Intuition Decision Tree
To determine whether a new patient has malaria, a doctor uses her experience and education, and machine learning creates a model using data. By using a machine learning model, our doctor is able to use both her experience and data to make the best decision! Machine learning adds the power of data to our doctor’s task. Task
Mr. Model creates a flow chart (the model) by separating our entire dataset into distinct categories. Once we have this model, we’ll know what category our new patient falls into! Decision trees act in the same manner as human categorization, they (split) the data based upon answers to questions. Where do I go? Malaria MalariaNo malaria Task
To get a sense of how this “splitting” works, let’s play a guessing game. I am thinking of something that is blue. You may ask 10 questions to guess what it is.
The first few questions you would probably ask may include: - Is it alive? (No) - Is it in nature? (Yes)
Then, as you got closer to the answer, your questions would become more specific. - Is it solid or liquid? (Liquid) - Is it the ocean? (Yes!)
Some winning strategies include: ● Use questions early on that eliminate the most possibilities. ● Questions often start broad and become more granular. This process is your mental decision tree. In fact, this strategy captures many of the qualities of our algorithm!
You created your own decision tree based on your own experience of what you know is blue to make an educated guess as to what I was thinking of (the ocean). Similarly, a decision tree model will make an educated guess, but instead of using experience, it uses data. Now, let’s build a formal vocabulary for discussing decision trees.
Like a linear regression, a decision tree has explanatory features and an outcome. Our f(x) is the decision path from the top of the tree to the final outcome. feature feature outcome outcome model model Decision Tree Defining f(x)
feature outcome model Decision Tree New vocabulary Internal node Terminal node Split Split The “decisions” of the decision tree model. The model decides which features to use to split the data. Root node Our starting point. The first split occurs here along the feature that the model decides is most important. Internal node Intermediate splits. Corresponds to a subset of the entire dataset. Terminal node Predicted outcome. Corresponds to a smaller subset of the entire dataset. Root node
Decision Tree New vocabulary Splits Root node Feature 2 Feature1 Feature3 This visualization of splits in feature space is a different but equally accurate way to conceptualize decision trees as the flow chart in the previous slide. A decision tree splits the feature space (the dataset) along features. The order of splits are determined by the algorithm.
Task Splits at the top of the tree have an outsized importance on final outcome. What is the root node, split, internal node and terminal node in this example? Does the patient have a temperature over 37C? vomiting Severe shaking chills NY malaria flufluIs malaria present in the region Y Y NN flumalaria N Y Some additional terminology Internal node Terminal node Split Root node
Decision Tree Let’s look at another question to combine our intuition with formal vocabulary. What should Sam do this weekend? Let’s get this weekend started! Dancing Cooking dinner at home Eating at fancy restaurant Music concert Walk in the park Y = Choice of weekend activity Training data set: You have a dataset of what she has done every weekend for the last two years. Defining f(x)
Decision Tree Task What will Sam do this weekend? Dancing Cooking dinner at home Eating out Music concert Walk in the park Walk in the park Dancing Eating out Y What will Sam do? $80No Savings ($) X2 Parents in town Has a partner Yes X3X1 We have historical data on what Sam has done on past weekends (Y), as well some explanatory variables.
In this example, we predict Sam’s weekend activity using decision rules trained on historical weekend behavior. How much $$ do I have? Raining? Partner? >=$50<$50 Concert! Dancing!Walk in the park!Movie! Y Y NN Decision Tree Task Defining f(x) The decision tree f(x) predicts the value of a target variable by learning simple decision rules inferred from the data features. Our most important predictive feature is Sam’s budget. How do we know this? Because it is the root node.
A decision tree splits the dataset (“feature space”). Here, the entire dataset = data from 104 weekends. You can see how each split subsets the data into progressively smaller groups. Now, when we want to predict what will happen this weekend, we can! How much $$ do I have? Raining? Partner? < $50 Concert! Dancing!Walk in the park!Movie! Y Y NN Decision Tree Task f(x) as a spatial function >= $50 n=104 n=17 n=30 n=74 n=6n=13 An example of how the algorithm works: n=68
How much $$ do I have? Raining? Partner? < $50 Concert! Dancing!Walk in the park!Movie! Y Y NN Decision Tree Task f(x) as a spatial function >= $50 n=104 n=17 n=30 n=74 n=6n=13 Each of the four weekend options are grouped spatially by our splits. n=68 Visualized in the data: How much $$ do I have? Raining? Girlfriend?
Now we understand the mechanics of the decision tree task. But how does a decision tree learn? How does it know where to split the data, and in what order? We turn now to examine decision trees’ learning methodology.
Learning Methodology
At each split, we can determine the best question to ask to maximize the number of observations correctly grouped under the right category. Based upon my experience as a doctor, I know there are certain questions whose answers quickly separate flu from malaria. Remember that the key difference between a doctor and our model is how the order of the questions and the split value are determined. Human Intuition Decision Tree Learning Methodology How does our f(x) learn?
key difference between a doctor and our model is how the order of the questions and the split value are determined. Learning Methodology How does our f(x) learn? The two key levers that can be changed to improve accuracy of our medical diagnosis are: - The order of the questions - The split value at each node. (For example the temperature boundary) A doctor will make these decisions based upon experience, a decision tree will set these parameters to minimize our loss function by learning from the data.
Recap: Loss function Linear Regression A loss function quantifies how unhappy you would be if you used f(x) to predict Y* when the correct output is y. It is the object we want to minimize. Remember: All supervised models have a loss function (sometimes also known as the cost function) they must optimize by changing the model parameters to minimize this function. Sound familiar? We just went over a similar optimization process for linear regression (our loss function there was MSE). Source: Stanford ML Lecture 1
Values that control the behavior of the model. The model learns what parameters are from data. Parameters How does our decision tree learn? Parameters of a model are values that our model controls to minimize our loss function. Our model sets these parameters by learning from the data. Learning Methodology One of the parameters our model controls are the split values. For example, our model learns that $50 is the best split to predict whether Sam eats out or stays at home. How much $$ do I have? Cook at home Eat at restaurants < $50 >= $50
How does our decision tree learn? We have two decision tree parameters: split decision rule (value of b) and the ordering of features Learning Methodology >=b How much $$ do I have? Cook at home <b Partner? Concert! Dancing! b=0 b=1 Our model controls the split decision rule and the ordering of the features. Our model learns what best fits the data by moving the split value up or down and by trying many combinations of decision rule ordering.
Central problem: How do we learn the “best” split?
How does our decision tree learn? There are so many possible decision paths and split values - in fact, an infinite amount! How does our model choose? Learning Methodology >=b How much $$ do I have? Cook at home <b Partner? Concert! Dancing! b=0 b=1 Our model checks the parameter choices against the loss function every time it makes a change. It checks whether the error went up, down or stayed the same. If it went down, our model knows it did something right! Oh no! That made it worse. Let’s try something else.
Our random initialization of parameters give us a unsurprisingly high initial error How does our decision tree learn? Imagine that is a game. We start with a random ordering of features and set b to completes random values. Learning Methodology Our model’s job is to change the parameters so that every time he updates the loss goes down. The game is over when our model is able to reduce the error to e, the irreducible error.
Regression Classification Continuous variable Categorical variable A classification problem is when are trying to predict whether something belongs to a category, such as “red” or “blue” or “disease” and “no disease”. A regression problem is when we are trying to predict a numerical value given some input, such as “dollars” or “weight”. Source: Andrew Ng , Stanford CS229 Machine Learning Course Decision trees also can be used for two types of tasks! Recap of tasks:
What is our loss function? Our decision tree loss function depends on the type of task. Learning Methodology I can minimize all types of loss functions! The most common loss functions for decision trees include: For classification trees: 1. Gini Impurity 2. Entropy For regression trees: 3. Mean Squared Error For example, the loss function for a regression decision tree should feel familiar. It is the same loss function we used for linear regression!
Information gain attempts to minimize entropy in each subnode. Entropy is defined as a degree of disorganization. If the sample is completely homogeneous, then the entropy is zero. If the sample is an equally divided (50% – 50%), it has entropy of one. Learning Methodology For classification trees, we can use information gain! How would you rank the entropy of these circles? Source
All things that are the same need to be put away in the same terminal node. Learning Methodology Information Theory is a neat freak and values organization. How would you rank the circles in terms of entropy? Low EntropyHigh Entropy Medium Entropy Our low entropy population is entirely homogenous: the entropy is 0!
The Information Gain algorithm: 1. Calculates entropy of parent node 2. Calculates entropy of each individual node of split, and calculates weighted average of all sub-nodes available in split. The algorithm then chooses the split that has the lowest entropy. What is our loss function? Learning Methodology So, how does it work in our decision tree model? I’m going to randomly generate three splits… >$50? Yes No Girlfriend? Yes No Raining? Yes No Split entropy
This may look familiar - look back at our discussion of linear regression! Decision trees also use MSE. The split with lower MSE is selected as the criteria to split the population. What is our loss function? Learning Methodology Regression trees use Mean Squared Error. Y-Y* For every point in our dataset, measure the difference between true Y and predicted Y. ^2 Square each Y-Y* to get the absolute distance, so positive values don’t cancel out negative ones when we sum. Sum Sum across all observations so we get the total error. mean Divide the sum by the number of observations we have.
The RMSE algorithm proceeds by: 1. Calculating variance for each node. 2. Calculating variance for each split as weighted average of each node variance. The algorithm then selects the split that has the lowest variance. What is our loss function? Learning Methodology Regression trees use Mean Squared Error. I’m going to randomly generate three splits… Amount of $ Yes No # of girlfriends Yes No Likelihood of rain Yes No Split RMSE 3.83 7.28 10.3
Model Performance
Decision trees provide us with understanding of what features are most important for predicting Y* Recall our intuition: Important splits happen closer to the root node. The intuition is provided by the understanding that the most important splits are at the first nodes. The decision tree tells us what the important splits are (which features cause splits that reduce cost function the most). Performance Feature Performance
In Sam’s case, our algorithm determined that Sam’s budget was the most important feature in predicting her weekend plans. This makes a lot of sense! $$ saved? Is it raining? Do I have a partner? NY Concert! Dancing!Walk in the park!Movie! Y Y NN Performance Feature Performance Recall our intuition: Important splits happen earlier
Go watch Beyonce Imagine if the Sam’s decision tree, based on 2 years of weekend data, deteriorated into extremely specific weekend events that occurred in the data. This is overfitting! Are my parents in town? Is it raining? Is there a concert this weekend? NY Is it Maya’s birthday? Dancing!Go for a walkIs it May 5th? Y Y NN Go to the museum exhibit that opens on May 5 Y Y Performance Overfitting
Performance Ability to generalize to unseen data Our goal in evaluating performance is to find a sweet spot between overfitting and underfitting. If our train data set overfits, it will not generalize to our test set (unseen data) well. However, if it underfits, we are not capturing the complexity of the relationship and our loss will be high! Underfit Overfit Sweet spot Remember that the most important goal we have is to build a model that will generalize well to unseen data.
Each time we add a node, we fit additional models to subsets of the data . This means we start to get to know our train data really well but it will impair our ability to generalize to our test data. Overfitting: If each terminal node is an individual observation, it is overfit. Performance Ability to generalize to unseen data Let’s take a look at a concrete example of optimizing our model! Unfortunately, decision trees are very prone to overfitting. We have to be very careful in evaluating this.
Model Optimization
Go watch Beyonce Now that we understand how overfitting is bad we can use a few different approaches to avoid it: ● Pruning ● Maximum Depth ● Minimum obs per terminal node Are my parents in town? Is it raining? Is there a concert this weekend? NY Is it Maya’s birthday? Dancing!Go for a walkIs it May 5th? Y Y NN Go to the museum exhibit that opens on May 5 Y Y Learning Methodology Optimization process
Pruning, max depth and n_ obs in a terminal node are all examples of hyperparameters. Learning Methodology Pruning, max depth and n_ obs in a terminal node are all decision tree hyperparameters set before training. Their values are not learned from the data so the model cannot say anything about them. Hyperparameters are higher level settings of a model that are fixed before training begins. You, not the model decide what the hyperparameters are!
● In linear regression, the coefficients were parameters. Y = a + b1 x1 + b2 x2 + … + e ○ Parameters are learned from the training data using the chosen algorithm. ● Hyperparameters cannot be learned from the training process. They express “higher-level” properties of the model such as its complexity or how fast it should learn. Source: Quora Recap: What is a hyperparameter? The model decides! We decide! Learning Methodology Hyperparameters
Learning Methodology Decision tree Hyperparameters Pruning Top-down Bottom-up Maximum depth Minimum samples per leaf Maximum number of terminal nodes
Limiting the number of splits minimizes the problem of overfitting. Two approaches: ● Pre-pruning (top-down) ● Post-pruning (bottom-up) Read more: Notre Dame’s Data Mining class, CSE 40647 Pruning reduces the number of splits in the decision tree. Hyperparameters Pruning
Pre-pruning slows the algorithm before it becomes a fully grown tree. This prevents irrelevant splits. Pre-pruning is a top down approach where the tree is limited in depth before it fully grows. ● E.g. In the malaria diagnosis example, it probably wouldn’t make sense to include questions about a person’s favorite color. ○ It might cause a split, but it likely wouldn’t be a meaningful split. May lead to overfitting Hyperparameters pre-Pruning A useful analogy in nature is a bonsai tree. This is a tree whose growth is slowed starting from when it’s a sapling.
Post-pruning is a bottom up approach where the tree is limited in depth after it fully grows. Grow the full tree, then prune by merging terminal nodes together. 1. Split data into training and validation set 2. Using the decision tree yielded from the training set, merge two terminal nodes together 3. Calculate error of tree with merged nodes and tree without merged nodes 4. If tree with merged nodes has lower error, merge leaf nodes and repeat 2-4. Hyperparameters post-Pruning A useful analogy in nature is pruned bushes. Bushes are grown to their full potential, then are cut and shaped.
Maximum depth defines the maximum number of layers a tree can have. For example, a maximum depth of 4 means a tree can be split between 1 to 4 times. L1 L1 L2 L3 L3 L4 L4 L2 L2 L2 Maximum depth reached, no more splitting Hyperparameters Maximum depth
Go watch Beyonce Are my parents in town? Is it raining? Is there a concert this weekend? NY Is it Maya’s birthday? Dancing!Go for a walkIs it May 5th? Y Y NN Y Go to the museum exhibit that opens on May 12 Y Here we set the hyperparameter max depth to 2 for Sam’s decision tree. Learning Methodology Hyperparameters
Minimum observations per end node This hyperparameter establishes a minimum number of observations in an end node, which reduces the possibility of modelling data noise. Source 5000 2000 3000 1250 850 550 100 750 750 1400 600 Minimum samples per end node = 100 Hyperparameters Minimum observations per lead
Maximum number of terminal nodes limits the number of branches in our tree. The maximum terminal nodes limits the number of branches in our tree. Again, this limits overfitting and reduces the possibility of modelling noise. = terminal nodes Hyperparameters Maximum number of terminal nodes
Minimum impurity ● Recall the Information Gain cost function ● The model iterates until it’s reached a certain level of impurity Hyperparameters Minimum impurity
Which hyperparameter should I use? No objectively best hyperparameter for each model. Use trial and error - see how each changes your results! Learning Methodology Hyperparameters
Bottom-up pruning X X X X Selectively merges some terminal nodes together X X Learning Methodology Optimization Process
Bottom-up pruning The model randomly selects the merge marked in the tree. The model calculates: Error of tree without merge = a Error of tree with merge = b If b < a, it chooses to merge! … And repeat Let’s see how a single merge works: Learning Methodology Optimization Process
Go watch Beyonce Are my parents in town? Is it raining? Is there a concert this weekend? NY Is Beyonce playing? Dancing!Go for a walkIs it May 5th? Y Y NN Go to the museum exhibit that opens on May 12 Y Y Learning Methodology Optimization Process Here we prune Sam’s decision tree bottom-up by merging terminal nodes.
Learning Methodology Learning Methodology What is our loss function? Optimization process How does our ML model learn?
Learning Methodology Supervised Learning What is our loss function? Gini Index, Information gain, RMSE Optimization process Pruning Learning Methodology How does our ML model learn? Iteration! Evaluating different splits, deciding which one’s best
End of the module.
✓ Decision trees ✓ Intuition ✓ The “best” split ✓ Model performance ✓ Model optimization (pruning) Checklist:
Advanced resources
● Textbooks ○ An Introduction to Statistical Learning with Applications in R (James, Witten, Hastie and Tibshirani): Chapter 8 ○ The Elements of Statistical Learning: Data Mining, Inference, and Prediction (Hastie, Tibshirani, Friedman): Chapter 9 ● Online resources ○ Analytics Vidhya’s guide to understanding tree-based methods Want to take this further? Here are some resources we recommend:
You are on fire! Go straight to the next module here. Need to slow down and digest? Take a minute to write us an email about what you thought about the course. All feedback small or large welcome! Email: sara@deltanalytics.org
Congrats! You finished module 5! Find out more about Delta’s machine learning for good mission here.

More Related Content

PPT
Machine learning with Big Data power point presentation
byDavid Raj Kanthi
 
PDF
generative-ai-fundamentals and Large language models
byAdventureWorld5
 
PPTX
KNN Algorithm - How KNN Algorithm Works With Example | Data Science For Begin...
bySimplilearn
 
PDF
How AI is Transforming Project Management - PMI Silver Spring Chapter - Octob...
byHector Del Castillo, CPM, CPMM
 
PPTX
Random forest
byMusa Hawamdah
 
PPTX
Random Forest Classifier in Machine Learning | Palin Analytics
byPalin analytics
 
PPTX
Introduction to Random Forests by Dr. Adele Cutler
bySalford Systems
 
PPTX
Federated Learning: ML with Privacy on the Edge 11.15.18
byCloudera, Inc.
 
Machine learning with Big Data power point presentation
byDavid Raj Kanthi
 
generative-ai-fundamentals and Large language models
byAdventureWorld5
 
KNN Algorithm - How KNN Algorithm Works With Example | Data Science For Begin...
bySimplilearn
 
How AI is Transforming Project Management - PMI Silver Spring Chapter - Octob...
byHector Del Castillo, CPM, CPMM
 
Random forest
byMusa Hawamdah
 
Random Forest Classifier in Machine Learning | Palin Analytics
byPalin analytics
 
Introduction to Random Forests by Dr. Adele Cutler
bySalford Systems
 
Federated Learning: ML with Privacy on the Edge 11.15.18
byCloudera, Inc.
 

What's hot

PPTX
Decision Trees for Classification: A Machine Learning Algorithm
byPalin analytics
 
PDF
Real World End to End machine Learning Pipeline
bySrivatsan Srinivasan
 
PDF
Module 1 introduction to machine learning
bySara Hooker
 
PDF
Data Science - Part VIII - Artifical Neural Network
byDerek Kane
 
PPTX
Machine Learning and Real-World Applications
byMachinePulse
 
PDF
Credit EDA Case Study : Exploratory Data Analysis on Bank Loan Data
byPRABHASH GOKARN
 
PPTX
Pre trained language model
byJiWenKim
 
PDF
Unified Approach to Interpret Machine Learning Model: SHAP + LIME
byDatabricks
 
PDF
Data Science: Applying Random Forest
byEdureka!
 
PDF
Big Data analytics best practices
byThe Marketing Distillery
 
PPTX
Understanding Large Language Models (1).pptx
byRabikaKhalid
 
PPTX
Machine Learning Using Python
bySavitaHanchinal
 
PPTX
Telecom Churn Prediction Presentation
byPinintiHarishReddy
 
PDF
Enterprise Knowledge Graph
byLukas Masuch
 
PDF
Knowledge Graphs and Generative AI
byNeo4j
 
PDF
Exploring Generating AI with Diffusion Models
byKonfHubTechConferenc
 
PDF
prompt engineering
byprads6
 
PDF
Gen AI Cognizant & AWS event presentation_12 Oct.pdf
byPhilipBasford
 
PPTX
Data Analytics
byVala Ali Rohani
 
PPTX
Shap
byGiovanni Bruner
 
Decision Trees for Classification: A Machine Learning Algorithm
byPalin analytics
 
Real World End to End machine Learning Pipeline
bySrivatsan Srinivasan
 
Module 1 introduction to machine learning
bySara Hooker
 
Data Science - Part VIII - Artifical Neural Network
byDerek Kane
 
Machine Learning and Real-World Applications
byMachinePulse
 
Credit EDA Case Study : Exploratory Data Analysis on Bank Loan Data
byPRABHASH GOKARN
 
Pre trained language model
byJiWenKim
 
Unified Approach to Interpret Machine Learning Model: SHAP + LIME
byDatabricks
 
Data Science: Applying Random Forest
byEdureka!
 
Big Data analytics best practices
byThe Marketing Distillery
 
Understanding Large Language Models (1).pptx
byRabikaKhalid
 
Machine Learning Using Python
bySavitaHanchinal
 
Telecom Churn Prediction Presentation
byPinintiHarishReddy
 
Enterprise Knowledge Graph
byLukas Masuch
 
Knowledge Graphs and Generative AI
byNeo4j
 
Exploring Generating AI with Diffusion Models
byKonfHubTechConferenc
 
prompt engineering
byprads6
 
Gen AI Cognizant & AWS event presentation_12 Oct.pdf
byPhilipBasford
 
Data Analytics
byVala Ali Rohani
 
Shap
byGiovanni Bruner
 

Similar to Module 5: Decision Trees

PPTX
Decision Tree Machine Learning Detailed Explanation.
byDrezzingGaming
 
DOCX
Classification Using Decision Trees and RulesChapter 5.docx
bymonicafrancis71118
 
PDF
Understanding Decision Trees in Machine Learning: A Comprehensive Guide
byCyberPro Magazine
 
PPTX
machine learning decision tree algorithm
bymustaq4
 
PDF
13 Machine Learning Supervised Decision Trees
byAndres Mendez-Vazquez
 
PPTX
Yellow_Colorful_Animated_Illustration_Science_Theme_Presentation_(1)[1].pptx
bytyresse278
 
PPTX
Decision Tree Algorithm With Example | Decision Tree In Machine Learning | Da...
bySimplilearn
 
PPTX
Decision trees
bynandini patil
 
PPTX
Ai & Machine learning - 31140523010 - BDS302.pptx
byBhaktMahadevKA
 
PPSX
Classification Using Decision tree
byMohd. Noor Abdul Hamid
 
PDF
Machine Learning - Supervised Learning Techniques- Decision Tree.pdf
byBapusahebDange
 
PPTX
supervised machine learning algorithms support vector machine
bypranalisonawane8600
 
PPTX
ML-Lecture06_07.pptxxxx bjkf mlllllllllll
bymartino7mina
 
PPT
decisiontrees.ppt
byLvlShivaNagendra
 
PPT
decisiontrees.ppt
byPriyadharshiniG41
 
PPT
decisiontrees (3).ppt
byLvlShivaNagendra
 
PDF
Decision Tree-ID3,C4.5,CART,Regression Tree
bySharmila Chidaravalli
 
PDF
Unit 3_Classification_Decision Tree_ASM.pdf
byKanchanPatil34
 
PDF
Machine Learning Unit-5 Decesion Trees & Random Forest.pdf
byAdityaSoraut
 
PDF
PREDICTION OF DISEASE WITH MINING ALGORITHMS IN MACHINE LEARNING
byIRJET Journal
 
Decision Tree Machine Learning Detailed Explanation.
byDrezzingGaming
 
Classification Using Decision Trees and RulesChapter 5.docx
bymonicafrancis71118
 
Understanding Decision Trees in Machine Learning: A Comprehensive Guide
byCyberPro Magazine
 
machine learning decision tree algorithm
bymustaq4
 
13 Machine Learning Supervised Decision Trees
byAndres Mendez-Vazquez
 
Yellow_Colorful_Animated_Illustration_Science_Theme_Presentation_(1)[1].pptx
bytyresse278
 
Decision Tree Algorithm With Example | Decision Tree In Machine Learning | Da...
bySimplilearn
 
Decision trees
bynandini patil
 
Ai & Machine learning - 31140523010 - BDS302.pptx
byBhaktMahadevKA
 
Classification Using Decision tree
byMohd. Noor Abdul Hamid
 
Machine Learning - Supervised Learning Techniques- Decision Tree.pdf
byBapusahebDange
 
supervised machine learning algorithms support vector machine
bypranalisonawane8600
 
ML-Lecture06_07.pptxxxx bjkf mlllllllllll
bymartino7mina
 
decisiontrees.ppt
byLvlShivaNagendra
 
decisiontrees.ppt
byPriyadharshiniG41
 
decisiontrees (3).ppt
byLvlShivaNagendra
 
Decision Tree-ID3,C4.5,CART,Regression Tree
bySharmila Chidaravalli
 
Unit 3_Classification_Decision Tree_ASM.pdf
byKanchanPatil34
 
Machine Learning Unit-5 Decesion Trees & Random Forest.pdf
byAdityaSoraut
 
PREDICTION OF DISEASE WITH MINING ALGORITHMS IN MACHINE LEARNING
byIRJET Journal
 

More from Sara Hooker

PDF
Module 9: Natural Language Processing Part 2
bySara Hooker
 
PDF
Module 8: Natural language processing Pt 1
bySara Hooker
 
PDF
Module 7: Unsupervised Learning
bySara Hooker
 
PDF
Module 6: Ensemble Algorithms
bySara Hooker
 
PDF
Module 4: Model Selection and Evaluation
bySara Hooker
 
PDF
Module 3: Linear Regression
bySara Hooker
 
PDF
Module 2: Machine Learning Deep Dive
bySara Hooker
 
PDF
Module 1.3 data exploratory
bySara Hooker
 
PDF
Module 1.2 data preparation
bySara Hooker
 
PDF
Storytelling with Data (Global Engagement Summit at Northwestern University 2...
bySara Hooker
 
PPTX
Delta Analytics Open Data Science Conference Presentation 2016
bySara Hooker
 
Module 9: Natural Language Processing Part 2
bySara Hooker
 
Module 8: Natural language processing Pt 1
bySara Hooker
 
Module 7: Unsupervised Learning
bySara Hooker
 
Module 6: Ensemble Algorithms
bySara Hooker
 
Module 4: Model Selection and Evaluation
bySara Hooker
 
Module 3: Linear Regression
bySara Hooker
 
Module 2: Machine Learning Deep Dive
bySara Hooker
 
Module 1.3 data exploratory
bySara Hooker
 
Module 1.2 data preparation
bySara Hooker
 
Storytelling with Data (Global Engagement Summit at Northwestern University 2...
bySara Hooker
 
Delta Analytics Open Data Science Conference Presentation 2016
bySara Hooker
 

Recently uploaded

PDF
Configure and Manage Systemd Timers- RHCSA (RH134).pdf
byLinuxCert Guru
 
PDF
Getting Started with Apache Spark: Big Data Made Simple [Free Meetup]
byHaim Michael
 
PDF
The Enterprise Web3 Landscape - a view from Kaleido based on the past 10 year...
byPeter Broadhurst
 
PPTX
Retrieval Augmented Generation- The Synergistic Power of Prompt Engineering
bySemantic SEO BD
 
PDF
2026_01_28 - OpenMetadata Community Meeting.pdf
byOpenMetadata
 
PPTX
NTG - Data Center Management System Software
byMustafa Kuğu
 
PDF
Parental Control App for Phones_ The Complete 2026 Guide for Safer, Smarter P...
byRyan Cooper
 
PPTX
Introduction to Artificial Intelligence (AI).pptx
byammar414783
 
PDF
Adapt.com Seed Fundraising Deck | The AI Computer for Business
byashley459565
 
PDF
Agentic-Document-Extraction-2026-Presentation.pdf
byTamanna
 
PDF
Bettersize | BeSEC Series Product Brochure
byBettersize Instruments
 
PDF
What Is the Azure AI Foundry and Why Does It Matter for Enterprises?
byjohncarterjn
 
PDF
Why Many Smart Device Platforms Fail to Scale?
byPromeraki Developments
 
PDF
Computer-Based Training (CBT) The Backbone of Modern Technical & Defence Trai...
bycomputerbasedtrainin1
 
PPTX
Cyber security chapter 1 for learning and educating to the students who want ...
byGulMohammadi
 
PDF
Chapter 4 Network Security in computer security
byGetnet Tigabie Askale -(GM)
 
PDF
How to build hackthon projects from ZERO!
byishantyadav1111
 
PDF
Post-Hackathon-Learnings-Maximizing-Impact-Beyond-the-Event.pdf
byishantyadav1111
 
PDF
January 2026 OpenMetadata Community Spotlight - OpenMetadata @ Wix.pdf
byOpenMetadata
 
PDF
AI and Zero Trust: What it takes to do it right
byMark Simos
 
Configure and Manage Systemd Timers- RHCSA (RH134).pdf
byLinuxCert Guru
 
Getting Started with Apache Spark: Big Data Made Simple [Free Meetup]
byHaim Michael
 
The Enterprise Web3 Landscape - a view from Kaleido based on the past 10 year...
byPeter Broadhurst
 
Retrieval Augmented Generation- The Synergistic Power of Prompt Engineering
bySemantic SEO BD
 
2026_01_28 - OpenMetadata Community Meeting.pdf
byOpenMetadata
 
NTG - Data Center Management System Software
byMustafa Kuğu
 
Parental Control App for Phones_ The Complete 2026 Guide for Safer, Smarter P...
byRyan Cooper
 
Introduction to Artificial Intelligence (AI).pptx
byammar414783
 
Adapt.com Seed Fundraising Deck | The AI Computer for Business
byashley459565
 
Agentic-Document-Extraction-2026-Presentation.pdf
byTamanna
 
Bettersize | BeSEC Series Product Brochure
byBettersize Instruments
 
What Is the Azure AI Foundry and Why Does It Matter for Enterprises?
byjohncarterjn
 
Why Many Smart Device Platforms Fail to Scale?
byPromeraki Developments
 
Computer-Based Training (CBT) The Backbone of Modern Technical & Defence Trai...
bycomputerbasedtrainin1
 
Cyber security chapter 1 for learning and educating to the students who want ...
byGulMohammadi
 
Chapter 4 Network Security in computer security
byGetnet Tigabie Askale -(GM)
 
How to build hackthon projects from ZERO!
byishantyadav1111
 
Post-Hackathon-Learnings-Maximizing-Impact-Beyond-the-Event.pdf
byishantyadav1111
 
January 2026 OpenMetadata Community Spotlight - OpenMetadata @ Wix.pdf
byOpenMetadata
 
AI and Zero Trust: What it takes to do it right
byMark Simos
 

Module 5: Decision Trees

  • 1.
  • 2.
    This course contentis being actively developed by Delta Analytics, a 501(c)3 Bay Area nonprofit that aims to empower communities to leverage their data for good. Please reach out with any questions or feedback to inquiry@deltanalytics.org. Find out more about our mission here. Delta Analytics builds technical capacity around the world.
  • 3.
  • 4.
    ❏ Decision trees ❏Intuition ❏ The “best” split ❏ Model performance ❏ Model optimization (pruning) Module Checklist:
  • 5.
    Where are we? We’velaid much of the groundwork for machine learning, and introduced our very first algorithm of linear regression. Now, we can focus on expanding our algorithm toolkit. Decision trees are another type of algorithm that can accomplish the same objective of prediction that linear regression can. We will also go deeper into the pros and cons of decision trees in this module.
  • 6.
    Where are we? Supervised Algorithms Let’sdo a quick intro to decision trees and ensembles! Linear regression Decision tree Ensemble Algorithms
  • 7.
    Decision Tree Today, we willstart by looking at a decision tree algorithm. A decision tree is a set of rules we can use to classify data into categories (also can be used for regression tasks). Humans often use a similar approach to arrive at a conclusion. For example, doctors ask a series of questions to diagnose a disease. A doctor’s goal is to ask the minimum number of questions needed to arrive at the correct diagnosis. What is wrong with my patient? Help me put together some questions I can use to diagnose patients correctly.
  • 8.
    Decision Tree Decision trees areintuitive because they are similar to how we make many decisions. My mental diagnosis decision tree might look something like this. How is the way I think about this different from a machine learning algorithm? Does the patient have a temperature over 37C? Vomiting? Diarrhea? NY Malaria FluFluIs malaria present in the region? Y Y NN FluMalaria N Y
  • 9.
    Decision Tree Decision trees areintuitive and can handle more complex relationships than linear regression can. A linear regression is a single global trend line. This makes it inflexible for more sophisticated relationships. Sources: https://www.slideshare.net/ANITALOKITA/winnow-vs-perceptron, http://www.turingfinance.com/regression-analysis-using-python-sta tsmodels-and-quandl/
  • 10.
    We will useour now familiar framework to discuss both decision trees and ensemble algorithms: Task What is the problem we want our model to solve? Performance Measure Quantitative measure we use to evaluate the model’s performance. Learning Methodology ML algorithms can be supervised or unsupervised. This determines the learning methodology. Source: Deep Learning Book - Chapter 5: Introduction to Machine Learning
  • 11.
    Task What is theproblem we want our model to solve? Defining f(x) What is f(x) for a decision tree and random forest? Feature engineering & selection What is x? How do we decide what explanatory features to include in our model? What assumptions does a decision tree make about the data? Do we have to transform the data? Is our f(x) correct for this problem?
  • 12.
    Learning Methodology Decision tree modelsare supervised. How does that affect the learning processing? What is our loss function? Every supervised model has a loss function it wants to minimize. Optimization process How does the model minimize the loss function? How does our ML model learn? Overview of how the model teaches itself.
  • 13.
    Performance Quantitative measure weuse to evaluate the model’s performance. Measures of performance Metrics we use to evaluate our model Feature Performance Determination of feature importance Overfitting, underfitting, bias, variance Ability to generalize to unseen data
  • 14.
  • 15.
    Decision tree: modelcheat sheet ● Susceptible to overfitting (poor performance on test set) ● High variance between data sets ● Can become unstable: small variations in the training data result in completely different trees being generated ● Mimics human intuition closely (we make decisions in the same way!) ● Not prescriptive (i.e., decision trees do not assume a normal distribution) ● Can be intuitively understood and interpreted as a flow chart, or a division of feature space. ● Can handle nonlinear data (no need to transform data) Pros Cons
  • 16.
  • 17.
    Task How does adoctor diagnose her patients based on their symptoms? What are we predicting?
  • 18.
    Task A doctorbuilds a diagnosis from your symptoms. I start by asking patients a series of questions about their symptoms. I use that information to build a diagnosis. Flu Malaria Flu Flu diagnosis Yes No No Yes Severe Severe Mild None Shaking chills vomitingtemp X1 X2 X3 Y Y* 39.5°C 37.8°C 37.2°C 37.2°C predicted diagnosis Flu Malaria Malaria Flu There are some questions the doctor does not need to ask because she learns it from her environment. (For example, a doctor would know if malaria present in this region.) A machine, however, would have to be explicitly taught this feature.
  • 19.
    Task A doctor makesa mental diagnosis path to arrive at her conclusion. She is building a decision tree! How does the way I think about how to decide the value of the split compare to a machine learning algorithm? Does the patient have a temperature over 37C? vomiting Severe shaking chills NY malaria flufluIs malaria present in the region Y Y NN flumalaria N Y
  • 20.
    At each split,we can determine the best question to maximize the number of observations correctly grouped under the right category. ● Both a doctor and decision tree try to arrive at the minimum number of questions (splits) that needs to be asked to correctly diagnose the patient. ● Key difference: how the order of the questions and the split value are determined. A doctor will do this based upon experience, a decision tree will formalize this concept using a loss function. Based upon my experience as a doctor, I know there are certain questions whose answers quickly separate flu from malaria. Human Intuition Decision Tree
  • 21.
    To determine whethera new patient has malaria, a doctor uses her experience and education, and machine learning creates a model using data. By using a machine learning model, our doctor is able to use both her experience and data to make the best decision! Machine learning adds the power of data to our doctor’s task. Task
  • 22.
    Mr. Model createsa flow chart (the model) by separating our entire dataset into distinct categories. Once we have this model, we’ll know what category our new patient falls into! Decision trees act in the same manner as human categorization, they (split) the data based upon answers to questions. Where do I go? Malaria MalariaNo malaria Task
  • 23.
    To get asense of how this “splitting” works, let’s play a guessing game. I am thinking of something that is blue. You may ask 10 questions to guess what it is.
  • 24.
    The first fewquestions you would probably ask may include: - Is it alive? (No) - Is it in nature? (Yes)
  • 25.
    Then, as yougot closer to the answer, your questions would become more specific. - Is it solid or liquid? (Liquid) - Is it the ocean? (Yes!)
  • 26.
    Some winning strategiesinclude: ● Use questions early on that eliminate the most possibilities. ● Questions often start broad and become more granular. This process is your mental decision tree. In fact, this strategy captures many of the qualities of our algorithm!
  • 27.
    You created yourown decision tree based on your own experience of what you know is blue to make an educated guess as to what I was thinking of (the ocean). Similarly, a decision tree model will make an educated guess, but instead of using experience, it uses data. Now, let’s build a formal vocabulary for discussing decision trees.
  • 28.
    Like a linearregression, a decision tree has explanatory features and an outcome. Our f(x) is the decision path from the top of the tree to the final outcome. feature feature outcome outcome model model Decision Tree Defining f(x)
  • 29.
    feature outcome model Decision Tree New vocabulary Internal node Terminal node Split Split The“decisions” of the decision tree model. The model decides which features to use to split the data. Root node Our starting point. The first split occurs here along the feature that the model decides is most important. Internal node Intermediate splits. Corresponds to a subset of the entire dataset. Terminal node Predicted outcome. Corresponds to a smaller subset of the entire dataset. Root node
  • 30.
    Decision Tree New vocabulary Splits Root node Feature 2 Feature1 Feature3 Thisvisualization of splits in feature space is a different but equally accurate way to conceptualize decision trees as the flow chart in the previous slide. A decision tree splits the feature space (the dataset) along features. The order of splits are determined by the algorithm.
  • 31.
    Task Splits at thetop of the tree have an outsized importance on final outcome. What is the root node, split, internal node and terminal node in this example? Does the patient have a temperature over 37C? vomiting Severe shaking chills NY malaria flufluIs malaria present in the region Y Y NN flumalaria N Y Some additional terminology Internal node Terminal node Split Root node
  • 32.
    Decision Tree Let’s look atanother question to combine our intuition with formal vocabulary. What should Sam do this weekend? Let’s get this weekend started! Dancing Cooking dinner at home Eating at fancy restaurant Music concert Walk in the park Y = Choice of weekend activity Training data set: You have a dataset of what she has done every weekend for the last two years. Defining f(x)
  • 33.
    Decision Tree Task What willSam do this weekend? Dancing Cooking dinner at home Eating out Music concert Walk in the park Walk in the park Dancing Eating out Y What will Sam do? $80No Savings ($) X2 Parents in town Has a partner Yes X3X1 We have historical data on what Sam has done on past weekends (Y), as well some explanatory variables.
  • 34.
    In this example,we predict Sam’s weekend activity using decision rules trained on historical weekend behavior. How much $$ do I have? Raining? Partner? >=$50<$50 Concert! Dancing!Walk in the park!Movie! Y Y NN Decision Tree Task Defining f(x) The decision tree f(x) predicts the value of a target variable by learning simple decision rules inferred from the data features. Our most important predictive feature is Sam’s budget. How do we know this? Because it is the root node.
  • 35.
    A decision treesplits the dataset (“feature space”). Here, the entire dataset = data from 104 weekends. You can see how each split subsets the data into progressively smaller groups. Now, when we want to predict what will happen this weekend, we can! How much $$ do I have? Raining? Partner? < $50 Concert! Dancing!Walk in the park!Movie! Y Y NN Decision Tree Task f(x) as a spatial function >= $50 n=104 n=17 n=30 n=74 n=6n=13 An example of how the algorithm works: n=68
  • 36.
    How much $$do I have? Raining? Partner? < $50 Concert! Dancing!Walk in the park!Movie! Y Y NN Decision Tree Task f(x) as a spatial function >= $50 n=104 n=17 n=30 n=74 n=6n=13 Each of the four weekend options are grouped spatially by our splits. n=68 Visualized in the data: How much $$ do I have? Raining? Girlfriend?
  • 37.
    Now we understandthe mechanics of the decision tree task. But how does a decision tree learn? How does it know where to split the data, and in what order? We turn now to examine decision trees’ learning methodology.
  • 38.
  • 39.
    At each split,we can determine the best question to ask to maximize the number of observations correctly grouped under the right category. Based upon my experience as a doctor, I know there are certain questions whose answers quickly separate flu from malaria. Remember that the key difference between a doctor and our model is how the order of the questions and the split value are determined. Human Intuition Decision Tree Learning Methodology How does our f(x) learn?
  • 40.
    key difference betweena doctor and our model is how the order of the questions and the split value are determined. Learning Methodology How does our f(x) learn? The two key levers that can be changed to improve accuracy of our medical diagnosis are: - The order of the questions - The split value at each node. (For example the temperature boundary) A doctor will make these decisions based upon experience, a decision tree will set these parameters to minimize our loss function by learning from the data.
  • 41.
    Recap: Loss function Linear Regression Aloss function quantifies how unhappy you would be if you used f(x) to predict Y* when the correct output is y. It is the object we want to minimize. Remember: All supervised models have a loss function (sometimes also known as the cost function) they must optimize by changing the model parameters to minimize this function. Sound familiar? We just went over a similar optimization process for linear regression (our loss function there was MSE). Source: Stanford ML Lecture 1
  • 42.
    Values that controlthe behavior of the model. The model learns what parameters are from data. Parameters How does our decision tree learn? Parameters of a model are values that our model controls to minimize our loss function. Our model sets these parameters by learning from the data. Learning Methodology One of the parameters our model controls are the split values. For example, our model learns that $50 is the best split to predict whether Sam eats out or stays at home. How much $$ do I have? Cook at home Eat at restaurants < $50 >= $50
  • 43.
    How does our decision treelearn? We have two decision tree parameters: split decision rule (value of b) and the ordering of features Learning Methodology >=b How much $$ do I have? Cook at home <b Partner? Concert! Dancing! b=0 b=1 Our model controls the split decision rule and the ordering of the features. Our model learns what best fits the data by moving the split value up or down and by trying many combinations of decision rule ordering.
  • 44.
    Central problem: Howdo we learn the “best” split?
  • 45.
    How does our decision treelearn? There are so many possible decision paths and split values - in fact, an infinite amount! How does our model choose? Learning Methodology >=b How much $$ do I have? Cook at home <b Partner? Concert! Dancing! b=0 b=1 Our model checks the parameter choices against the loss function every time it makes a change. It checks whether the error went up, down or stayed the same. If it went down, our model knows it did something right! Oh no! That made it worse. Let’s try something else.
  • 46.
    Our random initializationof parameters give us a unsurprisingly high initial error How does our decision tree learn? Imagine that is a game. We start with a random ordering of features and set b to completes random values. Learning Methodology Our model’s job is to change the parameters so that every time he updates the loss goes down. The game is over when our model is able to reduce the error to e, the irreducible error.
  • 47.
    Regression Classification Continuous variable Categorical variable Aclassification problem is when are trying to predict whether something belongs to a category, such as “red” or “blue” or “disease” and “no disease”. A regression problem is when we are trying to predict a numerical value given some input, such as “dollars” or “weight”. Source: Andrew Ng , Stanford CS229 Machine Learning Course Decision trees also can be used for two types of tasks! Recap of tasks:
  • 48.
    What is our lossfunction? Our decision tree loss function depends on the type of task. Learning Methodology I can minimize all types of loss functions! The most common loss functions for decision trees include: For classification trees: 1. Gini Impurity 2. Entropy For regression trees: 3. Mean Squared Error For example, the loss function for a regression decision tree should feel familiar. It is the same loss function we used for linear regression!
  • 49.
    Information gain attemptsto minimize entropy in each subnode. Entropy is defined as a degree of disorganization. If the sample is completely homogeneous, then the entropy is zero. If the sample is an equally divided (50% – 50%), it has entropy of one. Learning Methodology For classification trees, we can use information gain! How would you rank the entropy of these circles? Source
  • 50.
    All things thatare the same need to be put away in the same terminal node. Learning Methodology Information Theory is a neat freak and values organization. How would you rank the circles in terms of entropy? Low EntropyHigh Entropy Medium Entropy Our low entropy population is entirely homogenous: the entropy is 0!
  • 51.
    The Information Gainalgorithm: 1. Calculates entropy of parent node 2. Calculates entropy of each individual node of split, and calculates weighted average of all sub-nodes available in split. The algorithm then chooses the split that has the lowest entropy. What is our loss function? Learning Methodology So, how does it work in our decision tree model? I’m going to randomly generate three splits… >$50? Yes No Girlfriend? Yes No Raining? Yes No Split entropy
  • 52.
    This may lookfamiliar - look back at our discussion of linear regression! Decision trees also use MSE. The split with lower MSE is selected as the criteria to split the population. What is our loss function? Learning Methodology Regression trees use Mean Squared Error. Y-Y* For every point in our dataset, measure the difference between true Y and predicted Y. ^2 Square each Y-Y* to get the absolute distance, so positive values don’t cancel out negative ones when we sum. Sum Sum across all observations so we get the total error. mean Divide the sum by the number of observations we have.
  • 53.
    The RMSE algorithmproceeds by: 1. Calculating variance for each node. 2. Calculating variance for each split as weighted average of each node variance. The algorithm then selects the split that has the lowest variance. What is our loss function? Learning Methodology Regression trees use Mean Squared Error. I’m going to randomly generate three splits… Amount of $ Yes No # of girlfriends Yes No Likelihood of rain Yes No Split RMSE 3.83 7.28 10.3
  • 54.
  • 55.
    Decision trees provideus with understanding of what features are most important for predicting Y* Recall our intuition: Important splits happen closer to the root node. The intuition is provided by the understanding that the most important splits are at the first nodes. The decision tree tells us what the important splits are (which features cause splits that reduce cost function the most). Performance Feature Performance
  • 56.
    In Sam’s case,our algorithm determined that Sam’s budget was the most important feature in predicting her weekend plans. This makes a lot of sense! $$ saved? Is it raining? Do I have a partner? NY Concert! Dancing!Walk in the park!Movie! Y Y NN Performance Feature Performance Recall our intuition: Important splits happen earlier
  • 57.
    Go watch Beyonce Imagineif the Sam’s decision tree, based on 2 years of weekend data, deteriorated into extremely specific weekend events that occurred in the data. This is overfitting! Are my parents in town? Is it raining? Is there a concert this weekend? NY Is it Maya’s birthday? Dancing!Go for a walkIs it May 5th? Y Y NN Go to the museum exhibit that opens on May 5 Y Y Performance Overfitting
  • 58.
    Performance Ability to generalize to unseendata Our goal in evaluating performance is to find a sweet spot between overfitting and underfitting. If our train data set overfits, it will not generalize to our test set (unseen data) well. However, if it underfits, we are not capturing the complexity of the relationship and our loss will be high! Underfit Overfit Sweet spot Remember that the most important goal we have is to build a model that will generalize well to unseen data.
  • 59.
    Each time weadd a node, we fit additional models to subsets of the data . This means we start to get to know our train data really well but it will impair our ability to generalize to our test data. Overfitting: If each terminal node is an individual observation, it is overfit. Performance Ability to generalize to unseen data Let’s take a look at a concrete example of optimizing our model! Unfortunately, decision trees are very prone to overfitting. We have to be very careful in evaluating this.
  • 60.
  • 61.
    Go watch Beyonce Nowthat we understand how overfitting is bad we can use a few different approaches to avoid it: ● Pruning ● Maximum Depth ● Minimum obs per terminal node Are my parents in town? Is it raining? Is there a concert this weekend? NY Is it Maya’s birthday? Dancing!Go for a walkIs it May 5th? Y Y NN Go to the museum exhibit that opens on May 5 Y Y Learning Methodology Optimization process
  • 62.
    Pruning, max depthand n_ obs in a terminal node are all examples of hyperparameters. Learning Methodology Pruning, max depth and n_ obs in a terminal node are all decision tree hyperparameters set before training. Their values are not learned from the data so the model cannot say anything about them. Hyperparameters are higher level settings of a model that are fixed before training begins. You, not the model decide what the hyperparameters are!
  • 63.
    ● In linearregression, the coefficients were parameters. Y = a + b1 x1 + b2 x2 + … + e ○ Parameters are learned from the training data using the chosen algorithm. ● Hyperparameters cannot be learned from the training process. They express “higher-level” properties of the model such as its complexity or how fast it should learn. Source: Quora Recap: What is a hyperparameter? The model decides! We decide! Learning Methodology Hyperparameters
  • 64.
    Learning Methodology Decision tree Hyperparameters Pruning Top-down Bottom-up Maximumdepth Minimum samples per leaf Maximum number of terminal nodes
  • 65.
    Limiting the numberof splits minimizes the problem of overfitting. Two approaches: ● Pre-pruning (top-down) ● Post-pruning (bottom-up) Read more: Notre Dame’s Data Mining class, CSE 40647 Pruning reduces the number of splits in the decision tree. Hyperparameters Pruning
  • 66.
    Pre-pruning slows thealgorithm before it becomes a fully grown tree. This prevents irrelevant splits. Pre-pruning is a top down approach where the tree is limited in depth before it fully grows. ● E.g. In the malaria diagnosis example, it probably wouldn’t make sense to include questions about a person’s favorite color. ○ It might cause a split, but it likely wouldn’t be a meaningful split. May lead to overfitting Hyperparameters pre-Pruning A useful analogy in nature is a bonsai tree. This is a tree whose growth is slowed starting from when it’s a sapling.
  • 67.
    Post-pruning is abottom up approach where the tree is limited in depth after it fully grows. Grow the full tree, then prune by merging terminal nodes together. 1. Split data into training and validation set 2. Using the decision tree yielded from the training set, merge two terminal nodes together 3. Calculate error of tree with merged nodes and tree without merged nodes 4. If tree with merged nodes has lower error, merge leaf nodes and repeat 2-4. Hyperparameters post-Pruning A useful analogy in nature is pruned bushes. Bushes are grown to their full potential, then are cut and shaped.
  • 68.
    Maximum depth definesthe maximum number of layers a tree can have. For example, a maximum depth of 4 means a tree can be split between 1 to 4 times. L1 L1 L2 L3 L3 L4 L4 L2 L2 L2 Maximum depth reached, no more splitting Hyperparameters Maximum depth
  • 69.
    Go watch Beyonce Aremy parents in town? Is it raining? Is there a concert this weekend? NY Is it Maya’s birthday? Dancing!Go for a walkIs it May 5th? Y Y NN Y Go to the museum exhibit that opens on May 12 Y Here we set the hyperparameter max depth to 2 for Sam’s decision tree. Learning Methodology Hyperparameters
  • 70.
    Minimum observations per endnode This hyperparameter establishes a minimum number of observations in an end node, which reduces the possibility of modelling data noise. Source 5000 2000 3000 1250 850 550 100 750 750 1400 600 Minimum samples per end node = 100 Hyperparameters Minimum observations per lead
  • 71.
    Maximum number ofterminal nodes limits the number of branches in our tree. The maximum terminal nodes limits the number of branches in our tree. Again, this limits overfitting and reduces the possibility of modelling noise. = terminal nodes Hyperparameters Maximum number of terminal nodes
  • 72.
    Minimum impurity ● Recallthe Information Gain cost function ● The model iterates until it’s reached a certain level of impurity Hyperparameters Minimum impurity
  • 73.
    Which hyperparameter shouldI use? No objectively best hyperparameter for each model. Use trial and error - see how each changes your results! Learning Methodology Hyperparameters
  • 74.
    Bottom-up pruning X X X X Selectively mergessome terminal nodes together X X Learning Methodology Optimization Process
  • 75.
    Bottom-up pruning The modelrandomly selects the merge marked in the tree. The model calculates: Error of tree without merge = a Error of tree with merge = b If b < a, it chooses to merge! … And repeat Let’s see how a single merge works: Learning Methodology Optimization Process
  • 76.
    Go watch Beyonce Aremy parents in town? Is it raining? Is there a concert this weekend? NY Is Beyonce playing? Dancing!Go for a walkIs it May 5th? Y Y NN Go to the museum exhibit that opens on May 12 Y Y Learning Methodology Optimization Process Here we prune Sam’s decision tree bottom-up by merging terminal nodes.
  • 77.
    Learning Methodology Learning Methodology What isour loss function? Optimization process How does our ML model learn?
  • 78.
    Learning Methodology Supervised Learning What isour loss function? Gini Index, Information gain, RMSE Optimization process Pruning Learning Methodology How does our ML model learn? Iteration! Evaluating different splits, deciding which one’s best
  • 79.
    End of themodule.
  • 80.
    ✓ Decision trees ✓Intuition ✓ The “best” split ✓ Model performance ✓ Model optimization (pruning) Checklist:
  • 81.
  • 82.
    ● Textbooks ○ AnIntroduction to Statistical Learning with Applications in R (James, Witten, Hastie and Tibshirani): Chapter 8 ○ The Elements of Statistical Learning: Data Mining, Inference, and Prediction (Hastie, Tibshirani, Friedman): Chapter 9 ● Online resources ○ Analytics Vidhya’s guide to understanding tree-based methods Want to take this further? Here are some resources we recommend:
  • 83.
    You are onfire! Go straight to the next module here. Need to slow down and digest? Take a minute to write us an email about what you thought about the course. All feedback small or large welcome! Email: sara@deltanalytics.org
  • 84.
    Congrats! You finished module5! Find out more about Delta’s machine learning for good mission here.