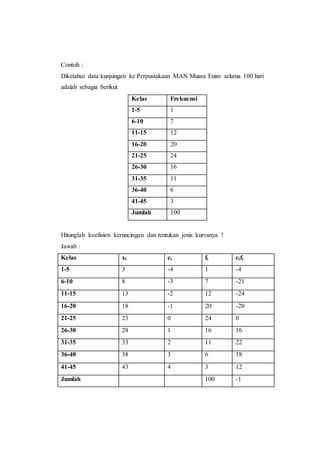
Dokumen tersebut membahas tentang ukuran keruncingan dan jenis-jenis kurva distribusi frekuensi. Terdapat tiga jenis kurva yaitu leptokurtik, mesokurtik, dan platikurtik yang dapat diidentifikasi melalui koefisien kurtosis yang dihitung berdasarkan rumus tertentu. Contoh soal menunjukkan cara menghitung koefisien kurtosis untuk menentukan jenis kurva suatu data.

1. UKURAN KERUNCINGAN
Disusun Oleh :
1. Fatria Anggita (06081181520005)
2. Lorent Agustina Arissanti (06081181520004)
3. Putri Maya Sari (06081181520026)
4. Robiatul Bangka Wiyah (06081281520069)
Program Studi Pendidikan Matematika
Fakultas Keguruan dan Ilmu Pendidikan
Universitas Sriwijaya
2016

2. UKURAN KEMIRINGAN
A. PENGERTIAN UKURAN KEMIRINGAN
Ukuran kemiringan adalah ukuran yang menyatakan sebuah model
distribusi yang mempunyai kemiringan tertentu (Putri, 2012). Apabila
diketahui besarnya nilai ukuran ini maka dapat diketahui pula bagaimana
model distribusinya, apakah distribusi itu simetrik, positif, atau negatif.
B. BENTUK-BENTUK KURVA KEMIRINGAN
Jika kita melihat sebuah kurva frekuensi, kita dapat melihat letak
kecenderungan berkumpulnya nilai-nilai data dengan jelas.
Jika nilai-nilai data tersebar secara merata sebelah kiri maupun di
sebelah kanan rata-rata,kurvanya akan berbentuk simetris.
Jika nilai-nilai data tidak tersebar merata antara sisi-sisi kiri dan
kanan rata-ratanya, kurva akan condong ke kiri atau ke kanan.

3. Untuk mengetahui apakah data mengikuti kurva simetris, kurva
negatif atau kurva positif, kita dapat melihatnya berdasarkan nilai
koefisien kemiringannya, yaitu dengan cara berikut ini.
a. Koefisien kemiringan pertama dari Karl Person
Keterangan:
SK = Koefisien Kemiringan
Mo = Modus
S = Simpangan Standar
𝑋̅ = Rata-rata
b. Koefisien kemiringan kedua dari Karl Person
Keterangan: SK = Koefisien Kemiringan
Mo = Modus
S = Simpangan Standar
𝑋̅ = Rata-rata
c. Koefisien kemiringan menggunakan nilai kuartil
Koefisien kemiringannya =
dimana : K1 = kuartil ke satu, K2 = kuartil ke dua, K3 = kuartil ke tiga
Contoh 1:
Dari suatu sebaran data diketahui nilai rata-ratanya 𝑋̅ = 45,2 , Mo =
43,7 dan S = 19,59. Tentukan koefisien kemiringannya!
Jawab :
𝑆𝐾 =
𝑋̅ − 𝑀 𝑜
𝑆
𝑆𝐾 =
𝑋̅ − 𝑀𝑒
𝑆
𝐾3 − 2𝐾2 + 𝐾1
𝐾3 𝐾1

4. 𝑆𝐾 =
𝑋̅ − 𝑀 𝑜
𝑆
=
45,2− 43,7
19,59
= 0,08
Hasil SK = 0,08 (positif) berarti sebaran datanya miring ke kanan, seperti tampak
pada gambar di bawah.
Contoh 2 :
Tentukan koefisien kemiringan dari data berikut ini !
Nilai f
31-40 1
41-50 2
51-60 5
61-70 15
71-80 25
81-90 20
91-100 12
Jumlah 80
Jawab :
Nilai f xi fixi xi - 𝑥̅ (xi - 𝑥̅)2 fi(xi - 𝑥̅)2
31-40 1 35,5 35,5 -41,1 1682,219 16881,21
41-50 2 45,5 91,0 -31,1 967,21 1934,42
51-60 5 55,5 275,5 -21,1 445,21 2226,05
61-70 15 65,5 982,5 -10,1 102,01 1530,15
71-80 25 75,5 1887,5 -1,1 1,21 30,25
81-90 20 85,5 1710,0 -8,9 79,21 1584,20
91-100 12 95,5 1146,0 -10,9 357,21 4502,52
80 6128 13489,80

5. 𝑥̅ =
∑ 𝑓𝑖 −𝑥 𝑖
∑ 𝑓𝑖
=
6128
80
= 76,6
𝑆2
=
1
𝑛
∑ 𝑓𝑖( 𝑓𝑖 − 𝑥̅)2
𝑆2
=
13489,80
80
= 168,6
𝑆 = 12,98
Median 𝑀𝑒 = 𝑏 + 𝑝(
1
2
𝑛−𝐹
𝑓
)
= 70,5+10(
1
2
80−23
25
)
= 70,5 + 10(
17
25
)
= 70,5 + 6,8 = 77,3
Jadi, SK =
3( 𝑥̅− 𝑀 𝑒)
𝑆
SK =
3(76,6−77,3)
12,98
= −0,16
Karena koefisien kemiringannya negatif dan mendekati nol, model kurvanya
sedikit ke kiri, seperti pada gambar di bawah :

7. UKURAN KERUNCINGAN
A. PENGERTIAN UKURAN KERUNCINGAN
Ukuran kerucingan adalah kepuncakan dari suatu distribusi,
biasanya diambil relatif terhadap distribusi normal (Putri, 2012)
B. DERAJAT KERUNCINGAN DISTRIBUSIFREKUENSI
Dilihat dari segi keruncingannya, kurva distribusi frekuensi dapat
digolongkan menjadi tiga golongan, yaitu :
1. Kurva Leptokurtik
Kurva leptokurtik adalah kurva distribusi yang sangat runcing dan
nilai-nilai datanya sangat terpusat di sekitar nilai rata-rata (Subana,
2000). Perhatikan gambar di bawah :
Gambar Kurva Leptokurtik
2. Kurva Mesokurtik
Kurva mesokurtik adalah kurva yang kemiringannya sedang dan
merupakan penggambaran dari suatu distribusi normal (Subana;102).
Perhatikan gambar di bawah :

8. Gambar Kurva Mesokurtik
3. Kurva Platikurtik
Kurva platikurtik adalah kurva yang betuknya mendatar dan nilai-
nilai datanya tersebar secara merata sampai jauh dari rata-ratanya
(Subana;103). Perhatikan gambar di bawah :
Gambar Kurva Platikurtik
Untuk mengetahui apakah suatu kurva distribusi merupakan leptokurtik,
mesokurtik, atau platikurtik, kita dapat menggunakan suatu ukuran keruncingan
atau koefisien kurtosis. Untuk menghitung tingkat keruncingan suatu kurva
dipergunakan rumus 𝛼4 yang di rumuskan berikut ini :

9. 1. Data Tidak Berkelompok
𝛼4 =
𝑚4
𝑆4
=
1
𝑛
∑
(𝑥 𝑖 − 𝑥̅)4
𝑆4
𝑛
𝑖=1
Keterangan :
𝛼4 = 𝑘𝑜𝑒𝑓𝑖𝑠𝑖𝑒𝑛 𝑘𝑢𝑟𝑡𝑜𝑠𝑖𝑠
𝑥 𝑖 = 𝑛𝑖𝑙𝑎𝑖 𝑑𝑎𝑡𝑎 𝑘𝑒 𝑖
𝑥̅ = 𝑁𝑖𝑙𝑎𝑖 𝑟𝑎𝑡𝑎 − 𝑟𝑎𝑡𝑎
𝑛 = 𝑏𝑎𝑛𝑦𝑎𝑘𝑛𝑦𝑎 𝑑𝑎𝑡𝑎
𝑆 = 𝑠𝑖𝑚𝑝𝑎𝑛𝑔𝑎𝑛 𝑠𝑡𝑎𝑛𝑑𝑎𝑟
2. Data Kelompok
𝛼4 =
𝑚4
𝑆4
=
1
𝑛
∑ (𝑓𝑖( 𝑥𝑖 − 𝑥̅)4
)𝑛
𝑖=1
𝑆4
Keterangan :
𝛼4 = 𝑘𝑜𝑒𝑓𝑖𝑠𝑖𝑒𝑛 𝑘𝑢𝑟𝑡𝑜𝑠𝑖𝑠
𝑥 𝑖 = 𝑛𝑖𝑙𝑎𝑖 𝑑𝑎𝑡𝑎 𝑘𝑒 𝑖
𝑥̅ = 𝑁𝑖𝑙𝑎𝑖 𝑟𝑎𝑡𝑎 − 𝑟𝑎𝑡𝑎
𝑓𝑖 = 𝑓𝑟𝑒𝑘𝑢𝑒𝑛𝑠𝑖 𝑘𝑒𝑙𝑎𝑠 𝑘𝑒 − 𝑖
𝑛 = 𝑏𝑎𝑛𝑦𝑎𝑘𝑛𝑦𝑎 𝑑𝑎𝑡𝑎
𝑆 = 𝑠𝑖𝑚𝑝𝑎𝑛𝑔𝑎𝑛 𝑠𝑡𝑎𝑛𝑑𝑎𝑟
Berdasarkan koefisien kurtosisnya, jenis kurvanya dikategorikan sebagai
berikut :
1. Jika 𝛼4 > 3, kurvanya runcing (liptokurtik)
2. Jika 𝛼4 = 3, kurvanya distribusi normal (mesokurtik)
3. Jika 𝛼4 < 3, kurvanya agak datar (platikurtik)

10. Contoh :
Diketahui data kunjungan ke Perpustakaan MAN Muara Enim selama 100 hari
adalah sebagia berikut
Kelas Frekuensi
1-5 1
6-10 7
11-15 12
16-20 20
21-25 24
26-30 16
31-35 11
36-40 6
41-45 3
Jumlah 100
Hitunglah koefisien keruncingan dan tentukan jenis kurvanya !
Jawab :
Kelas xi ci fi cifi
1-5 3 -4 1 -4
6-10 8 -3 7 -21
11-15 13 -2 12 -24
16-20 18 -1 20 -20
21-25 23 0 24 0
26-30 28 1 16 16
31-35 33 2 11 22
36-40 38 3 6 18
41-45 43 4 3 12
Jumlah 100 -1

11. Pertama tentukan rata-rata data tersebut
𝒙 𝟎 = 𝟐𝟑
P= 5
𝒄̅ =
∑ 𝒄𝒊 𝒇𝒊
∑ 𝒇𝒊
𝒄̅ =
−𝟏
𝟏𝟎𝟎
= −𝟎, 𝟎𝟏
𝒙̅ = 𝒙 𝟎 + 𝑷𝒄̅
𝒙̅ = 𝟐𝟑 + 𝟓 (– 𝟎, 𝟎𝟏)
= 𝟐𝟑 − 𝟎, 𝟎𝟓
= 𝟐𝟐, 𝟗𝟓 (𝒅𝒊𝒃𝒖𝒍𝒂𝒕𝒌𝒂𝒏 𝒎𝒆𝒏𝒋𝒂𝒅𝒊 𝟐𝟑)
Kelas xi (𝒙𝒊 − 𝒙̅) (𝒙𝒊 − 𝒙̅) 𝟐 fi (𝒙𝒊 − 𝒙̅) 𝟐
𝐟𝐢
1-5 3 -20 400 1 400
6-10 8 -15 225 7 1575
11-15 13 -10 100 12 1200
16-20 18 -5 25 20 500
21-25 23 0 0 24 0
26-30 28 5 25 16 400
31-35 33 10 100 11 1100
36-40 38 15 225 6 1350
41-45 43 20 400 3 1200
Jumlah 100 7725
𝑺 = √
𝟏
𝒏
∑( 𝒙𝒊 − 𝒙̅) 𝟐 𝐟𝒊
𝑺 = √
𝟏
𝟏𝟎𝟎
(𝟕𝟕𝟐𝟓) = √𝟕𝟕, 𝟐𝟓 = 𝟖, 𝟖
Kelas xi (𝒙𝒊 − 𝒙̅) fi (𝒙𝒊 − 𝒙̅) 𝟒
(𝒙𝒊 − 𝒙̅) 𝟒
𝐟𝐢
1-5 3 -20 1 160000 160000
6-10 8 -15 7 50625 354357
11-15 13 -10 12 10000 120000

12. 16-20 18 -5 20 625 12500
21-25 23 0 24 0 0
26-30 28 5 16 625 10000
31-35 33 10 11 10000 110000
36-40 38 15 6 50625 303750
41-45 43 20 3 160000 480000
Jumlah 100 1550607
𝛼4 =
𝑚4
𝑆4
=
1
𝑛
∑ (𝑓𝑖( 𝑥𝑖 − 𝑥̅)4
)𝑛
𝑖=1
𝑆4
𝛼4 =
1
100
155060607
(8,8)4
𝛼4 =
1550606,07
5996,9536
𝛼4 = 2,585 = 2,6
𝛼4 < 3 𝑚𝑎𝑘𝑎 𝑘𝑢𝑟𝑣𝑎𝑛𝑦𝑎 𝑎𝑔𝑎𝑘 𝑠𝑒𝑑𝑖𝑘𝑖𝑟 𝑑𝑎𝑡𝑎𝑟 (𝑗𝑒𝑛𝑖𝑠 𝑘𝑢𝑟𝑣𝑎 𝑝𝑙𝑎𝑡𝑖𝑘𝑢𝑟𝑡𝑖𝑘).

13. Kesimpulan
Ukuran kemiringan adalah ukuran yang menyatakan sebuah model
distribusi yang mempunyai kemiringan tertentu. Apabila diketahui besarnya nilai
ukuran ini maka dapat diketahui pula bagaimana model distribusinya, apakah
distribusi itu simetrik, positif, atau negatif.
Kurtosis (ukuran keruncingan) adalah kepuncakan dari suatu distribusi,
biasanya diambil relatif terhadap distribusi normal. Dilihat dari segi
keruncingannya, kurva distribusi frekuensi dapat digolongkan menjadi tiga
golongan, yaitu : Kurva leptokurtik adalah kurva distribusi yang sangat runcing
dan nilai-nilai datanya sangat terpusat di sekitar nilai rata-rata. Kurva mesokurtik
adalah kurva yang kemiringannya sedang dan merupakan penggambaran dari
suatu distribusi normal. Kurva platikurtik adalah kurva yang betuknya mendatar
dan nilai-nilai datanya tersebar secara merata sampai jauh dari rata-ratanya.

14. Daftar Pustaka
Putri, R. I. (2012). Ukuran Kemiringan dan Ukuran Keruncingan. hal. 15.
Subana. (2000). Statistik Pendidikan. Bandung: Pustaka Setia.