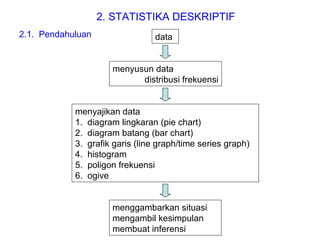
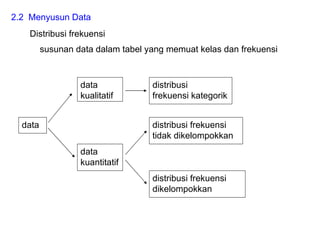
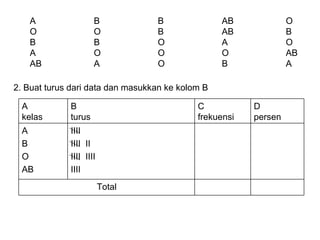
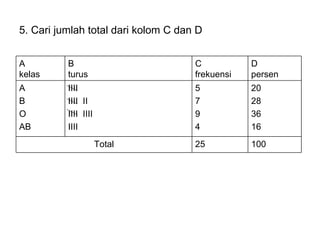
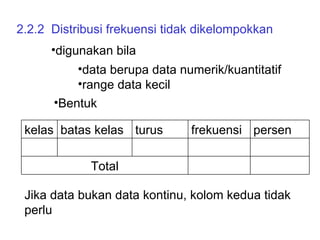
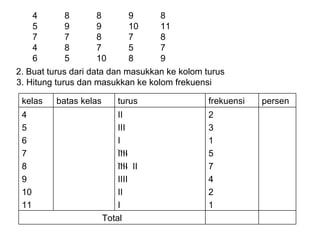
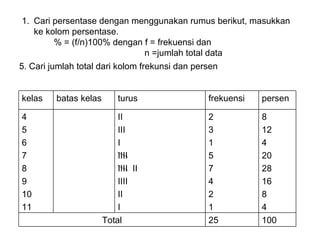
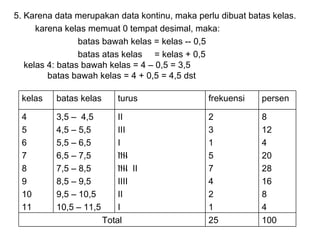
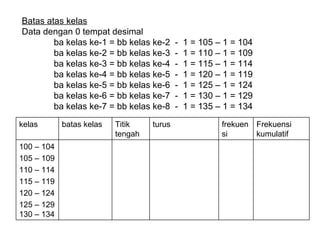
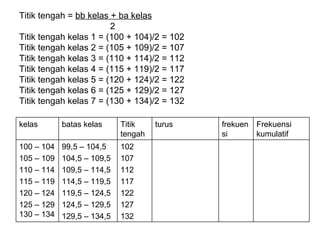
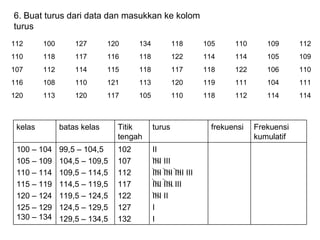
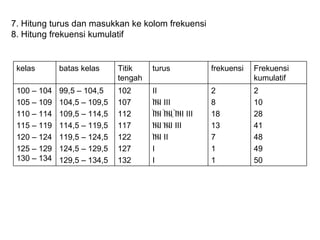
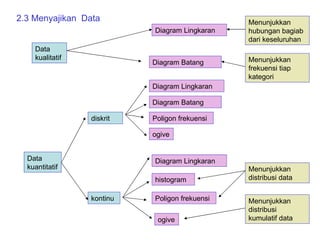
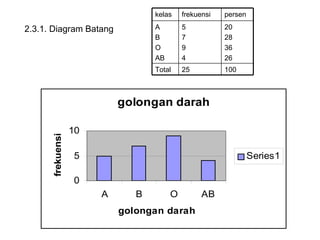
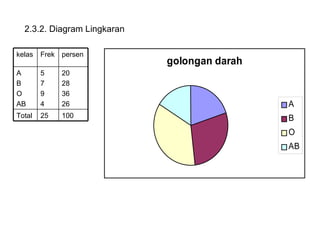
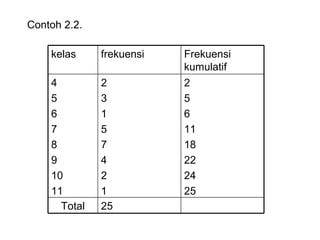
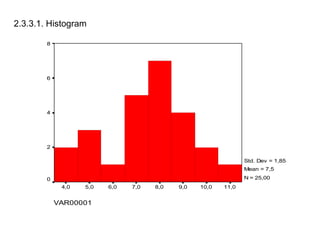
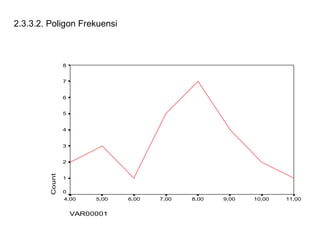
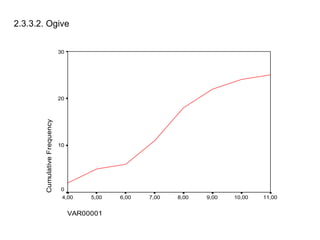
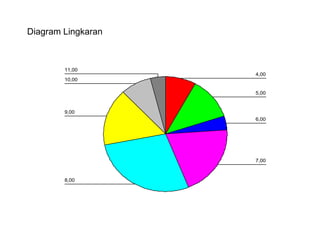
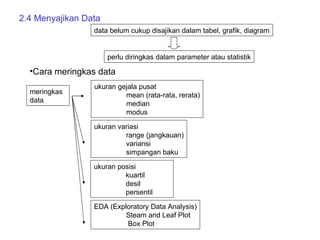
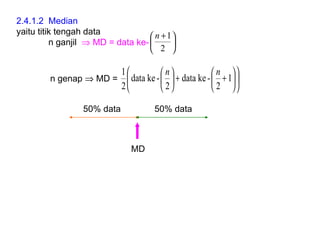
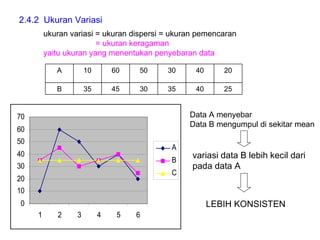
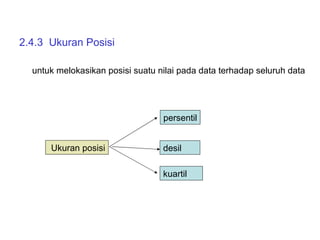
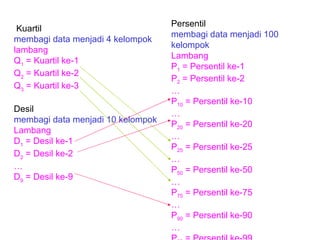
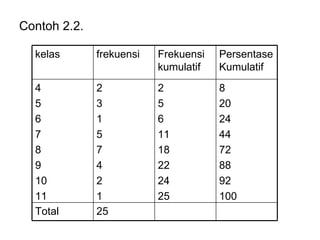
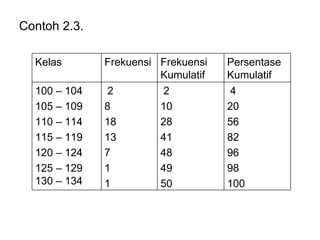
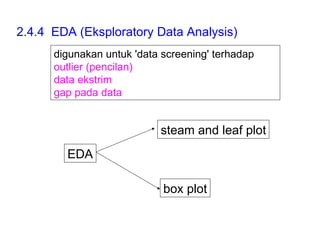
Dokumen ini membahas tentang statistika deskriptif yang mencakup cara menyusun data distribusi frekuensi dengan menggunakan berbagai bentuk visualisasi seperti diagram lingkaran, diagram batang, dan histogram. Ditegaskan bahwa distribusi frekuensi dapat digunakan untuk data kualitatif dan kuantitatif, baik yang tidak dikelompokkan maupun yang dikelompokkan sesuai kebutuhan data. Selain itu, prosedur pembuatan tabel distribusi frekuensi juga dijelaskan dengan contoh-contoh praktis terkait pengolahan data.

1. BAB II STATISTIKA DESKRIPTIF

2. 2. STATISTIKA DESKRIPTIF menggambarkan situasi mengambil kesimpulan membuat inferensi menyajikan data 1. diagram lingkaran (pie chart) 2. diagram batang (bar chart) 3. grafik garis (line graph/time series graph) 4. histogram 5. poligon frekuensi 6. ogive menyusun data distribusi frekuensi data 2.1. Pendahuluan

3. 2.2 Menyusun Data Distribusi frekuensi susunan data dalam tabel yang memuat kelas dan frekuensi data data kualitatif distribusi frekuensi kategorik data kuantitatif distribusi frekuensi tidak dikelompokkan distribusi frekuensi dikelompokkan

4. 2.2.1 Distribusi frekuensi kategorik Digunakan bila data berbentuk kategorik/kualitatif Bentuk Total persen frekuensi turus kelas

5. Contoh 2.1. Dua puluh lima orang mahasiswa dites darahnya untuk mengetahui jenis darahnya. Hasil yang diperoleh adalah sebagai berikut: A B B AB O O O B AB B B B O A O A O O O AB AB A O B A Buatlah distribusi frekuensi data tersebut!

6. Jawab: Data merupakan data kualitatif, jadi digunakan distribusi frekuensi kategorik Buat tabel seperti di bawah ini Total A B O AB D persen C frekuensi B turus A kelas

7. 2. Buat turus dari data dan masukkan ke kolom B A B B AB O O O B AB B B B O A O A O O O AB AB A O B A Total IIII IIII II IIII IIII IIII A B O AB D persen C frekuensi B turus A kelas

8. 3. Hitung turus dan masukkan ke kolom C Total 5 7 9 4 IIII IIII II IIII IIII IIII A B O AB D persen C frekuensi B turus A kelas

9. 4. Cari persentase dengan menggunakan rumus berikut, masukkan ke kolom D. % = (f/n)100% dengan f = frekuensi dan n =jumlah total data Total 20 28 36 26 5 7 9 4 IIII IIII II IIII IIII IIII A B O AB D persen C frekuensi B turus A kelas

10. 5. Cari jumlah total dari kolom C dan D 100 25 Total 20 28 36 16 5 7 9 4 IIII IIII II IIII IIII IIII A B O AB D persen C frekuensi B turus A kelas

11. 2.2.2 Distribusi frekuensi tidak dikelompokkan digunakan bila data berupa data numerik/kuantitatif range data kecil Bentuk Jika data bukan data kontinu, kolom kedua tidak perlu Total persen frekuensi turus batas kelas kelas

12. Cara mencari batas kelas 1. Jika kelas memuat 0 tempat desimal batas bawah kelas = kelas -- 0,5 batas atas kelas = kelas + 0,5 2. Jika kelas memuat 1 tempat desimal batas bawah kelas = kelas -- 0,05 batas atas kelas = kelas + 0,05 3. Jika kelas memuat 2 tempat desimal batas bawah kelas = kelas -- 0,005 batas atas kelas = kelas + 0,005

13. Contoh 2.2. Seorang psikolog memberikan tes ketrampilan pada 25 orang mahasiswa angkatan 2008. Waktu (dalam menit) yang dibutuhkan untuk menyelesaikan tes tersebut dicatat, dan diperoleh data sebagai berikut: 4 8 8 9 8 5 9 9 10 11 7 7 8 7 8 4 8 7 5 7 6 5 10 8 9 Buatlah distribusi frekuensi data tersebut!

14. Jawab: Data merupakan data kuantitatif Tentukan range data (R), yang didefinisikan sebagai berikut: R = nilai terbesar – nilai terkecil dari data di atas diperoleh: R = 11 – 4 = 7. Karena range data kecil, maka digunakan distribusi frekuensi tidak dikelompokkan dengan kelas tunggal, yaitu 4, 5, 6, 7, 8, 9, 10, 11 2. Buat tabel seperti di bawah ini: Total 4 5 6 7 8 9 10 11 persen frekuensi turus batas kelas kelas

15. 2. Buat turus dari data dan masukkan ke kolom turus 4 8 8 9 8 5 9 9 10 11 7 7 8 7 8 4 8 7 5 7 6 5 10 8 9 3. Hitung turus dan masukkan ke kolom frekuensi Total 2 3 1 5 7 4 2 1 II III I IIII IIII II IIII II I 4 5 6 7 8 9 10 11 persen frekuensi turus batas kelas kelas

16. Cari persentase dengan menggunakan rumus berikut, masukkan ke kolom persentase. % = (f/n)100% dengan f = frekuensi dan n =jumlah total data 5. Cari jumlah total dari kolom frekunsi dan persen 100 25 Total 8 12 4 20 28 16 8 4 2 3 1 5 7 4 2 1 II III I IIII IIII II IIII II I 4 5 6 7 8 9 10 11 persen frekuensi turus batas kelas kelas

17. 5. Karena data merupakan data kontinu, maka perlu dibuat batas kelas. karena kelas memuat 0 tempat desimal, maka: batas bawah kelas = kelas -- 0,5 batas atas kelas = kelas + 0,5 kelas 4: batas bawah kelas = 4 – 0,5 = 3,5 batas bawah kelas = 4 + 0,5 = 4,5 dst 100 25 Total 8 12 4 20 28 16 8 4 2 3 1 5 7 4 2 1 II III I IIII IIII II IIII II I 3,5 – 4,5 4,5 – 5,5 5,5 – 6,5 6,5 – 7,5 7,5 – 8,5 8,5 – 9,5 9,5 – 10,5 10,5 – 11,5 4 5 6 7 8 9 10 11 persen frekuensi turus batas kelas kelas

18. Bentuk lain tabel distribusi frekuensi: Frekuensi kumulatif digunakan untuk memperlihatkan nilai akumulatif lebih besar sama dengan kelas tertentu. Misalkan: 18 mahasiswa dapat menyelesaikan tes kurang dari atau sama dengan 8 menit 25 Total 0 + 2 = 2 2 + 3 = 5 5 + 1 = 6 6 + 5 = 11 11 + 7 = 18 18 + 4 = 22 22 + 2 = 24 24 + 1 = 25 2 3 1 5 7 4 2 1 II III I IIII IIII II IIII II I 3,5 – 4,5 4,5 – 5,5 5,5 – 6,5 6,5 – 7,5 7,5 – 8,5 8,5 – 9,5 9,5 – 10,5 10,5 – 11,5 4 5 6 7 8 9 10 11 Frekuensi kumulatif frekuensi turus batas kelas kelas

19. 2.2.3 Distribusi frekuensi dikelompokkan digunakan bila * data berupa data numerik/kuantitatif dan * range data besar Prosedur 1. Hitung nilai tertinggi dan terendah 2. Range = R = nilai tertinggi -- nilai terendah 3. Tentukan banyaknya kelas * pilih antara 5 -- 20 * rumus Sturges banyaknya kelas = 1 + 3,3 log n n = banyaknya data 4. Hitung lebar kelas lebar kelas = R/ (banyaknya kelas) hasilnya bulatkan ke atas

20. 5. Buat tabel bb = batas bawah; ba = batas atas Batas bawah kelas bb kelas ke-1 = titik awal (yaitu nilai terkecil atau sembarang nilai yang lebih kecil dari nilai terkecil) bb kelas ke-2 = bb kelas ke-1 + lebar kelas bb kelas ke-3 = bb kelas ke-2 + lebar kelas dst Batas atas kelas Data dengan 0 tempat desimal ba kelas ke-1 = bb kelas ke-2 - 1 ba kelas ke-2 = bb kelas ke-3 - 1 dst Titik tengah = bb kelas + ba kelas 2 = bb batas kelas + ba batas kelas 2 Frekuensi kumulatif frekuensi turus Titik tengah batas kelas kelas

21. Data dengan 1 tempat desimal ba kelas ke-1 = bb kelas ke-2 - 0,1 ba kelas ke-2 = bb kelas ke-3 - 0,1 dst Data dengan 2 tempat desimal ba kelas ke-1 = bb kelas ke-2 - 0,01 ba kelas ke-2 = bb kelas ke-3 - 0,01 dst Batas kelas Data dengan 0 tempat desimal bb batas kelas = bb kelas - 0,5 ba batas kelas = ba kelas + 0,5 Data dengan 1 tempat desimal bb batas kelas = bb kelas - 0,05 ba batas kelas = ba kelas + 0,05 Data dengan 2 tempat desimal bb batas kelas = bb kelas - 0,005 ba batas kelas = ba kelas + 0,005

22. Contoh 2.3. Data berikut ini merepresentasikan catatan temperatur tertinggi (F °) pada 50 kota. Buatlah distribusi frekuensi data tersebut! 112 100 127 120 134 118 105 110 109 112 110 118 117 116 118 122 114 114 105 109 107 112 114 115 118 117 118 122 106 110 116 108 110 121 113 120 119 111 104 111 120 113 120 117 105 110 118 112 114 114

23. Jawab: Data merupakan data kuantitatif Hitung nilai tertinggi dan terendah: Nilai tertinggi = 134, nilai terendah = 100 2. Tentukan range data: R = nilai terbesar – nilai terkeci = 134 – 100 = 34. Karena range data besar, maka digunakan distribusi frekuensi yg dikelompokkan 3. Pilih jumlah kelas yg diinginkan (biasanya antara 5 sampai 20). Pada contoh ini 7 kelas. Bisa juga menggunakan rumus Sturges banyaknya kelas = 1 + 3,3 log n , dengan n = banyaknya data 4. Hitung lebar kelas lebar kelas = R/ (banyaknya kelas) hasilnya bulatkan ke atas lebar kelas = 34/7 = 4,9 dibulatkan ke atas menjadi 5

24. 5. Buat tabel Tentukan titik awal dari kelas, bisa merupakan nilai data terkecil di kelas atau sembarang angka yang kurang dari nilai data terkecil. Misalkan di sini ditentukan mulai nilai data terkecil yaitu100. Batas bawah kelas bb kelas ke-1 = 100 bb kelas ke-2 = bb kelas ke-1 + lebar kelas = 100 + 5 = 105 bb kelas ke-3 = bb kelas ke-2 + lebar kelas = 105 + 5 = 110 bb kelas ke-4 = bb kelas ke-3 + lebar kelas = 110 + 5 = 115 bb kelas ke-5 = bb kelas ke-4 + lebar kelas = 115 + 5 = 120 bb kelas ke-6 = bb kelas ke-5 + lebar kelas = 120 + 5 = 125 bb kelas ke-7 = bb kelas ke-6 + lebar kelas = 125 + 5 = 130 Frekuensi kumulatif frekuensi turus Titik tengah batas kelas kelas

25. Batas atas kelas Data dengan 0 tempat desimal ba kelas ke-1 = bb kelas ke-2 - 1 = 105 – 1 = 104 ba kelas ke-2 = bb kelas ke-3 - 1 = 110 – 1 = 109 ba kelas ke-3 = bb kelas ke-4 - 1 = 115 – 1 = 114 ba kelas ke-4 = bb kelas ke-5 - 1 = 120 – 1 = 119 ba kelas ke-5 = bb kelas ke-6 - 1 = 125 – 1 = 124 ba kelas ke-6 = bb kelas ke-7 - 1 = 130 – 1 = 129 ba kelas ke-7 = bb kelas ke-8 - 1 = 135 – 1 = 134 100 – 104 105 – 109 110 – 114 115 – 119 120 – 124 125 – 129 130 – 134 Frekuensi kumulatif frekuensi turus Titik tengah batas kelas kelas

26. Batas kelas Data dengan 0 tempat desimal bb batas kelas = bb kelas - 0,5 ba batas kelas = ba kelas + 0,5 Pada data: bb batas kelas = bb kelas - 0,5 bb batas kelas 1 = bb kelas 1 - 0,5 = 100 – 0,5 = 99,5 bb batas kelas 2 = bb kelas 2 - 0,5 = 105 – 0,5 = 104,5 bb batas kelas 3 = bb kelas 3 - 0,5 = 110 – 0,5 = 109,5 bb batas kelas 4 = bb kelas 4 - 0,5 = 115 – 0,5 = 114,5 bb batas kelas 5 = bb kelas 5 - 0,5 = 120 – 0,5 = 119,5 bb batas kelas 6 = bb kelas 6 - 0,5 = 125 – 0,5 = 124,5 bb batas kelas 7 = bb kelas 7 - 0,5 = 130 – 0,5 = 129,5 ba batas kelas = ba kelas + 0,5 ba batas kelas 1 = ba kelas 1 + 0,5 = 104 + 0,5 = 104,5 ba batas kelas 2 = ba kelas 2 + 0,5 = 109 + 0,5 = 109,5 ba batas kelas 3 = ba kelas 3 + 0,5 = 114 + 0,5 = 114,5 ba batas kelas 4 = ba kelas 4 + 0,5 = 119 + 0,5 = 119,5 ba batas kelas 5 = ba kelas 5 + 0,5 = 124 + 0,5 = 124,5 ba batas kelas 6 = ba kelas 6 + 0,5 = 129 + 0,5 = 129,5 ba batas kelas 7 = ba kelas 1 + 0,5 = 134 + 0,5 = 134,5

27. Titik tengah = bb kelas + ba kelas 2 Titik tengah kelas 1 = (100 + 104)/2 = 102 Titik tengah kelas 2 = (105 + 109)/2 = 107 Titik tengah kelas 3 = (110 + 114)/2 = 112 Titik tengah kelas 4 = (115 + 119)/2 = 117 Titik tengah kelas 5 = (120 + 124)/2 = 122 Titik tengah kelas 6 = (125 + 129)/2 = 127 Titik tengah kelas 7 = (130 + 134)/2 = 132 102 107 112 117 122 127 132 99,5 – 104,5 104,5 – 109,5 109,5 – 114,5 114,5 – 119,5 119,5 – 124,5 124,5 – 129,5 129,5 – 134,5 100 – 104 105 – 109 110 – 114 115 – 119 120 – 124 125 – 129 130 – 134 Frekuensi kumulatif frekuensi turus Titik tengah batas kelas kelas

28. 6. Buat turus dari data dan masukkan ke kolom turus 112 100 127 120 134 118 105 110 109 112 110 118 117 116 118 122 114 114 105 109 107 112 114 115 118 117 118 122 106 110 116 108 110 121 113 120 119 111 104 111 120 113 120 117 105 110 118 112 114 114 II IIII III IIII IIII IIII III IIII IIII III IIII II I I 102 107 112 117 122 127 132 99,5 – 104,5 104,5 – 109,5 109,5 – 114,5 114,5 – 119,5 119,5 – 124,5 124,5 – 129,5 129,5 – 134,5 100 – 104 105 – 109 110 – 114 115 – 119 120 – 124 125 – 129 130 – 134 Frekuensi kumulatif frekuensi turus Titik tengah batas kelas kelas

29. 7. Hitung turus dan masukkan ke kolom frekuensi 8. Hitung frekuensi kumulatif 2 10 28 41 48 49 50 2 8 18 13 7 1 1 II IIII III IIII IIII IIII III IIII IIII III IIII II I I 102 107 112 117 122 127 132 99,5 – 104,5 104,5 – 109,5 109,5 – 114,5 114,5 – 119,5 119,5 – 124,5 124,5 – 129,5 129,5 – 134,5 100 – 104 105 – 109 110 – 114 115 – 119 120 – 124 125 – 129 130 – 134 Frekuensi kumulatif frekuensi turus Titik tengah batas kelas kelas

30. Data kualitatif Data kuantitatif Menunjukkan frekuensi tiap kategori Menunjukkan hubungan bagiab dari keseluruhan Menunjukkan distribusi data ogive Poligon frekuensi histogram Diagram Batang kontinu diskrit Diagram Lingkaran Diagram Lingkaran Diagram Batang Diagram Lingkaran Poligon frekuensi ogive Menunjukkan distribusi kumulatif data 2.3 Menyajikan Data

31. 2.3.1. Diagram Batang Persegi panjang yang lebarnya sama dan tinggi masing-masing persegi panjang menunjukkan frekuensi dari masing-masing kategori 2.3.2 Diagram lingkaran Lingkaran yg dibagi dalam bagian-bagian menurut persentase dari frekuensi masing-masing kategori 2.3.3 Histogram, poligon frekuensi, ogive Histogram: grafik yang menggambarkan data menggunakan balok vertikal yang tingginya menyatakan frekuensi Poligon frekuensi: grafik yang menggambarkan data menggunakan garis yang menghubungkan frekuensi pada titik tengah Ogive :grafik yang menggambarkan frekuensi kumulatif untuk kelas-kelas pada distribusi frekuensi

32. 2.3.1. Diagram Batang 100 25 Total 20 28 36 26 5 7 9 4 A B O AB persen frekuensi kelas

33. 2.3.2. Diagram Lingkaran 100 25 Total 20 28 36 26 5 7 9 4 A B O AB persen Frek kelas

34. Contoh 2.2. 25 Total 2 5 6 11 18 22 24 25 2 3 1 5 7 4 2 1 4 5 6 7 8 9 10 11 Frekuensi kumulatif frekuensi kelas

35. 2.3.3.1. Histogram

36. 2.3.3.2. Poligon Frekuensi

37. 2.3.3.2. Ogive

38. Diagram Lingkaran

39. 2.4 Menyajikan Data data belum cukup disajikan dalam tabel, grafik, diagram perlu diringkas dalam parameter atau statistik ukuran gejala pusat mean (rata-rata, rerata) median modus ukuran variasi range (jangkauan) variansi simpangan baku ukuran posisi kuartil desil persentil EDA (Exploratory Data Analysis) Steam and Leaf Plot Box Plot meringkas data Cara meringkas data

40. 2.4.1 Ukuran Gejala Pusat (Measures of Central Tendency) Digunakan untuk mengetahui pemusatan data Ukuran populasi : N Data populasi : x 1 , ..., x N Mean populasi :  Ukuran sampel : n Data sampel : x 1 ,...,x n Mean sampel : 2.4.1.1 Mean/Rerata/Rata-rata yaitu jumlah nilai dibagi dengan banyaknya nilai dengan  f : frekuensi kelas X m = titik tengah kelas

41. Berdasarkan contoh 2.2.: Rata-rata sampel Apabila yang diketahui adalah berupa tabel distribusi frekuensi seperti pada hasil 2.2 maka:

42. Berdasarkan contoh 2.3.: Rata-rata sampel Apabila yang diketahui adalah berupa tabel distribusi frekuensi seperti pada contoh 2.3 maka:

43. 2.4.1.2 Median yaitu titik tengah data n ganjil  MD = data ke- n genap  MD = 50% data 50% data MD

44. Berdasarkan contoh 2.2.: Data diurutkan terlebih dahulu menjadi: 4 5 5 5 6 7 7 7 7 7 8 8 8 8 8 8 8 9 9 9 9 10 10 11 Median dari data tersebut adalah: Karena n ganjil  MD = data ke- dengan Jadi median dari data tersebut adalah data ke 13 yaitu: 8 Median juga dapat diperoleh dari tabel yang telah dibuat, dengan cara melihat distribusi kumulatifnya. Pada contoh 2.2., karena telah diketahui mediannya adalah data ke-13 maka dari tabel distribusi frekuensi pada contoh 2.2. dapat diketahui bahwa data tersebut berada pada kelas 8 karena distribusi kumulatif pada kelas 7 lebih kecil dari 13 dan kelas 8 sudah lebih besar dari 13. Karena kelasnya merupakan kelas tunggal maka mediannya adalah 8

45. Berdasarkan contoh 2.3.: Data diurutkan terlebih dahulu menjadi: Median dari data tersebut adalah: dengan Jadi median dari data tersebut adalah = 100 104 105 105 105 106 107 108 109 109 110 110 110 110 110 111 111 112 112 112 112 113 113 114 114 114 114 114 115 116 116 117 117 117 118 118 118 118 118 118 119 120 120 120 120 121 122 122 127 134 Karena n genap  MD =

46. Median diperoleh rumus sebagai berikut: Median juga dapat diperoleh dari tabel distribusi frekuensi dikelompokan dengan cara membagi jumlah data (n) dengan 2 kemudian melihat lokasi data tersebut pada frekuensi kumulatifnya. Pada contoh 2.3. karena telah diketahui mediannya adalah ½ dari jumlah data yaitu 50/2 = 25 maka dari tabel distribusi frekuensi pada contoh 2.3. dapat diketahui bahwa data ke 25 pada kelas 110-114. Dengan n: jumlah data cf :frekuensi kumulatif sebelum kelas median w: lebar kelas f: frekuensi kelas median L m : batas bawah kelas dari kelas median Jadi mediannya adalah

47. 2. 4.1.3 Modus yaitu nilai yang paling sering muncul pada data Modus lebih dari Satu tidak ada Modus pada data tidak dikelompokkan dapat dilihat dari kelas yang mempunyai frekuensi terbesar. Sebagai Contoh: Pada tabel distribusi frekuensi contoh 2.2. dapat diketahui bahwa Modus dari data tersebut adalah 8 Modus pada data dikelompokkan juga dilihat dari kelas yang mempunyai frekuensi terbesar, tetapi modus pada data dikelompokkan biasanya disebut modus kelas. Sebagai Contoh: Pada tabel distribusi frekuensi contoh 2.3. dapat diketahui bahwa Modus kelas dari data tersebut adalah 110-114

48. 2.4.1.4 Midrange MR = Sebagai Contoh: Pada contoh 2.2. Midrange dari data tersebut adalah (4+11)/2= 7,5 Pada contoh 2.3. Midrange dari data tersebut adalah (100+134)/2= 117

49. 2.4.2 Ukuran Variasi ukuran variasi = ukuran dispersi = ukuran pemencaran = ukuran keragaman yaitu ukuran yang menentukan penyebaran data Data A menyebar Data B mengumpul di sekitar mean variasi data B lebih kecil dari pada data A LEBIH KONSISTEN 25 40 35 30 45 35 B 20 40 30 50 60 10 A

50. 2.4.2.1 Range/Jangkauan R = data tertinggi - data terendah Data A : R = 60 – 10 = 50 Data B : R = 45 – 25 = 20

51. 2.4.2.2 Variansi dan Simpangan Baku Variansi /ragam rata-rata kuadrat jarak dari nilai pada data ke mean Simpangan baku (Standard deviation) akar dari variansi Simpangan baku populasi Variansi populasi

52. Variansi sampel Simpangan baku sampel Dengan x i : nilai data n : ukuran sampel

53. Prosedur mencari variansi dan deviasi standar sampel untuk data dikelompokkan Buat tabel seperti di bawah ini dan cari titik tengah untuk setiap kelas 2. Kalikan frekuensi dengan titik tengah masing-masing kelas dan masukkan ke kolom D. 3. Kalikan frekuensi dengan kuadrat titik tengah masing-masing kelas dan masukkan ke kolom E 4. Jumlahkan masing-masing kolom B, D, dan E. (jumlahan kolom B adalah n, kolom D adalah  f. X m dan kolom E adalah  f. X m 2 5. Gunakan rumus 6. Akarkan s 2 untuk memperoleh simpangan baku  f. X m 2  f. X m n Total E f. X m 2 D f. X m C Titik Tengah (X m ) B Frekuensi A Kelas

54. Prosedur mencari variansi dan deviasi standar sampel untuk data tidak dikelompokkan Buat tabel seperti di bawah ini (titik tengah adalah kelas itu sendiri karena kelasnya tunggal) 2. Kalikan frekuensi dengan titik tengah masing-masing kelas dan masukkan ke kolom C. 3. Kalikan frekuensi dengan kuadrat titik tengah masing-masing kelas dan masukkan ke kolom D 4. Jumlahkan masing-masing kolom B, C, dan D. (jumlahan kolom B adalah n, kolom C adalah  f. X m dan kolom D adalah  f. X m 2 5. Gunakan rumus 6. Akarkan s 2 untuk memperoleh simpangan baku  f. X m 2  f. X m n Total D f. X m 2 C f. X m B Frekuensi A Kelas (X m )

55. 2.4.3 Ukuran Posisi untuk melokasikan posisi suatu nilai pada data terhadap seluruh data Ukuran posisi desil kuartil persentil

56. Kuartil membagi data menjadi 4 kelompok lambang Q 1 = Kuartil ke-1 Q 2 = Kuartil ke-2 Q 3 = Kuartil ke-3 Desil membagi data menjadi 10 kelompok Lambang D 1 = Desil ke-1 D 2 = Desil ke-2  D 9 = Desil ke-9 Persentil membagi data menjadi 100 kelompok Lambang P 1 = Persentil ke-1 P 2 = Persentil ke-2  P 10 = Persentil ke-10 … P 20 = Persentil ke-20 … P 25 = Persentil ke-25 … P 50 = Persentil ke-50 … P 75 = Persentil ke-75 … P 90 = Persentil ke-90 … P 99 = Persentil ke-99

57. Contoh 2.2. 25 Total 8 20 24 44 72 88 92 100 2 5 6 11 18 22 24 25 2 3 1 5 7 4 2 1 4 5 6 7 8 9 10 11 Persentase Kumulatif Frekuensi kumulatif frekuensi kelas

58. Contoh 2.3. 4 20 56 82 96 98 100 2 10 28 41 48 49 50 2 8 18 13 7 1 1 100 – 104 105 – 109 110 – 114 115 – 119 120 – 124 125 – 129 130 – 134 Persentase Kumulatif Frekuensi Kumulatif Frekuensi Kelas

59. Hubungan persentil dengan nilai X Contoh 2.4: Dari 10 tempat lokasi yang diteliti, menghasilkan jagung (dalam ton) seperti di bawah ini: 18 15 12 6 8 2 3 5 20 10 Temukan persentil rank dari 12 Data diurutkan 2 3 5 6 8 10 12 15 18 20 Pakai formula di atas untuk menemukan persentil persentil = 6 + 0,5 . 100% = 65% 10 Jadi lokasi yang menghasilkan jagung 12 ton lebih baik 65% dari lokasi lain

60. Mencari nilai yang berhubungan dengan suatu persentil Dengan menggunakan contoh di atas temukan nilai yang berhubungan dengan persentil ke 25 Karena data telah diurutkan, kemudian cari nilai dengan rumus di atas c = (10.25)/100 = 2,5 Jika nilai yang ditemukan tidak bulat maka nilai tersebut dibulatkan ke atas Maka c menjadi c = 3, jadi nilai ke 3 dari data tersebut adalah 5.

61. Dengan menggunakan contoh 2.4., temukan nilai yang berhubungan dengan persentil ke-60 Karena data telah diurutkan, kemudian cari nilai dengan rumus di atas c = (10.60)/100 = 6 Jika nilai yang ditemukan bulat, maka digunakan nilai tengah antara nilai c dan c+1. Pada kasus ini adalah antara nilai ke-6 dan ke-7 yaitu antara 10 dan 12 Maka nilai antara 10 d1n 12 adalah c = (10+12)/2 = 11, jadi nilai yang berhubungan dengan persentil ke-60 adalah 11

62. 2.4.4 EDA (Eksploratory Data Analysis) EDA steam and leaf plot box plot digunakan untuk 'data screening' terhadap outlier (pencilan) data ekstrim gap pada data

63. 2.4.4.1 Steam and leaf plot plot data yang menggunakan sebagian dari nilai data sebagai batang dan sebagian dari nilai data sebagai daun untuk membentuk kelompok Langkah: Data diurutkan Data dipisahkan menurut kelasnya Plot data

64. Dengan menggunakan contoh 2.3., langkah-langkah untuk membuat steam & leaf plot adalah sebagai berikut: Data diurutkan: 100 104 105 105 105 106 107 108 109 109 110 110 110 110 110 111 111 112 112 112 112 113 113 114 114 114 114 114 115 116 116 117 117 117 118 118 118 118 118 118 119 120 120 120 120 121 122 122 127 134 2. Data dipisahkan menurut kelasnya 100 104 105 105 105 106 107 108 109 109 110 110 110 110 110 111 111 112 112 112 112 113 113 114 114 114 114 114 115 116 116 117 117 117 118 118 118 118 118 118 119 120 120 120 120 121 122 122 127 134

65. 3. Plot data 10 10 11 11 12 12 13 steam leaf 0 4 5 5 5 6 7 8 9 9 0 0 0 0 0 1 1 2 2 2 2 3 3 4 4 4 4 4 5 6 6 7 7 7 8 8 8 8 8 8 9 0 0 0 0 1 2 2 4 7

66. 2.4.4.2 Box Plot digunakan jika data tidak banyak Langkah-langkah Data diurutkan Cari nilai terkecil Cari nilai terbesar Cari lower hinge (Q 1 ) Cari median (Q 2 ) Cari upper hinge (Q 3 ) Gambar Box Plot

67. Dengan menggunakan contoh 2.3., langkah-langkah untuk membuat box plot adalah sebagai berikut: Data diurutkan 100 104 105 105 105 106 107 108 109 109 110 110 110 110 110 111 111 112 112 112 112 113 113 114 114 114 114 114 115 116 116 117 117 117 118 118 118 118 118 118 119 120 120 120 120 121 122 122 127 134 2 . Cari nilai terkecil = 100 3. Cari nilai terbesar = 134 4. Cari lower hinge (Q 1 ); 50/4 = 12,5, Q 1 = data ke-13 = 110 5. Cari median (Q 2 ); 50/2 = 25; Q 2 = (data ke-25+data ke-26)/2 = (114+114)/2=114 6.Cari upper hinge (Q 3 ); (3/4)50 = 37,5; Q 3 = data ke-38 = 118

68. 7. Gambar Box Plot 100 130 120 110 100 110 114 118 134 Box plot juga bisa digambar secara vertikal

69. Informasi dari box plot 1. a. jika median mendekati tengah kotak, maka distribusi data mendekati simetri b. jika median berada di sebelah kiri kotak, maka distribusi data menceng ke kanan (menceng positif) c. jika median berada di sebelah kanan kotak, maka distribusi data menceng ke kiri (menceng negatif) 2. a. jika garis-garisnya mendekati sama panjangnya, maka distribusi data mendekati simetri b. jika garis sebelah kanan lebih panjang dari sebelah kiri, maka distribusi data menceng ke kanan (menceng positif) c. jika garis sebelah kiri lebih panjang dari sebelah kanan, maka distribusi data menceng ke kiri (menceng negatif)