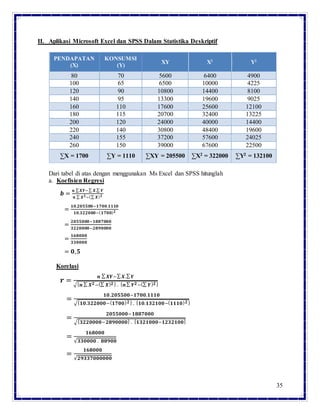
Dokumen ini membahas regresi dan korelasi sederhana dengan fokus pada definisi, analisa, serta aplikasi menggunakan alat seperti Excel dan SPSS. Terdapat berbagai pertanyaan mengenai koefisien penentuan, koefisien korelasi, dan perhitungan terkait regresi linier. Contoh perhitungan koefisien regresi dan determinasi juga disertakan untuk mendemonstrasikan penerapan teori dalam analisis data.

1. 32
Pertemuan Ke-5
REGRESI DAN KORELASI SEDERHANA
SUB POKOK BAHASAN :
4.1 Pengertian Regresi dan Korelasi
4.2 Analisa Regresi Sederhana
4.3 Analisa Korelasi Sederhana
* Aplikasi Komputer Excel dan SPSS
I. Selesaikanlah pertanyaan-pertanyaan di bawah ini dengan singkat dan jelas !
1. Hubungan antara Koefisien Penentuan dengan Koefisien Korelasi adalah ….
JAWAB : Koefisien penentuan dapat menentukan hubungan variabel
dari koefisien korelasi di mana koefisien ini menghubungkan variabel
2. Untuk menentukan berapa besar kontribusi dari X terhadap perubahan nilai Y dapat
diukur dengan ….
JAWAB : Koefisien korelasi; analisa korelasi yang digunakan untuk mengukur
kekuatan keeratan hubungan antara variabel-variabel
3. Jika keeratan hubungan antara dua variabel r = - 0,8 maka hal ini menunjukkan arah
yang ....
JAWAB : Berlawanan, X↑ maka Y↓ atau X↓ maka Y↑
4. Jika X dan Y tidak ada hubungan maka nilai r adalah .…
JAWAB : Bernilai 0
5. Jika hubungan X dan Y dinyatakan dengan fungsi linier, maka kuat tidaknya hubungan
tersebut dapat diukur dengan ….
JAWAB : Koefisien korelasi linier (r); ukuran hubungan linier antara dua
variabel atau peubah acak X dan Y untuk mengukur sejauh mana titik-titik di
sekitar sebuah garis lurus regresi
6. Rumus atau cara menghitung koefisien korelasi “r” yang benar adalah .…
JAWAB : 𝒓 =
𝒏 ∑ 𝑿𝒀−∑ 𝑿.∑ 𝒀
√{ 𝒏 ∑ 𝑿 𝟐−(∑ 𝑿) 𝟐} . { 𝒏∑ 𝒀 𝟐−(∑ 𝒀) 𝟐}
7. Persamaan garis regresi linier dinyatakan oleh ….
JAWAB : Y = a + bx
8. Rumus koefisien regresi (b) dinyatakan oleh ....
JAWAB : 𝒃 =
𝒏∑ 𝑿𝒀−∑ 𝑿.∑ 𝒀
𝒏 ∑ 𝑿 𝟐−(∑ 𝑿) 𝟐
9. Rumus intersep (a) dinyatakan oleh ....
JAWAB : 𝒂 = 𝒚̅ − 𝒃𝒙̅
10. Nilai koefisien korelasi linier (r) dinyatakan oleh ….
JAWAB : 𝒓 =
𝒏 ∑ 𝑿𝒀−∑ 𝑿.∑ 𝒀
√{ 𝒏 ∑ 𝑿 𝟐−(∑ 𝑿) 𝟐} . { 𝒏∑ 𝒀 𝟐−(∑ 𝒀) 𝟐}

2. 33
Untuk soal nomor 11 – 15 perhatikan tabel berikut ini:
PENDAPATAN
(X)
KONSUMSI
(Y)
80 70
100 65
120 90
140 95
160 110
180 115
200 120
220 140
240 155
260 150
11. Kemiringan dari garis regresi atau koefisien regresi (b) sebesar ….
JAWAB : 𝒃 =
𝒏 ∑ 𝑿𝒀−∑ 𝑿.∑ 𝒀
𝒏 ∑ 𝑿 𝟐−(∑ 𝑿) 𝟐
=
𝟏𝟎.𝟐𝟎𝟓𝟓𝟎𝟎−𝟏𝟕𝟎𝟎.𝟏𝟏𝟏𝟎
𝟏𝟎.𝟑𝟐𝟐𝟎𝟎𝟎−( 𝟏𝟕𝟎𝟎) 𝟐
=
𝟐𝟎𝟓𝟓𝟎𝟎𝟎−𝟏𝟖𝟖𝟕𝟎𝟎𝟎
𝟑𝟐𝟐𝟎𝟎𝟎𝟎−𝟐𝟖𝟗𝟎𝟎𝟎𝟎
=
𝟏𝟔𝟖𝟎𝟎𝟎
𝟑𝟑𝟎𝟎𝟎𝟎
= 𝟎, 𝟓
12. Intersep atau perpotongan garis regresi dengan sumbu Y (a) sebesar .…
JAWAB : 𝒀̅ =
∑ 𝒀
𝒏
=
𝟏𝟏𝟏𝟎
𝟏𝟎
= 𝟏𝟏𝟏
𝑿̅ =
∑ 𝑿
𝒏
=
𝟏𝟕𝟎𝟎
𝟏𝟎
= 𝟏𝟕𝟎
𝒂 = 𝒚̅ − 𝒃𝒙̅
= 𝟏𝟏𝟏 − 𝟎, 𝟓 . 𝟏𝟕𝟎
= 𝟏𝟏𝟏 − 𝟖𝟓
= 𝟐𝟔
13. Persamaan garis regresi dari data tersebut adalah ….
JAWAB : Y = a + bx
= 26 + 0,5x

3. 34
14. Koefisien korelasi linier (r) dari data tersebut sebesar ….
JAWAB : 𝒓 =
𝒏 ∑ 𝑿𝒀−∑ 𝑿.∑ 𝒀
√{ 𝒏 ∑ 𝑿 𝟐−(∑ 𝑿) 𝟐} . { 𝒏∑ 𝒀 𝟐−(∑ 𝒀) 𝟐}
=
𝟏𝟎.𝟐𝟎𝟓𝟓𝟎𝟎−𝟏𝟕𝟎𝟎.𝟏𝟏𝟏𝟎
√{ 𝟏𝟎.𝟑𝟐𝟐𝟎𝟎𝟎−( 𝟏𝟕𝟎𝟎) 𝟐} . { 𝟏𝟎.𝟏𝟑𝟐𝟏𝟎𝟎−( 𝟏𝟏𝟏𝟎) 𝟐}
=
𝟐𝟎𝟓𝟓𝟎𝟎𝟎−𝟏𝟖𝟖𝟕𝟎𝟎𝟎
√{ 𝟑𝟐𝟐𝟎𝟎𝟎𝟎−𝟐𝟖𝟗𝟎𝟎𝟎𝟎} . { 𝟏𝟑𝟐𝟏𝟎𝟎𝟎−𝟏𝟐𝟑𝟐𝟏𝟎𝟎}
=
𝟏𝟔𝟖𝟎𝟎𝟎
√𝟑𝟑𝟎𝟎𝟎𝟎 . 𝟖𝟖𝟗𝟎𝟎
=
𝟏𝟔𝟖𝟎𝟎𝟎
√𝟐𝟗𝟑𝟑𝟕𝟎𝟎𝟎𝟎𝟎𝟎
=
𝟏𝟔𝟖𝟎𝟎𝟎
𝟏𝟕𝟏𝟐𝟖𝟎,𝟒𝟕
= 𝟎, 𝟗𝟖
15. Koefisien determinasi (r2) dari data tersebut sebesar ….
JAWAB : r2 = (0,98)2
= 0,9604
16. Tentukanlah Koefisien determinasi (r2) jika diketahui koefisien korelasinya 0,94 !
JAWAB : r2 = (0,94)2
= 0,8836
17. Tentukanlah koefisien korelasinya jika nilai dari Koefisien determinasinya (r2) 0,9801 !
JAWAB : 𝒓 = √𝒓 𝟐
= √ 𝟎, 𝟗𝟖𝟎𝟏
= 𝟎, 𝟗𝟗
18. Tentukanlah koefisien korelasinya jika nilai dari Koefisien determinasinya (r2) 0,7651 !
JAWAB : 𝒓 = √𝒓 𝟐
= √𝟎, 𝟕𝟔𝟓𝟏
= 𝟎, 𝟖𝟕𝟒

4. 35
II. Aplikasi Microsoft Excel dan SPSS Dalam Statistika Deskriptif
PENDAPATAN
(X)
KONSUMSI
(Y)
XY X2
Y2
80 70 5600 6400 4900
100 65 6500 10000 4225
120 90 10800 14400 8100
140 95 13300 19600 9025
160 110 17600 25600 12100
180 115 20700 32400 13225
200 120 24000 40000 14400
220 140 30800 48400 19600
240 155 37200 57600 24025
260 150 39000 67600 22500
∑X = 1700 ∑Y = 1110 ∑XY = 205500 ∑X2 = 322000 ∑Y2 = 132100
Dari tabel di atas dengan menggunakan Ms Excel dan SPSS hitunglah
a. Koefisien Regresi
𝒃 =
𝒏 ∑ 𝑿𝒀−∑ 𝑿.∑ 𝒀
𝒏 ∑ 𝑿 𝟐−(∑ 𝑿) 𝟐
=
𝟏𝟎.𝟐𝟎𝟓𝟓𝟎𝟎−𝟏𝟕𝟎𝟎.𝟏𝟏𝟏𝟎
𝟏𝟎.𝟑𝟐𝟐𝟎𝟎𝟎−( 𝟏𝟕𝟎𝟎) 𝟐
=
𝟐𝟎𝟓𝟓𝟎𝟎𝟎−𝟏𝟖𝟖𝟕𝟎𝟎𝟎
𝟑𝟐𝟐𝟎𝟎𝟎𝟎−𝟐𝟖𝟗𝟎𝟎𝟎𝟎
=
𝟏𝟔𝟖𝟎𝟎𝟎
𝟑𝟑𝟎𝟎𝟎𝟎
= 𝟎, 𝟓
Korelasi
𝒓 =
𝒏 ∑ 𝑿𝒀−∑ 𝑿.∑ 𝒀
√{ 𝒏 ∑ 𝑿 𝟐−(∑ 𝑿) 𝟐} . { 𝒏∑ 𝒀 𝟐−(∑ 𝒀) 𝟐}
=
𝟏𝟎.𝟐𝟎𝟓𝟓𝟎𝟎−𝟏𝟕𝟎𝟎.𝟏𝟏𝟏𝟎
√{ 𝟏𝟎.𝟑𝟐𝟐𝟎𝟎𝟎−( 𝟏𝟕𝟎𝟎) 𝟐} . { 𝟏𝟎.𝟏𝟑𝟐𝟏𝟎𝟎−( 𝟏𝟏𝟏𝟎) 𝟐}
=
𝟐𝟎𝟓𝟓𝟎𝟎𝟎−𝟏𝟖𝟖𝟕𝟎𝟎𝟎
√{ 𝟑𝟐𝟐𝟎𝟎𝟎𝟎−𝟐𝟖𝟗𝟎𝟎𝟎𝟎} . { 𝟏𝟑𝟐𝟏𝟎𝟎𝟎−𝟏𝟐𝟑𝟐𝟏𝟎𝟎}
=
𝟏𝟔𝟖𝟎𝟎𝟎
√𝟑𝟑𝟎𝟎𝟎𝟎 . 𝟖𝟖𝟗𝟎𝟎
=
𝟏𝟔𝟖𝟎𝟎𝟎
√𝟐𝟗𝟑𝟑𝟕𝟎𝟎𝟎𝟎𝟎𝟎

5. 36
=
𝟏𝟔𝟖𝟎𝟎𝟎
𝟏𝟕𝟏𝟐𝟖𝟎,𝟒𝟕
= 𝟎, 𝟗𝟖
Determinasi
r2 = (0,98)2
= 0,9604
b. Persamaan Regresinya
𝒀̅ =
∑ 𝒀
𝒏
=
𝟏𝟏𝟏𝟎
𝟏𝟎
= 𝟏𝟏𝟏
𝑿̅ =
∑ 𝑿
𝒏
=
𝟏𝟕𝟎𝟎
𝟏𝟎
= 𝟏𝟕𝟎
𝒂 = 𝒚̅ − 𝒃𝒙̅
= 𝟏𝟏𝟏 − 𝟎, 𝟓 . 𝟏𝟕𝟎
= 𝟏𝟏𝟏 − 𝟖𝟓
= 𝟐𝟔
Y = a + bx
= 26 + 0,5x
TANGGAL NILAI PARAF DOSEN