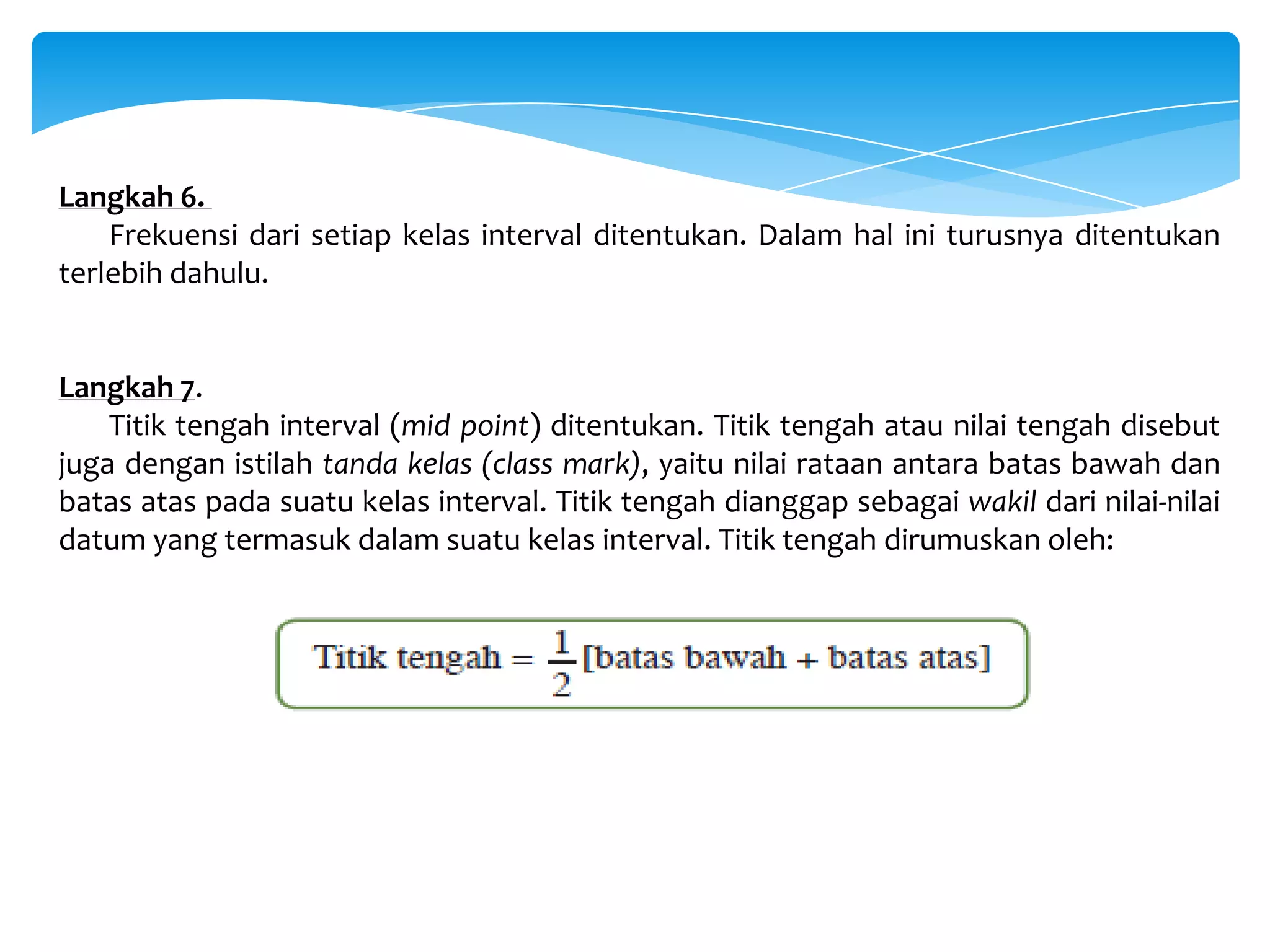
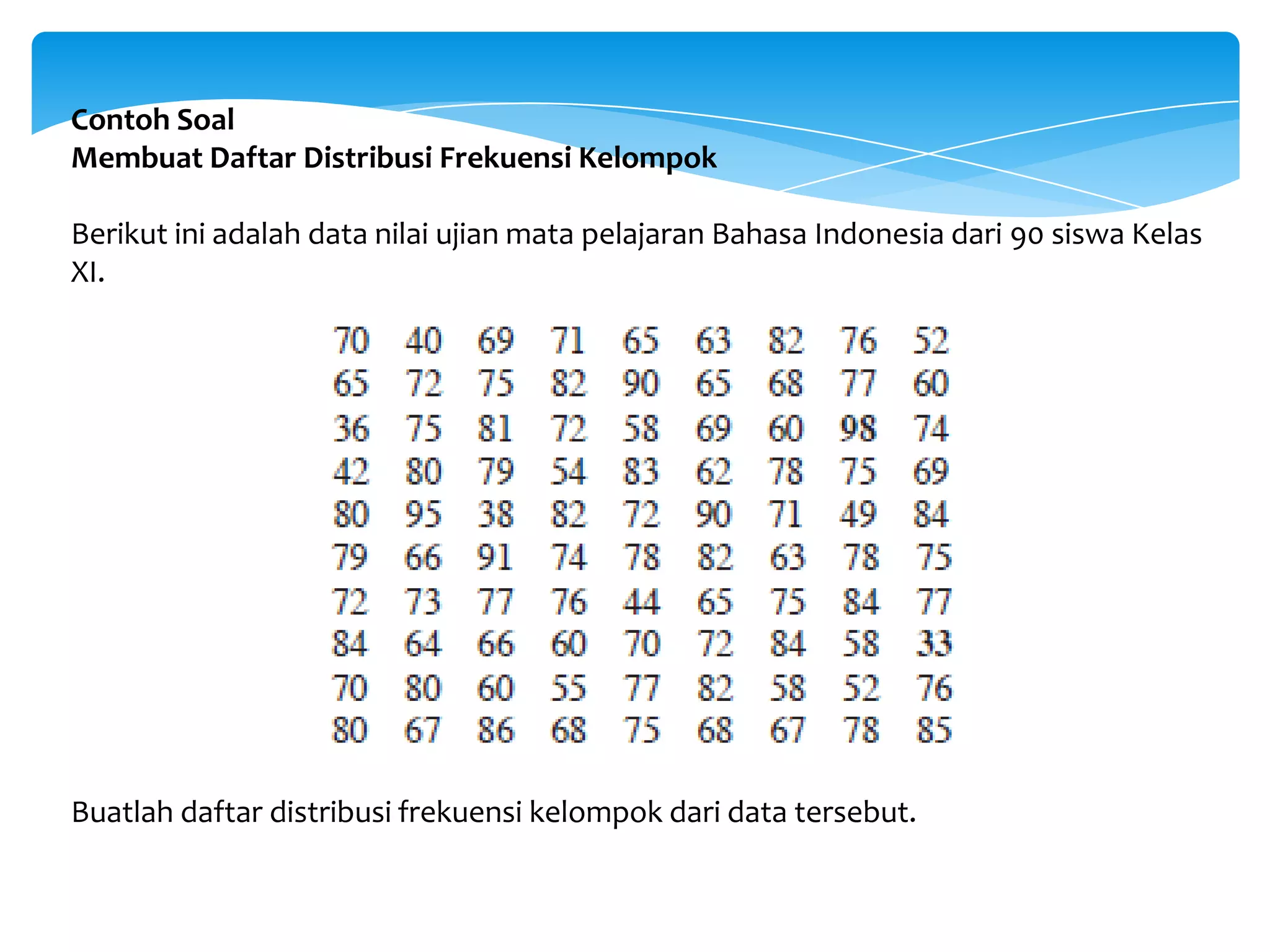
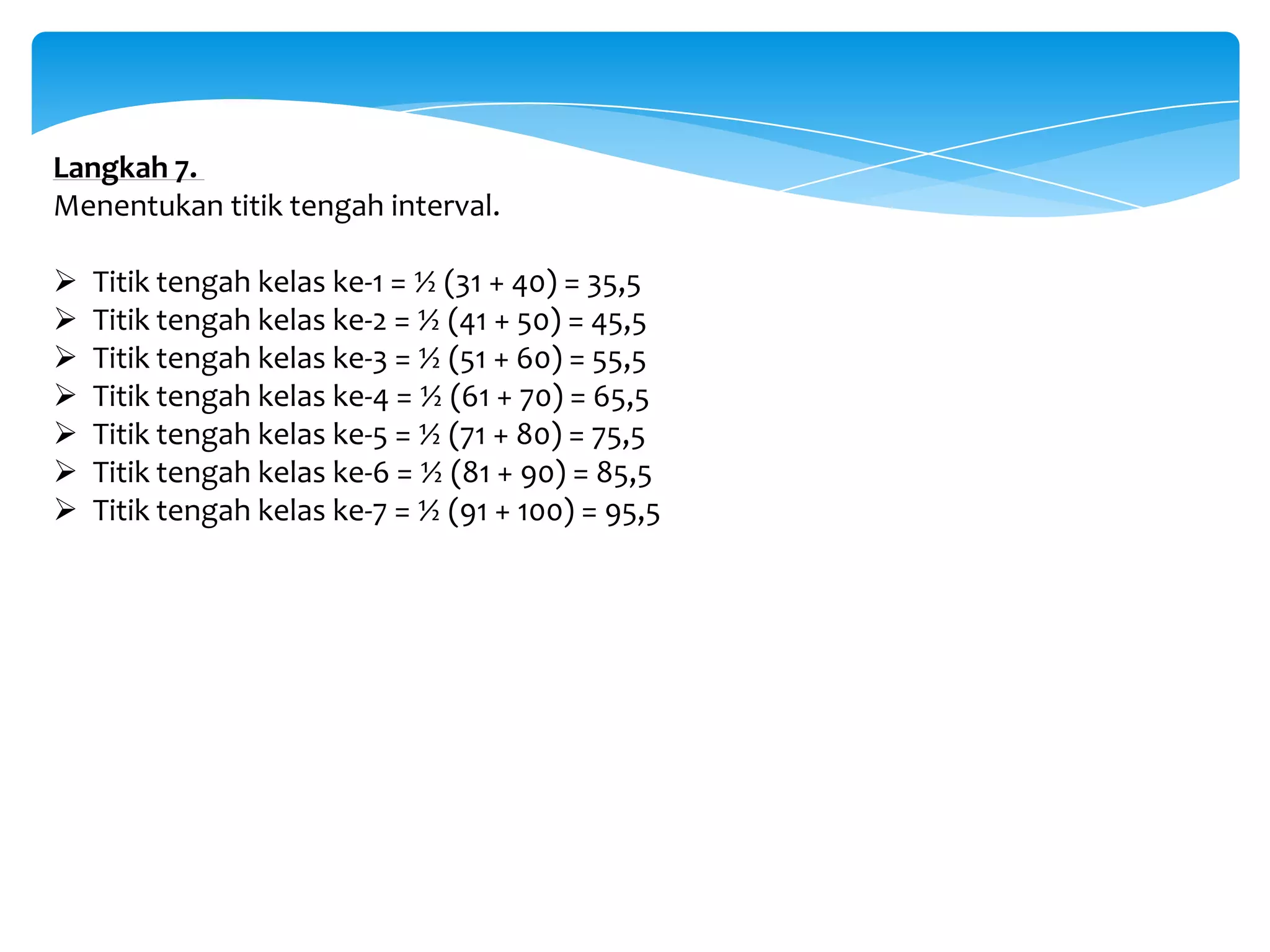
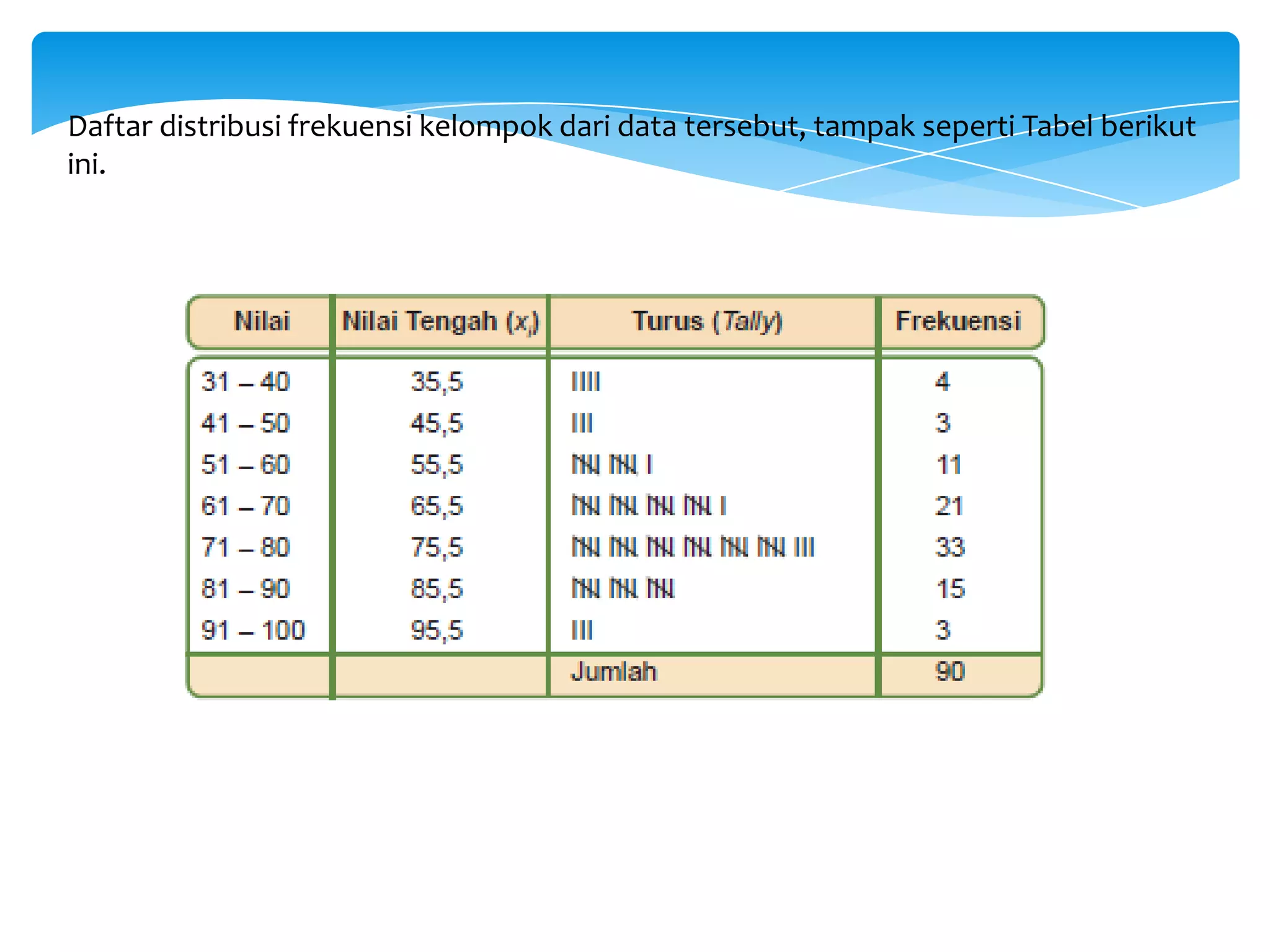
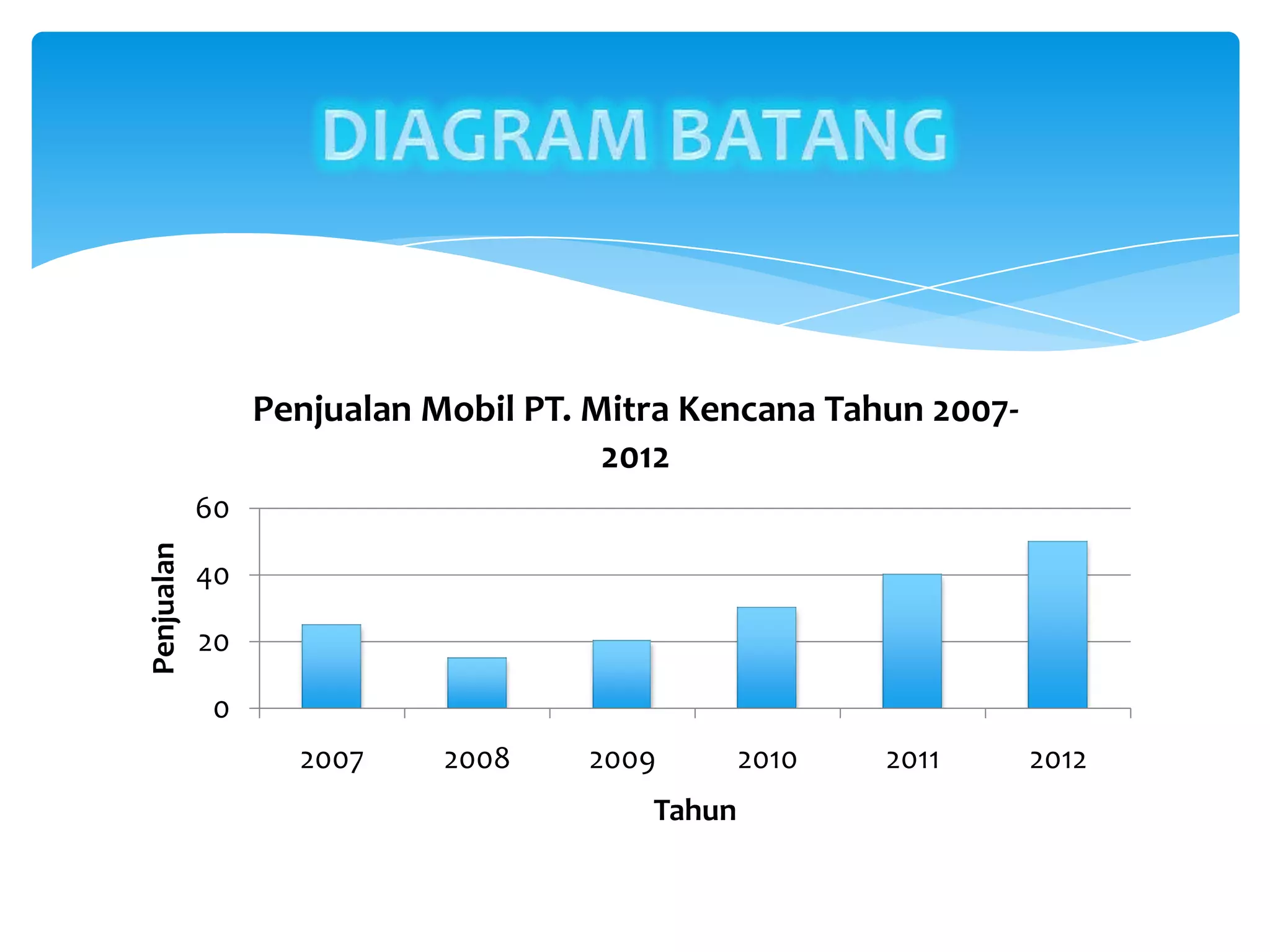
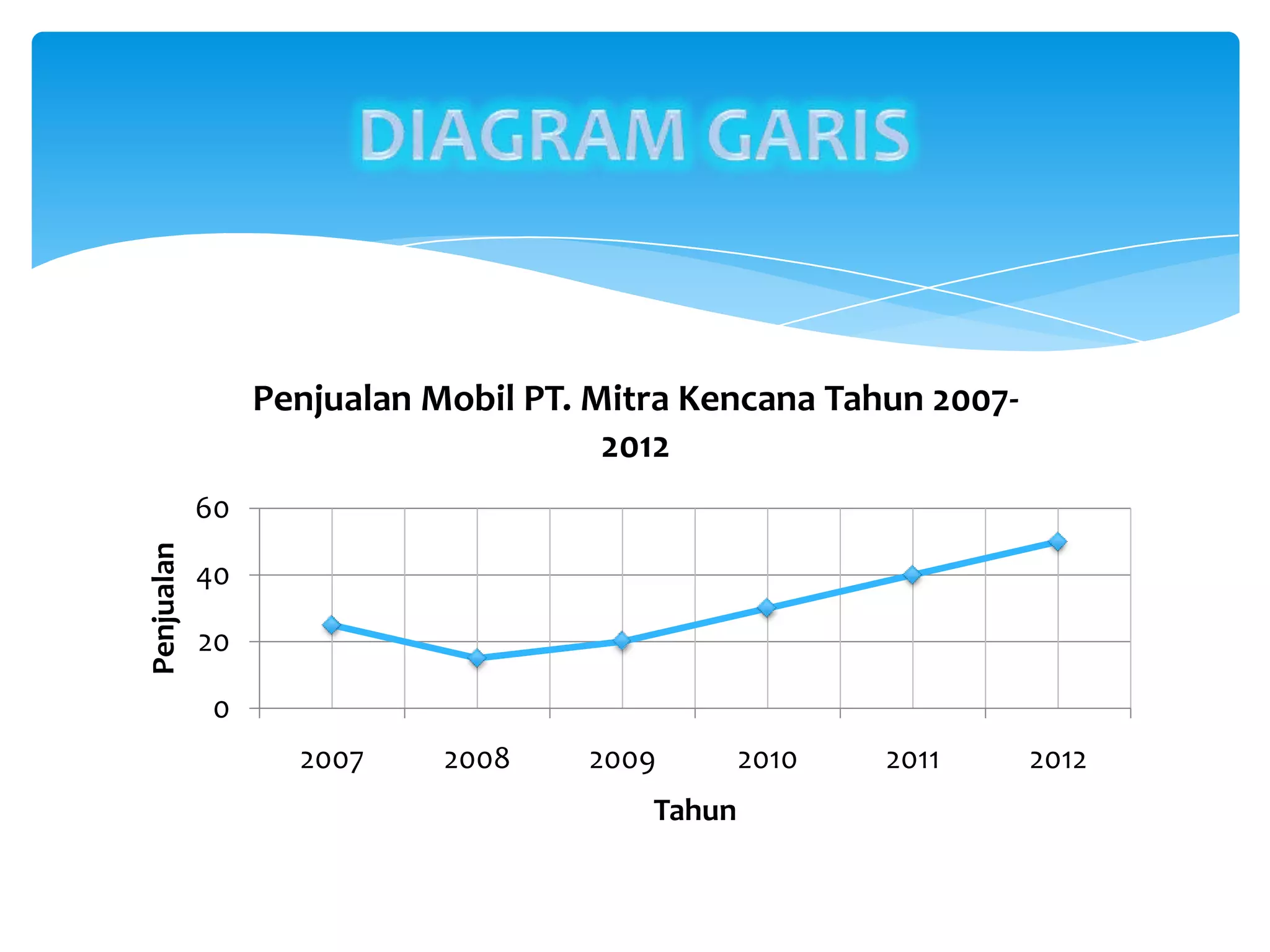
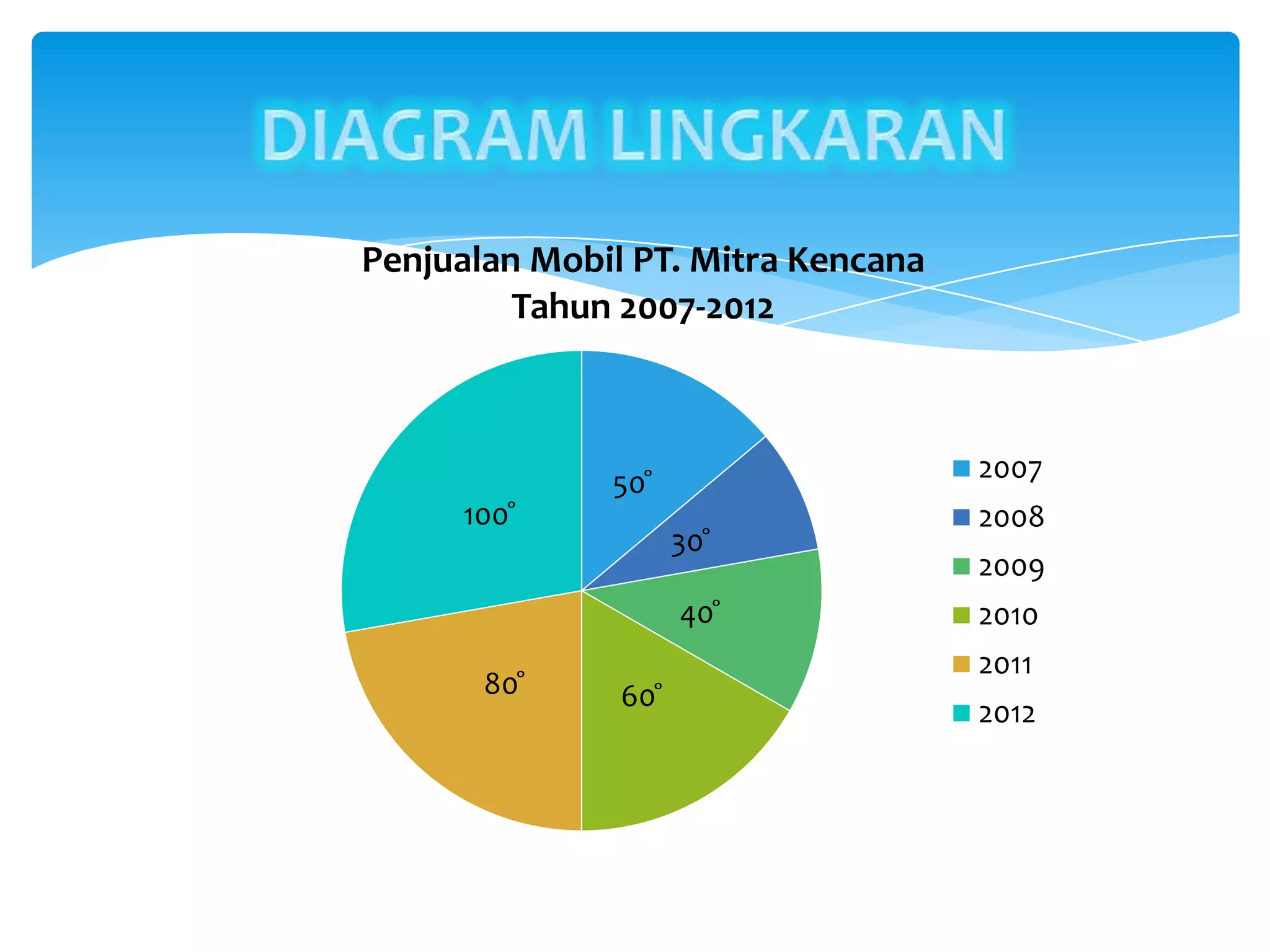
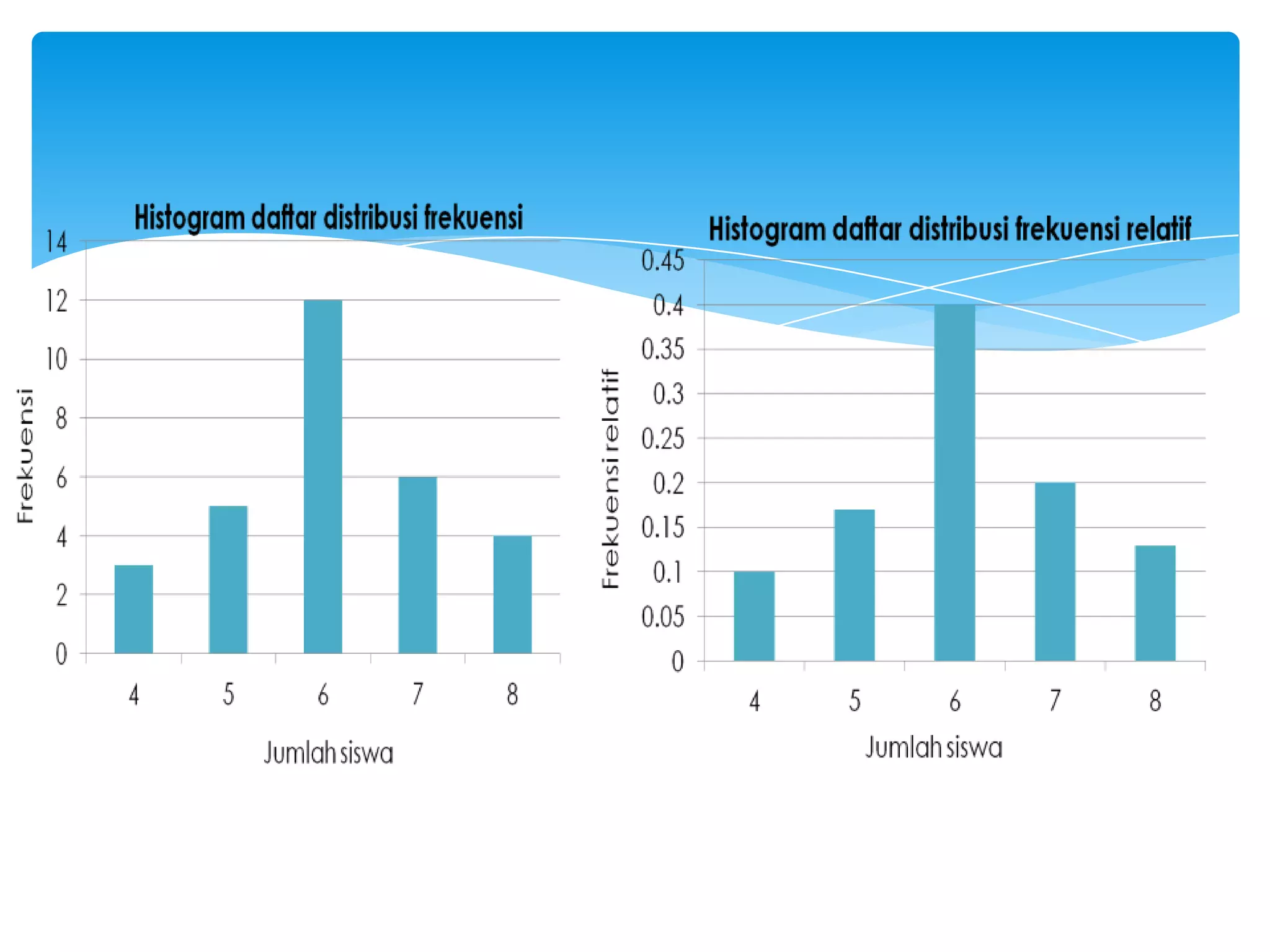
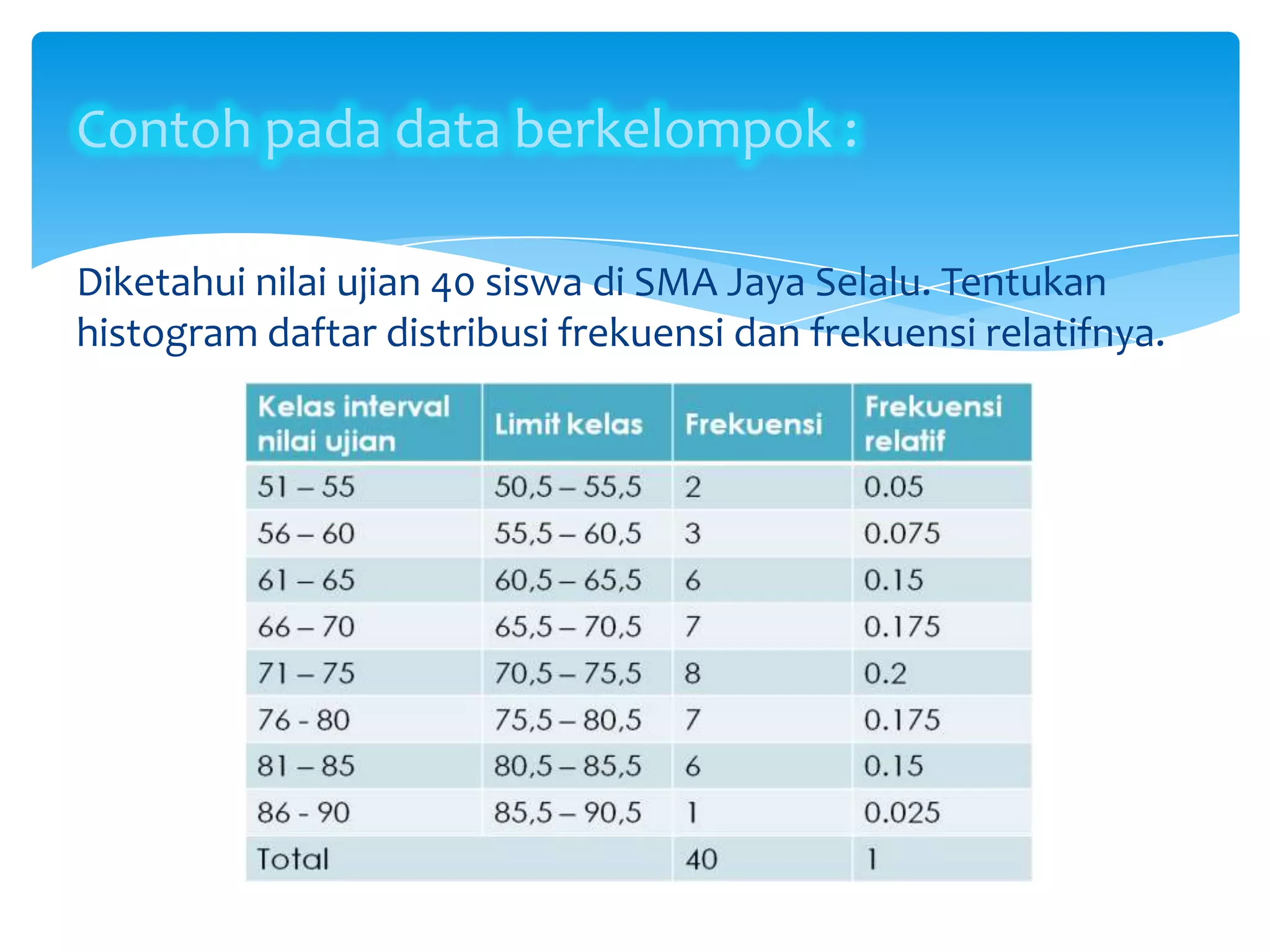
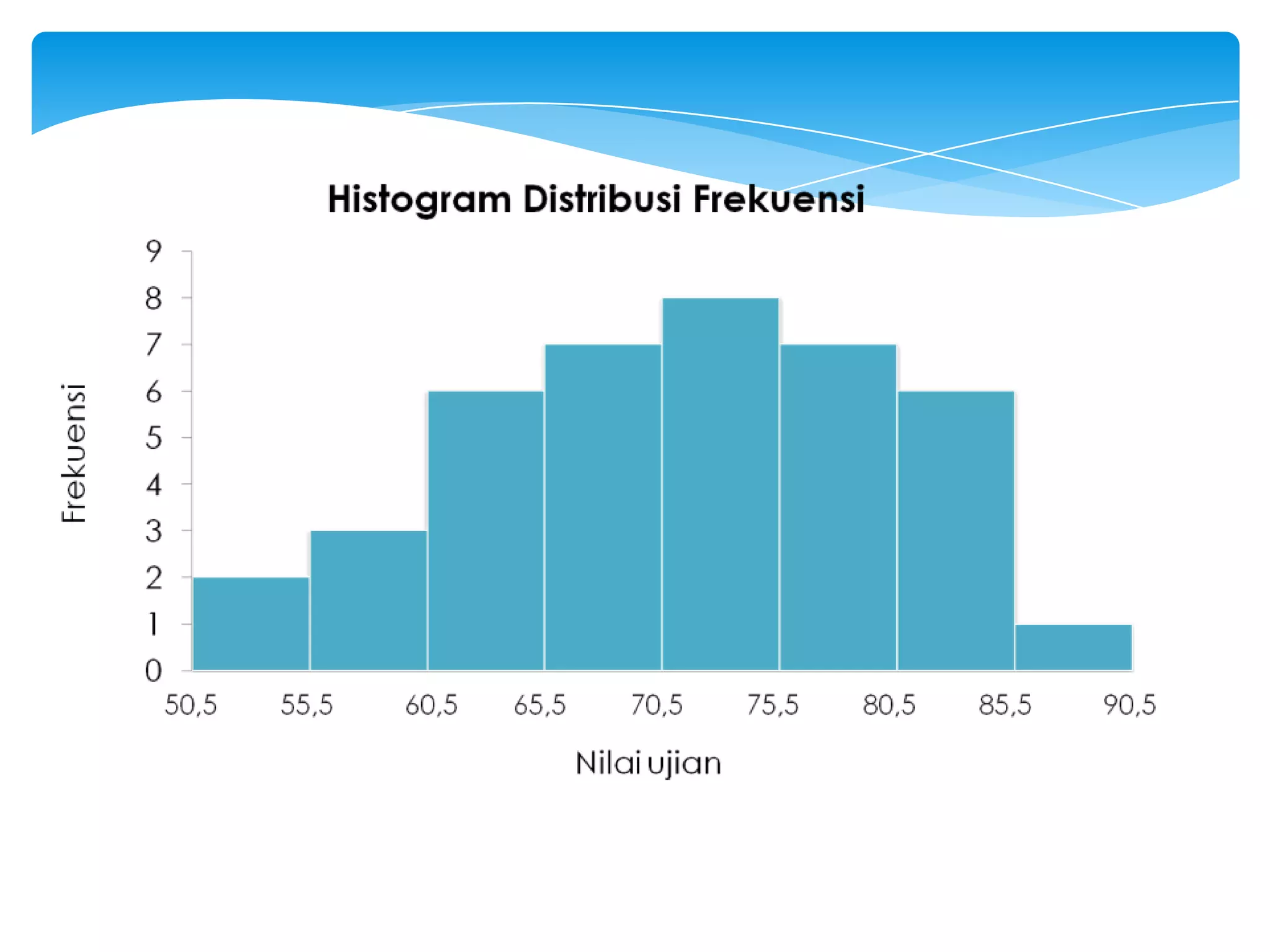
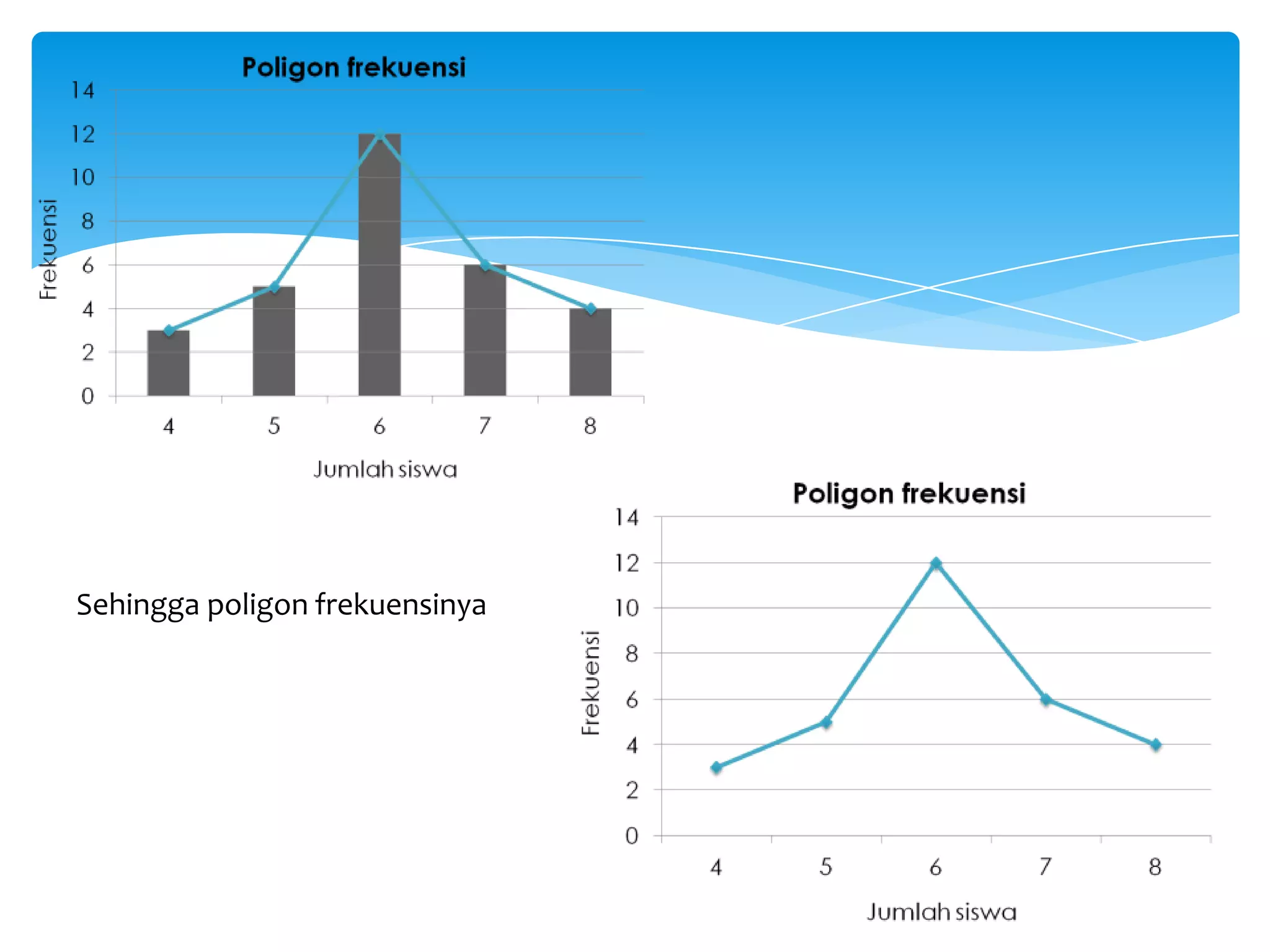
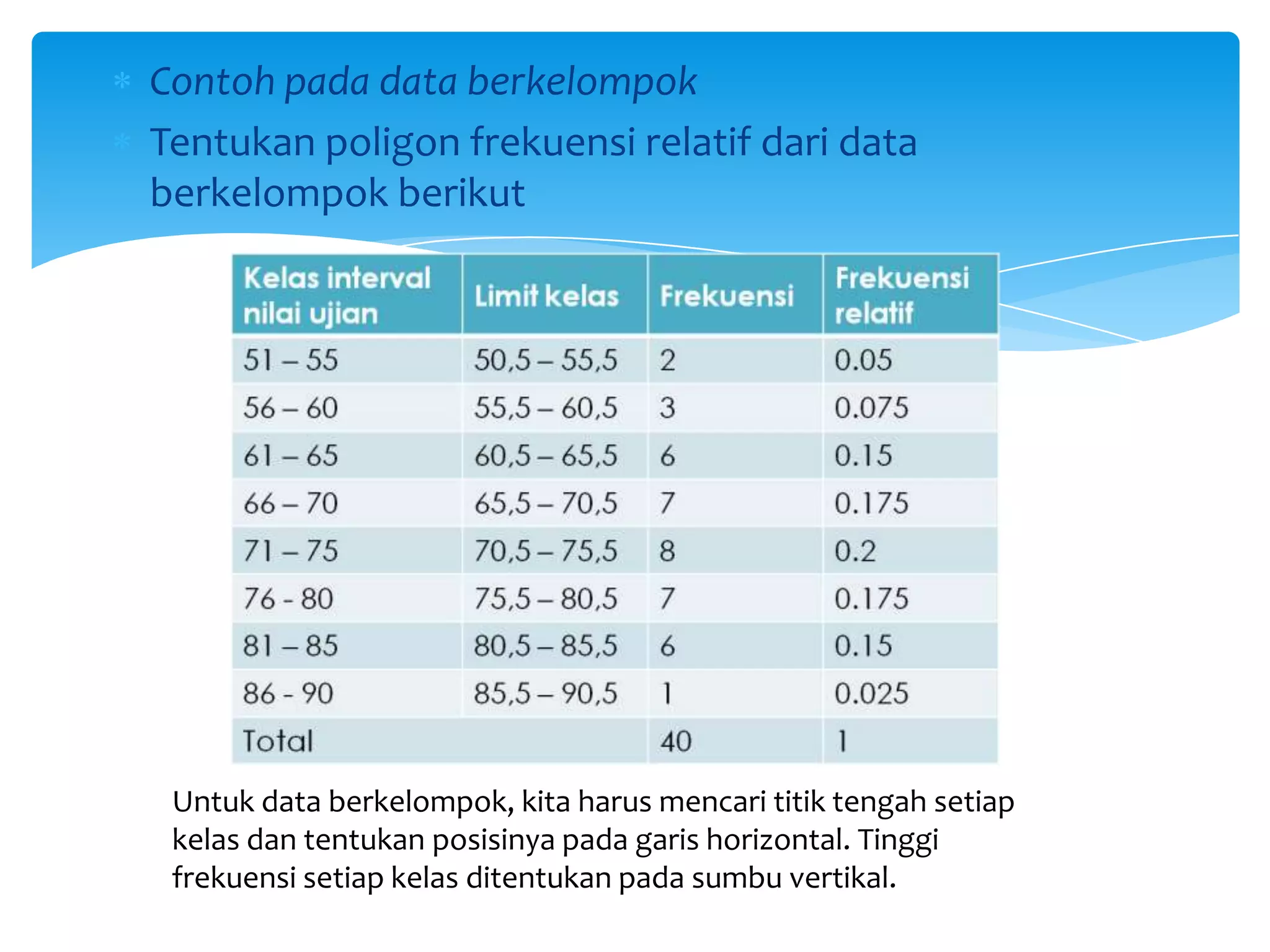
Dokumen tersebut membahas tentang statistika dan penyajian data, termasuk definisi statistika, jenis-jenis statistika, data dan datum, sampel dan populasi, serta berbagai diagram dan pola penyajian data seperti diagram batang, diagram garis, diagram lingkaran, histogram, dan poligon frekuensi.

1. Definisi Statistika dan
Penyajian Data

2. Pengertian
Statistika merupakan ilmu yang mempelajari proses
pengolahan dan analisis data hingga penarikan kesimpulan
dari data tersebut.
Sedangkan statistik merupakan hasil dari proses
pengolahan dan analisis data hingga penarikan kesimpulan
dari data dalam bentuk nilai-nilai ukuran.
Statistika

3. a) Statistika Deskriptif : Mengumpulkan data;
mengolah atau menghitung nilai-nilai ukuran data
sehingga menjadi nilai yang mudah dimengerti;
mencari maknanya; atau menyajikan data dalam
bentuk diagram.
b) Statistika Inferensi : Menggunakan pengolahan data
pada (a) untuk membuat kesimpulan atau
meramalkan hasil yang akan datang
Dalam statistika terdapat 2
kegiatan, yaitu :

4. Data merupakan sekumpulan informasi yang
didpatkan dari hasil pengamatan. Informasi yang
didapatkan tadi bisa dalam bentuk angka (seperti nilai
siswa, tinggi badan, berat badan) maupun dalam
bentuk bukan angka (seperti cita-cita: arsitek, dokter,
wiraswasta, dan sebagainya)
Datum ialah elemen-elemen yang terdapat di dalam
data. Misalnya data yang diambil ialah nilai ulangan
matematika yaitu 75, 80, 56, 93, dan 88
Datum dan Data

5. Dalam penelitian, keseluruhan objek yang diteliti disebut
populasi. Akan tetapi jika penelitian hanya melibatkan sebagian
dari keseluruhan objek yang ada, maka sebagian objek penelitian
itu disebut sampel.
Contoh:
Seorang guru akan meneliti prestasi akademis siswanya terkait
cara mengajar yang ia terapkan. Seluruh siswa yang ia ajar
berjumlah 80 siswa, tetapi sebagai dalam penelitiannya ia hanya
melibatkan 20 siswa untuk diambil datanya. Berarti dalam konteks
di atas, populasinya berjumlah 80 orang, sedangkan sampelnya
berjumlah 20 orang.
Sampel dan Populasi

6. Diagram
Batang
Garis
Lingkaran
Histogram
Poligon Frekuensi

8. Nilai Ulangan Turus Banyak Siswa
4 III 3
5 IIIII 5
6 IIIII 5
7 IIIII I 6
8 III 3
9 II 2
Data terurut:
4, 4, 4, 5, 5, 5, 5, 5, 6, 6, 6, 6, 6, 7, ,7
, 7, ,7 , 7, 7, 8, 8, 8, 9, 9

9. 0
1
2
3
4
5
6
7
4 5 6 7 8 9
BanyakSiswa
Nilai
Nilai Matematika Kelas X-9

10. Waktu 06.00 08.00 10.00 12.00 14.00 16.00 18.00
Banyak
Kendaraan
5 14 18 20 12 10 7
Banyak kendaraan yang diparkir di suatu wilayah parkir
kendaraan dicatat tiap dua jam dari pukul 06.00
sampai dengan pukul 18.00. hasil pendataannya
sebagai berikut. Buatlah diagram garis yang
menunjukkan data di atas!

11. 0
5
10
15
20
25
06.00 08.00 10.00 12.00 14.00 16.00 18.00
BanyakKendaraan
Waktu
Banyak Kendaraan di Wilayah Parkir pukul 06.00 –
18.00

12. 45 ̊
75 ̊
75 ̊
90 ̊
45 ̊
30 ̊
Nilai Matematika Kelas X-9
4
5
6
7
8
9
Nilai
Ulangan
Turus
Banyak
Siswa
4 III 3
5 IIIII 5
6 IIIII 5
7 IIIII I 6
8 III 3
9 II 2

13. Menghitung sudut pusat

14. Suatu perusahaan mobil mendata penjualan mobil
perusahaannya pada kurun waktu 2007-2012 dengan rincian:
Tahun 2007 terjual 25 mobil, tahun 2008 terjual 15 mobil, tahun
2009 terjual 20 mobil, tahun 2010 terjual 30 mobil, tahun
2011terjual 40 mobil, tahun 2012 terjual 50 mobil.
Sajikan data di atas dengan menggunakan
tabel, kemudian buatlah diagram batang, diagram garis
serta diagram lingkarannya.

15. Diskusi
1
Tabel
3
Diagram
Garis
4
Diagram
Lingkaran
2
Diagram
Batang

16. Tahun Penjualan (Frekuensi)
2007 25
2008 15
2009 20
2010 30
2011 40
2012 50

17. 0
20
40
60
2007 2008 2009 2010 2011 2012
Penjualan
Tahun
Penjualan Mobil PT. Mitra Kencana Tahun 2007-
2012

18. 0
20
40
60
2007 2008 2009 2010 2011 2012
Penjualan
Tahun
Penjualan Mobil PT. Mitra Kencana Tahun 2007-
2012

20. 50 ̊
30 ̊
40 ̊
60 ̊80 ̊
100 ̊
Penjualan Mobil PT. Mitra Kencana
Tahun 2007-2012
2007
2008
2009
2010
2011
2012

21. Histogram
Histogram adalah salah satu cara menyatakan daftar
ditribusi frekuensi atau distribusi frekuensi relatif. Pada
histogram, variable ditulis pada sumbu horizontal, dan
frekuensi (ataupun frekuensi relatif) digambarkan sebagai
panjang dari persegi panjang. Lebar persegi panjang adalah
lebar dari kelas interval sehingga antara persegi panjang yang
satu dengan yang lain tidak memiliki jarak.

22. Contoh pada data tunggal :
Tentukan histogram untuk daftar distribusi frekuensi dan
frekuensi relatifnya berdasarkan data jumlah siswa yang
terlambat masuk sekolah selama 30 hari di SMAKBO

24. Contoh pada data berkelompok :
Diketahui nilai ujian 40 siswa di SMA Jaya Selalu. Tentukan
histogram daftar distribusi frekuensi dan frekuensi relatifnya.

26. Poligon frekuensi merupakan salah satu cara untuk
menggambarkan distribusi frekuensi. Untuk memperoleh
distribusi frekuensi, kita tempatkan titik di tengah sisi lebar
dari setiap persegi panjang. Kemudian, titik-titik tersebut
dihubungkan sehingga kita memperoleh grafik garis yang kita
sebut dengan poligon frekuensi.
Contoh pada data tunggal
Tentukan poligon frekuensi dari data di bawah ini
Poligon Frekuensi

27. Sehingga poligon frekuensinya

28. Contoh pada data berkelompok
Tentukan poligon frekuensi relatif dari data
berkelompok berikut
Untuk data berkelompok, kita harus mencari titik tengah setiap
kelas dan tentukan posisinya pada garis horizontal. Tinggi
frekuensi setiap kelas ditentukan pada sumbu vertikal.

29. Langkah-langkah membuat tabel distribusi frekuensi kelompok adalah sebagai
berikut.
Langkah 1.
Jangkauan data (j) ditentukan, yaitu datum terbesar dikurangi datum terkecil.
Langkah 2.
Tentukan banyaknya kelas interval (k) yang diperlukan. Kelas interval adalah selang
interval tertentu yang membagi data menjadi beberapa kelompok. Biasanya
seorang peneliti harus mempertimbangkan banyaknya kelas interval. Umum
nya, paling sedikit 4 kelas interval sampai paling banyak 20 kelas interval. Tetapi
perlu diingat bahwa tabel distribusi kelompok digunakan untuk mengungkap atau
menekankan pola dari kelompok. Terlalu sedikit atau terlalu banyak kelas interval
akan mengaburkan pola yang ada. Jadi, peneliti yang harus menentukan.
Namun, ada suatu cara yang ditemukan oleh H. A. Sturges pada tahun 1926, yaitu
dengan rumus:

30. dengan :
k = banyak kelas berupa bilangan bulat, dan
n = banyaknya data.
Misalkan, n = 90 maka banyaknya kelas: k = 1 + 3,3 log 90 = 1 + 3,3 [1,9542] = 7,449
Oleh karena k harus bilangan bulat, banyaknya kelas adalah 7 atau 8.
Urutan kelas interval dimulai dari datum terkecil yang disusun hingga datum terbesar.
Langkah 3.
Panjang kelas interval (p) ditentukan dengan persamaan:
Nilai p harus disesuaikan dengan ketelitian data. Jika data teliti sampai
satuan, nilai p juga harus satuan. p juga harus teliti sampai satu desimal. Untuk
data yang ketelitiannya hingga satu tempat desimal,

31. Langkah 4.
Batas kelas interval (batas bawah dan batas atas) ditentu kan. Batas bawah kelas
pertama bisa diambil sama dengan nilai datum terkecil atau nilai yang lebih kecil dari
datum terkecil. Akan tetapi, selisih batas bawah dan batas atas harus kurang dari
panjang kelas. Secara umum, bilangan di sebelah kiri dari bentuk a – b, yaitu a disebut
batas bawah dan bilangan di sebelah kanannya, yaitu b disebut batas atas.
Langkah 5.
Batas bawah nyata dan batas atas nyata ditentukan. Batas bawah nyata disebut
juga tepi bawah dan batas atas nyata disebut jugatepi atas. Definisi tepi bawah dan tepi
atas adalah sebagai berikut :
Jika data teliti hingga satuan maka:
 tepi bawah = batas bawah – 0,5 dan
 tepi atas = batas atas + 0,5
Jika data teliti hingga satu tempat desimal maka:
 tepi bawah = batas bawah – 0,05 dan
 tepi atas = batas atas + 0,05
Jika data teliti hingga dua tempat desimal maka:
 tepi bawah = batas bawah – 0,005 dan
 tepi atas = batas atas + 0,005

32. Langkah 6.
Frekuensi dari setiap kelas interval ditentukan. Dalam hal ini turusnya ditentukan
terlebih dahulu.
Langkah 7.
Titik tengah interval (mid point) ditentukan. Titik tengah atau nilai tengah disebut
juga dengan istilah tanda kelas (class mark), yaitu nilai rataan antara batas bawah dan
batas atas pada suatu kelas interval. Titik tengah dianggap sebagai wakil dari nilai-nilai
datum yang termasuk dalam suatu kelas interval. Titik tengah dirumuskan oleh:

33. Contoh Soal
Membuat Daftar Distribusi Frekuensi Kelompok
Berikut ini adalah data nilai ujian mata pelajaran Bahasa Indonesia dari 90 siswa Kelas
XI.
Buatlah daftar distribusi frekuensi kelompok dari data tersebut.

34. Penyelesaian:
Langkah 1.
Datum terbesar adalah 98 dan datum terkecil adalah 33, sehingga jangkauan data:
j = xmak – xmin = 98 – 33 = 65
Langkah 2.
Banyaknya kelas interval adalah:
k = 1 + 3,3 log 90 = 1 + 3,3(1,9542) = 7,449
Untuk kasus ini, diambil kelas interval 7.
Langkah 3.
Menentukan panjang kelas interval.
p = j/k = 65/7 = 9,29 (bisa diambil 9 atau 10). Untuk contoh ini, diambil p = 10.

35. Langkah 4.
Menentukan batas kelas interval. Batas kelas ke-1 bisa diambil 33, tetapi agar kelas
interval kelihatan bagus diambil batas bawah 31, sehingga didapat batas atasnya 31 +
9 = 40.
batas kelas ke-2 = 41 – 50
batas kelas ke-3 = 51 – 60
batas kelas ke-4 = 61 – 70
batas kelas ke-5 = 71 – 80
batas kelas ke-6 = 81 – 90
batas kelas ke-7 = 91 – 100
Langkah 5.
Untuk kasus ini, Langkah 5 tidak diperlukan, tetapi langkah ini akan sangat diperlukan
pada kasus yang akan dibahas selanjutnya.
Langkah 6.
Frekuensi setiap kelas interval dapat dicari dengan menentukan turusnya terlebih
dahulu (lihat tabel Daftar Distribusi Frekuensi Kelompok dibawah ini).

36. Langkah 7.
Menentukan titik tengah interval.
 Titik tengah kelas ke-1 = ½ (31 + 40) = 35,5
 Titik tengah kelas ke-2 = ½ (41 + 50) = 45,5
 Titik tengah kelas ke-3 = ½ (51 + 60) = 55,5
 Titik tengah kelas ke-4 = ½ (61 + 70) = 65,5
 Titik tengah kelas ke-5 = ½ (71 + 80) = 75,5
 Titik tengah kelas ke-6 = ½ (81 + 90) = 85,5
 Titik tengah kelas ke-7 = ½ (91 + 100) = 95,5

37. Daftar distribusi frekuensi kelompok dari data tersebut, tampak seperti Tabel berikut
ini.

38. NEXT
TIME
YOU
SEE