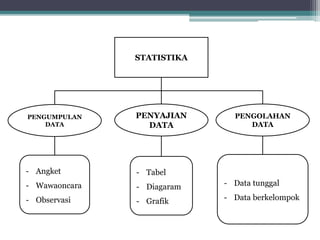
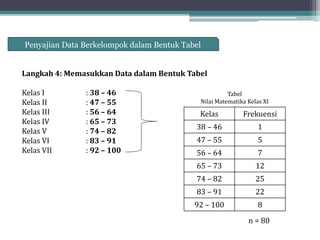
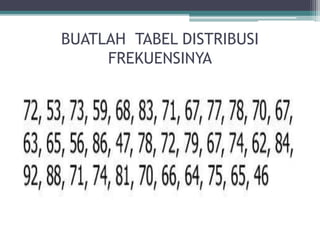
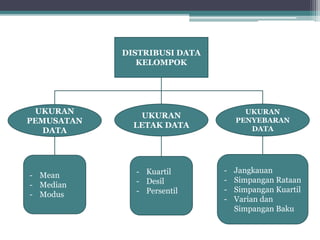
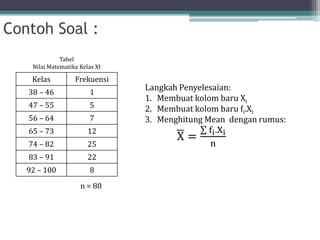
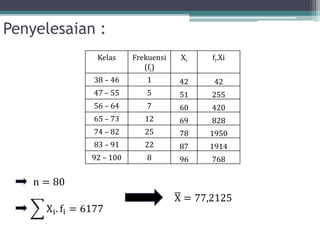
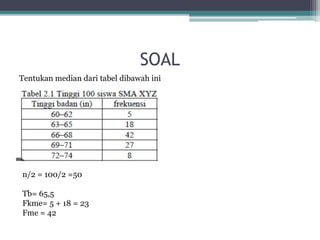
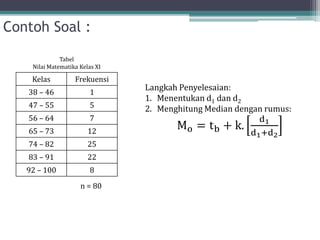
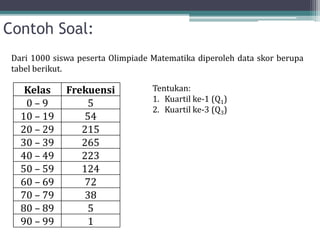
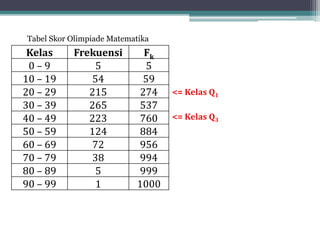
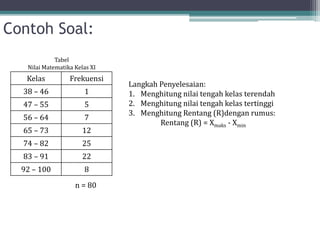
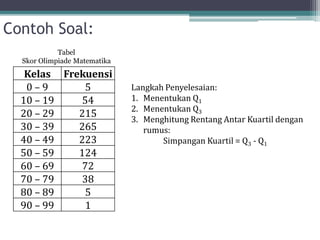
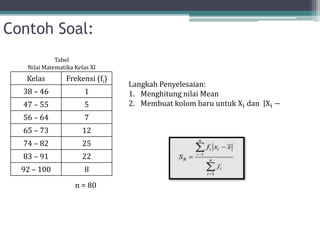
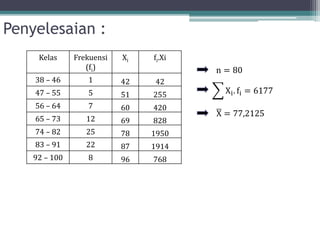
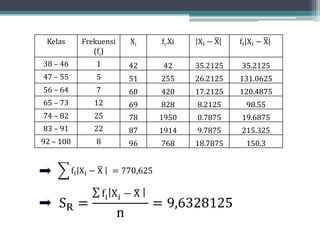
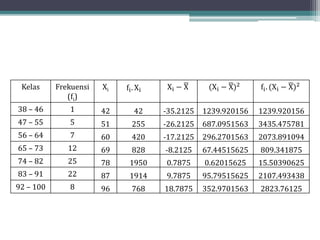
Dokumen ini membahas tentang statistika, termasuk definisi, pengumpulan, pengolahan, dan penyajian data. Penjelasan mencakup metode pembagian data menjadi kelas, serta perhitungan ukuran pemusatan dan penyebaran data seperti mean, median, modus, dan kuartil. Terdapat pula contoh penerapan dalam analisis data hasil penilaian siswa.

1. STATISTIKA
OLEH: YESY OKTAVIYANTI

2. DEFINISI
• Statistik adalah hasil pengolahan data dan
analisis data.
• Statistika adalah pengetahuan yang
berhubungan dengan cara-cara pengumpulan
data, pengolahan data, penganalisisan data, dan
penarikan kesimpulan berdasarkan kumpulan
data serta penganalisisan yang dilakukan.

3. STATISTIKA
PENGUMPULAN
DATA
PENYAJIAN
DATA
- Angket
- Wawaoncara
- Observasi
- Tabel
- Diagaram
- Grafik
PENGOLAHAN
DATA
- Data tunggal
- Data berkelompok

4. Penyajian Data Berkelompok dalam
Bentuk Tabel
Contoh Kasus:
Data hasil penilaian yang dilakukan guru matematika terhadap 80 siswa/siswi
kelas XI dinyatakan sebagai berikut:

5. Langkah 1: Mangurutkan Data Dari Data Terkecil – Data Terbesar
Penyajian Data Berkelompok dalam Bentuk Tabel

6. Langkah 2: Menentukan Banyak Kelas
Banyak Kelas dirumuskan sebagai berikut:
Berdasarkan data di atas, maka diperoleh:
𝐁𝐚𝐧𝐲𝐚𝐤 𝐊𝐞𝐥𝐚𝐬 = 𝟏 + 𝟑, 𝟑 . 𝐋𝐨𝐠 𝟖𝟎
𝐁𝐚𝐧𝐲𝐚𝐤 𝐊𝐞𝐥𝐚𝐬 = 𝟏 + 𝟑, 𝟑 . 𝟏, 𝟗𝟎𝟑
𝐁𝐚𝐧𝐲𝐚𝐤 𝐊𝐞𝐥𝐚𝐬 = 𝟕, 𝟐𝟖 ≈ 𝟕
Jadi, 80 data di atas akan dibagi menjadi 7 kelas interval.
𝐁𝐚𝐧𝐲𝐚𝐤 𝐊𝐞𝐥𝐚𝐬 = 𝟏 + 𝟑, 𝟑 . 𝐋𝐨𝐠 𝐧
Penyajian Data Berkelompok dalam Bentuk Tabel

7. Langkah 3: Menentukan Panjang Kelas
Panjang Kelas dirumuskan sebagai berikut:
Berdasarkan data di atas, maka diperoleh:
𝐁𝐚𝐧𝐲𝐚𝐤 𝐊𝐞𝐥𝐚𝐬 =
𝟔𝟎
𝟕
= 𝟖, 𝟓𝟕 ≈ 𝟖
𝐏𝐚𝐧𝐣𝐚𝐧𝐠 𝐊𝐞𝐥𝐚𝐬 =
𝐉𝐚𝐧𝐠𝐤𝐚𝐮𝐚𝐧
𝐁𝐚𝐧𝐲𝐚𝐤 𝐊𝐞𝐥𝐚𝐬
Penyajian Data Berkelompok dalam Bentuk Tabel

8. Langkah 4: Memasukkan Data dalam Bentuk Tabel
Kelas I : 38 – 46
Kelas II : 47 – 55
Kelas III : 56 – 64
Kelas IV : 65 – 73
Kelas V : 74 – 82
Kelas VI : 83 – 91
Kelas VII : 92 – 100
Penyajian Data Berkelompok dalam Bentuk Tabel
Kelas Frekuensi
38 – 46 1
47 – 55 5
56 – 64 7
65 – 73 12
74 – 82 25
83 – 91 22
92 – 100 8
n = 80
Tabel
Nilai Matematika Kelas XI

9. BUATLAH TABEL DISTRIBUSI
FREKUENSINYA

11. BENTUK UMUM:
DATA KELOMPOK (DISTRIBUSI FREKUENSI)
Interval
Titik
Tengah
(xi)
Frekuensi
(fi)
a1 – b1
a2 – b2
a3 – b3
.
.
.
an – bn
x1
x2
x3
.
.
.
xn
f1
f2
f3
.
.
.
fn
Keterangan :
ai – bi : interval (kelas) ke-i
ai : batas bawah ke-i
bi : batas atas ke-i
ai – 0,5 : tepi bawah kelas ke-i
bi – 0,5 : tepi atas kelas ke-i
(ai – 0,5) – (bi – 0,5) : panjang interval
(kelas)
xi =
ai − bi
2 : titik tengah kelas ke-i

12. DISTRIBUSI DATA
KELOMPOK
UKURAN
PEMUSATAN
DATA
UKURAN
LETAK DATA
- Mean
- Median
- Modus
- Kuartil
- Desil
- Persentil
UKURAN
PENYEBARAN
DATA
- Jangkauan
- Simpangan Rataan
- Simpangan Kuartil
- Varian dan
Simpangan Baku

13. a. Mean
b. Median
c. Modus

14. a. Mean (Rata-rata)
Keterangan:
fi : frekuensi kelas ke-i
xi : nilai tengah kelas ke-i

15. Kelas Frekuensi
38 – 46 1
47 – 55 5
56 – 64 7
65 – 73 12
74 – 82 25
83 – 91 22
92 – 100 8
n = 80
Tabel
Nilai Matematika Kelas XI
Langkah Penyelesaian:
1. Membuat kolom baru Xi
2. Membuat kolom baru fi.Xi
3. Menghitung Mean dengan rumus:
X =
fi.Xi
n
Contoh Soal :

16. Penyelesaian :
Kelas Frekuensi
(fi)
Xi fi.Xi
38 – 46 1 42 42
47 – 55 5 51 255
56 – 64 7 60 420
65 – 73 12 69 828
74 – 82 25 78 1950
83 – 91 22 87 1914
92 – 100 8 96 768
n = 80
Xi. fi = 6177
X = 77,2125

17. b. Median
Ket :
Me : Median
tb : tepi bawah kelas median
k : panjang kelas
F
: frekuensi kumulatif tepat sebelum kelas
median
fm : frekuensi kelas median
n : banyak data dari statistik terurut ∑fi

18. Contoh Soal :
Kelas Frekuensi
38 – 46 1
47 – 55 5
56 – 64 7
65 – 73 12
74 – 82 25
83 – 91 22
92 – 100 8
n = 80
Tabel
Nilai Matematika Kelas XI
Langkah Penyelesaian:
1. Menentukan kelas median dengan
rumus :
𝑛
2
2. Menghitung Median dengan rumus:
𝑀𝑒 = 𝑡𝑏 + 𝑘.
𝑛
2
−𝐹
𝑓𝑚

19. Penyelesaian :
Kelas Median =
n
2
=
80
2
= 40
Kelas Frekuensi
38 – 46 1
47 – 55 5
56 – 64 7
65 – 73 12
74 – 82 25
83 – 91 22
92 – 100 8
<= Kelas Median
𝑀𝑒 = 𝑡𝑏 + 𝑘.
𝑛
2
− 𝐹
𝑓𝑚
𝑀𝑒 = 73,5 + 8.
40 − 25
25
k = 46 − 38 = 8
𝑀𝑒 = 73,5 + 4,8
𝑀𝑒 = 12,1

20. SOAL
Tentukan median dari tabel dibawah ini
n/2 = 100/2 =50
Tb= 65,5
Fkme= 5 + 18 = 23
Fme = 42

21. c. Modus
Ket :
Mo : Modus
tb : tepi bawah kelas modus
k : panjang kelas
d1 : selisih frekuensi kelas modus dengan
kelas sebelumnya
d2 : selisih frekuensi kelas modus dengan
kelas sesudahnya

22. Contoh Soal :
Kelas Frekuensi
38 – 46 1
47 – 55 5
56 – 64 7
65 – 73 12
74 – 82 25
83 – 91 22
92 – 100 8
n = 80
Tabel
Nilai Matematika Kelas XI
Langkah Penyelesaian:
1. Menentukan d1 dan d2
2. Menghitung Median dengan rumus:
Mo = tb + k.
d1
d1+d2

23. Penyelesaian :
Kelas Frekuensi
38 – 46 1
47 – 55 5
56 – 64 7
65 – 73 12
74 – 82 25
83 – 91 22
92 – 100 8
Modus adalah nilai yang paling
sering muncul.
<=Kelas Modus
d1 = 25 − 12 = 13
d2 = 25 − 22 = 3
Mo = tb + k.
d1
d1 + d2
= 73,5 + 8.
13
13 + 3
= 73,5 + 8.
13
13 + 3
= 73,5 + 6,5
= 80

24. a. Kuartil
b. Desil
c. Persentil

25. a. Kuartil
Membagi data yang sudah diurutkan menjadi 4 bagian yang sama banyak.
Keterangan:
xmin : data terkecil
xmax : data terbesar
Q1 : kuartil ke-1
Q2 : kuartil ke-2
Q3 : kuartil ke-3

26. n : banyak data
k : panjang kelas
Qi : kuartil ke-i data, i=1,2,3
Li : tepi bawah kelas kuartil ke-i
Fq : jumlah frekuensi sebelum kuartil ke-i
Fi : frekuensi kelas yang memuat kuartil ke-i
RUMUS KUARTIL

27. Contoh Soal:
Kelas Frekuensi
0 – 9 5
10 – 19 54
20 – 29 215
30 – 39 265
40 – 49 223
50 – 59 124
60 – 69 72
70 – 79 38
80 – 89 5
90 – 99 1
Dari 1000 siswa peserta Olimpiade Matematika diperoleh data skor berupa
tabel berikut.
Tentukan:
1. Kuartil ke-1 (Q1)
2. Kuartil ke-3 (Q3)

28. Penyelesaian:
Menentukan kelas Kuartil ke-1 dan kelas Kuartil ke-3
Kelas Q1 ⇒
i
4
. n =
1
4
. 1000 = 250
Kelas Q3 ⇒
i
4
. n =
3
4
. 1000 = 750

29. Kelas Frekuensi Fk
0 – 9 5 5
10 – 19 54 59
20 – 29 215 274
30 – 39 265 537
40 – 49 223 760
50 – 59 124 884
60 – 69 72 956
70 – 79 38 994
80 – 89 5 999
90 – 99 1 1000
<= Kelas Q1
<= Kelas Q3
Tabel Skor Olimpiade Matematika

30. Li + k
i
4
. n − FQ
fq
19,5 + 9
250 − 59
54
27,49
Q1 =
=
=
Li + k
i
4
. n − FQ
fq
39,5 + 9
750 − 537
223
48,09
Q3 =
=
=

31. b. Desil
Membagi data yg urut menjadi 10 bagian yang sama banyak
Dengan demikian nilai-nilai dari desil yaitu desil ke-1 (D1), desil ke-2
(D2), desil ke-3 (D3) dan seterusnya sampai D9.
Xmaks
Xmin
D1 D2 D3 D4 D5 D6 D7 D8 D9

32. RUMUS DESIL
n : banyak data
k : panjang kelas
Di : desil ke-i data, i=1,2,3,…,9
Li : tepi bawah kelas Desil ke-i
FD : jumlah frekuensi sebelum desil ke-i
fDi
: frekuensi kelas yang memuat desil ke-i

33. c. Persentil
Membagi data yg urut menjadi 100 bagian yang sama banyak
Artinya sekumpulan data yang terurut memiliki 99 nilai presentil, yakni
P1,P2,P3,...,P99.
Xmaks
Xmin
P1 P2 P3 P4 … … … … P99

34. RUMUS PERSENTIL
n : banyak data
k : panjang kelas
Di : desil ke-i data, i=1,2,3,…,99
Li : tepi bawah kelas Persentil ke-i
FP : jumlah frekuensi sebelum persentil ke-i
fPi
: frekuensi kelas yang memuat persentil ke-i

36. a. Rentang (R)
b. Simpangan Rataan
c. Simpangan Kuartil
d. Varian (Ragam) Simpangan Baku

37. a. Rentang (R)
Range merupakan selisih antara data terbesar dengan data terkecil.
Rumus:
Keterangan:
xmaks : nilai terbesar
xmin : nilai terkecil
Jangkauan (Range) = xmaks – xmin

38. Kelas Frekuensi
38 – 46 1
47 – 55 5
56 – 64 7
65 – 73 12
74 – 82 25
83 – 91 22
92 – 100 8
n = 80
Tabel
Nilai Matematika Kelas XI
Langkah Penyelesaian:
1. Menghitung nilai tengah kelas terendah
2. Menghitung nilai tengah kelas tertinggi
3. Menghitung Rentang (R)dengan rumus:
Rentang (R) = Xmaks - Xmin
Contoh Soal:

39. Nilai tengah kelas terendah =
46+38
2
= 42
Nilai tengah kelas tertinggi =
100+92
2
= 96
Jadi,
Rentang (R) = 96 – 42= 54
<= mewakili Xmin
<= mewakili Xmaks
Penyelesaian :

40. b. Rentang Antar Kuartil (Simpangan
Kuartil)
Rentang antar kuartil merupakan selisih kuartil terbesar dengan
kuartil terkecil.
Rumus:
Keterangan:
Q1 : Kuartil Pertama
Q3 : Kuartil Ketiga
Simpangan Kuartil = Q3 – Q1

41. Contoh Soal:
Kelas Frekuensi
0 – 9 5
10 – 19 54
20 – 29 215
30 – 39 265
40 – 49 223
50 – 59 124
60 – 69 72
70 – 79 38
80 – 89 5
90 – 99 1
Tabel
Skor Olimpiade Matematika
Langkah Penyelesaian:
1. Menentukan Q1
2. Menentukan Q3
3. Menghitung Rentang Antar Kuartil dengan
rumus:
Simpangan Kuartil = Q3 - Q1

42. Penyelesaian :
Li + k
i
4
. n − FQ
fq
19,5 + 9
250 − 59
54
27,49
Q1 =
=
=
Li + k
i
4
. n − FQ
fq
39,5 + 9
750 − 537
223
48,09
Q3 =
=
=
𝑄3 − 𝑄1
48,09 − 27,49
Simpangan Kuartil =
=
= 20,6

43. c. Simpangan Rata-rata
Keterangan:
SR : Simpangan Rataan
xi : titik tengah
x : nilai rataan
fi : frekuensi kels ke-i

44. Contoh Soal:
Kelas Frekensi (fi)
38 – 46 1
47 – 55 5
56 – 64 7
65 – 73 12
74 – 82 25
83 – 91 22
92 – 100 8
n = 80
Tabel
Nilai Matematika Kelas XI
Langkah Penyelesaian:
1. Menghitung nilai Mean
2. Membuat kolom baru untuk Xi dan Xi −

45. Penyelesaian :
Kelas Frekuensi
(fi)
Xi fi.Xi
38 – 46 1 42 42
47 – 55 5 51 255
56 – 64 7 60 420
65 – 73 12 69 828
74 – 82 25 78 1950
83 – 91 22 87 1914
92 – 100 8 96 768
n = 80
Xi. fi = 6177
X = 77,2125

46. Kelas Frekuensi
(fi)
Xi fi.Xi Xi − X fi Xi − X
38 – 46 1 42 42 35.2125 35.2125
47 – 55 5 51 255 26.2125 131.0625
56 – 64 7 60 420 17.2125 120.4875
65 – 73 12 69 828 8.2125 98.55
74 – 82 25 78 1950 0.7875 19.6875
83 – 91 22 87 1914 9.7875 215.325
92 – 100 8 96 768 18.7875 150.3
fi Xi − X = 770,625
SR =
fi Xi − X
n
= 9,6328125

47. d. Varian dan Simpangan Baku
RUMUS SIMPANGAN BAKU
RUMUS VARIAN (RAGAM)
Keterangan:
SB : Simpangan Baku
SB
2 : Ragam/Varian
fi : frekuensi kelas ke-i
xi : titik tengah
x : rata-rata
n : ukuran data

48. Contoh Soal :
Kelas Frekensi (fi)
38 – 46 1
47 – 55 5
56 – 64 7
65 – 73 12
74 – 82 25
83 – 91 22
92 – 100 8
n = 80
Tabel
Nilai Matematika Kelas XI
Langkah Penyelesaian:
1. Membuat kolom baru untuk Xi, Xi − X,
(Xi − X)2, dan fi.(Xi − X)2
2. Menghitung Varian dan Simpangan Baku
dengan rumus:
Varian (Ragam) =
Simpangan Baku =
1
𝑛
𝑓𝑖. (𝑋𝑖 − 𝑋)2
1
𝑛
𝑓𝑖. (𝑋𝑖 − 𝑋)2

49. Penyelesaian :
Kelas Frekuensi
(fi)
Xi fi.Xi
38 – 46 1 42 42
47 – 55 5 51 255
56 – 64 7 60 420
65 – 73 12 69 828
74 – 82 25 78 1950
83 – 91 22 87 1914
92 – 100 8 96 768
n = 80
Xi. fi = 6177
X = 77,2125

50. Kelas Frekuensi
(fi)
Xi Xi − X (Xi − X)2 fi. (Xi − X)2
38 – 46 1 42 42 -35.2125 1239.920156 1239.920156
47 – 55 5 51 255 -26.2125 687.0951563 3435.475781
56 – 64 7 60 420 -17.2125 296.2701563 2073.891094
65 – 73 12 69 828 -8.2125 67.44515625 809.341875
74 – 82 25 78 1950 0.7875 0.62015625 15.50390625
83 – 91 22 87 1914 9.7875 95.79515625 2107.493438
92 – 100 8 96 768 18.7875 352.9701563 2823.76125
fi. Xi

51. Varian (Ragam) =
=
=
Simpangan Baku=
=
= 12,50269346
1
𝑛
𝑓𝑖. (𝑋𝑖 − 𝑋)2
1
80
(12505,3875)
156,3173438
1
𝑛
𝑓𝑖. (𝑋𝑖 − 𝑋)2
156,3173438

52. Terima Kasih . . . .