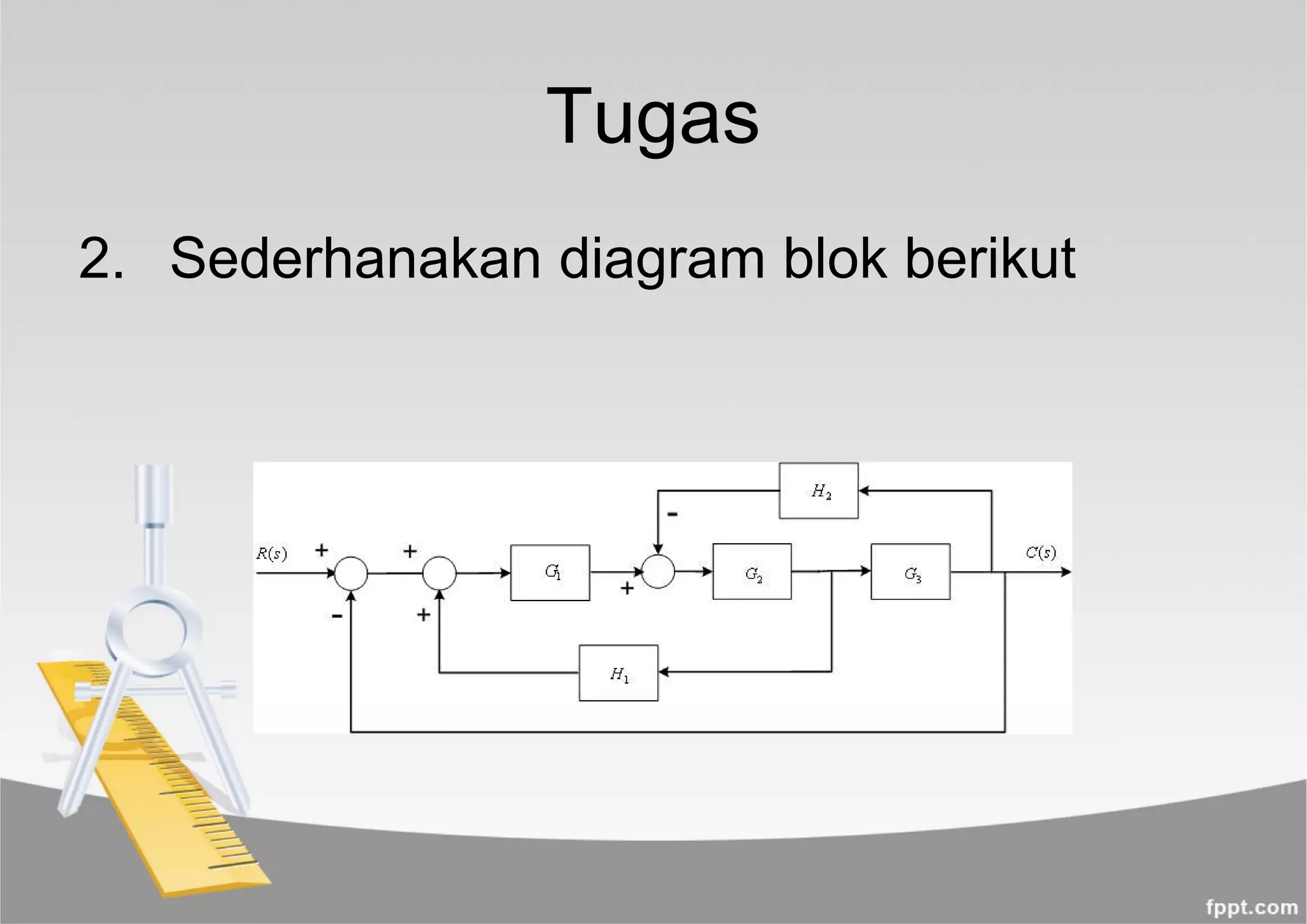
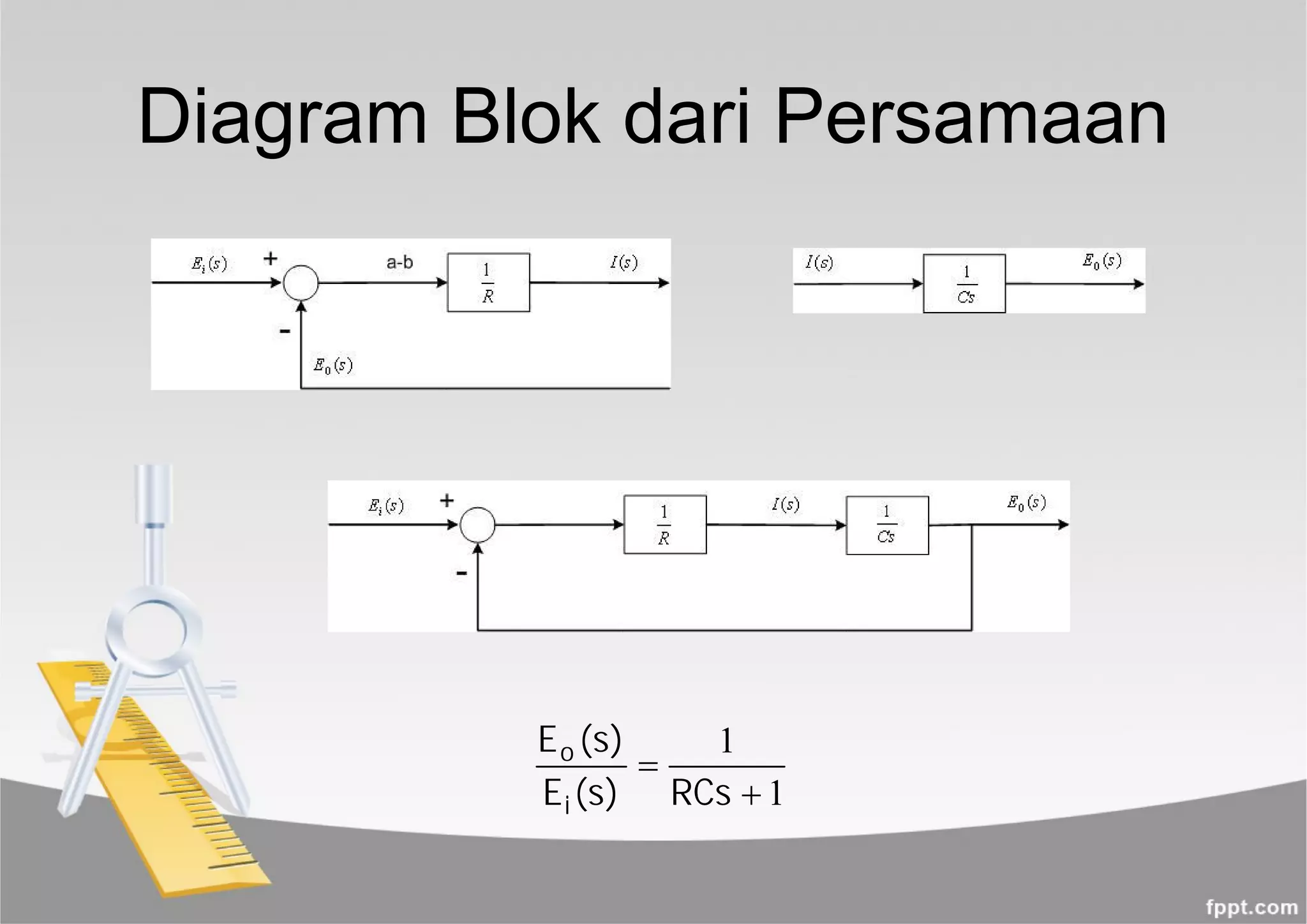
Dokumen ini membahas sistem kendali otomatis dan fungsi alih melalui persamaan matematis yang menggambarkan hubungan antara input dan output. Juga dijelaskan penggunaan transformasi Laplace, diagram blok, serta contoh solusi persamaan diferensial untuk sistem terkendali. Penjelasan mencakup representasi diagram blok dan fungsi transfer baik dalam sistem terbuka maupun tertutup.





![6
)2)(1(
5
)23(
5
)(
2
2
2
sss
ss
sss
ss
sY
2
3
)1(
5
)]()2[(
5
)2(
5
)]()1[(
2
5
)2)(1(
5
)]([
2
2
2
1
2
0
ss
ss
sYsC
ss
ss
sYsB
ss
ss
ssYA
s
s
s
Invers transformasi Laplace dilakukan dengan memanipulasi penyebut (denumerator)
dalam fungsi Y(s) kedalam akar-akarnya:
)2)(1(
5
)2()1(
)(
2
sss
ss
s
C
s
B
s
A
sY
Ekpansi dalam pecahan parsial,
Dimana A, B dan C adalah koefisien](https://image.slidesharecdn.com/diagram-blok-190420153457/75/Diagram-blok-6-2048.jpg)

![9
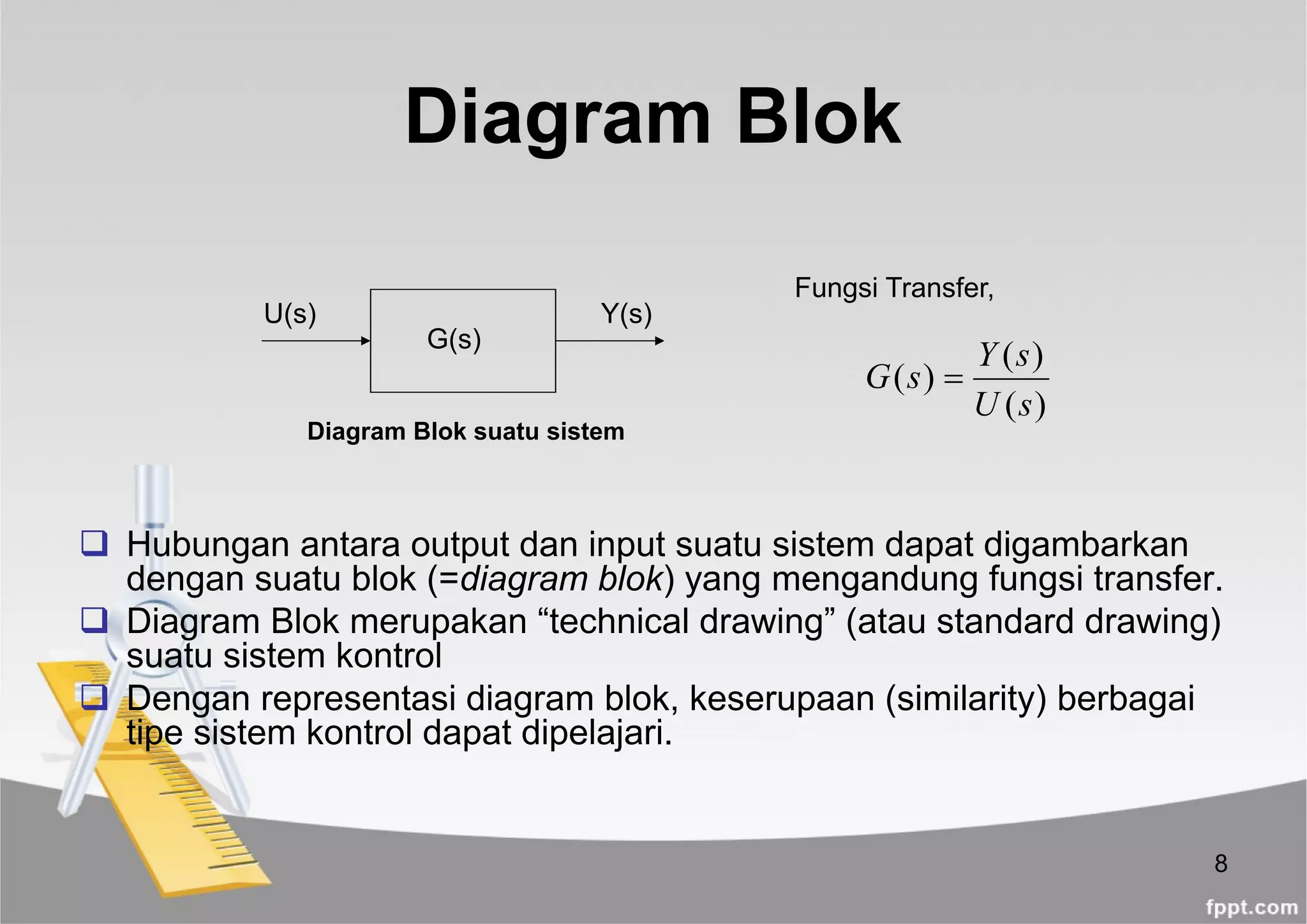
Diagram Blok sistem tertutup:
Ideal
G(s)
E(s) Y(s)
-
+
H(s)
R(s)
B(s)
Titik Penjumlahan
Titik Percabangan
R(s)=Referensi sinyal input
E(s)=Sinyal error [E(s)=R(s)-B(s)]
G(s), H(s)=Fungsi Transfer
B(s)= Sinyal feedback
Y(s)=Sinyal output](https://image.slidesharecdn.com/diagram-blok-190420153457/75/Diagram-blok-9-2048.jpg)
![10
)(
)(
)(
sG
sE
sY
FFTF
)()(
)(
)(
sHsG
sE
sB
OLTF
)()(1
)(
)(
)(
sHsG
sG
sR
sY
CLTF
)(
)()(1
)(
)( sR
sHsG
sG
sY
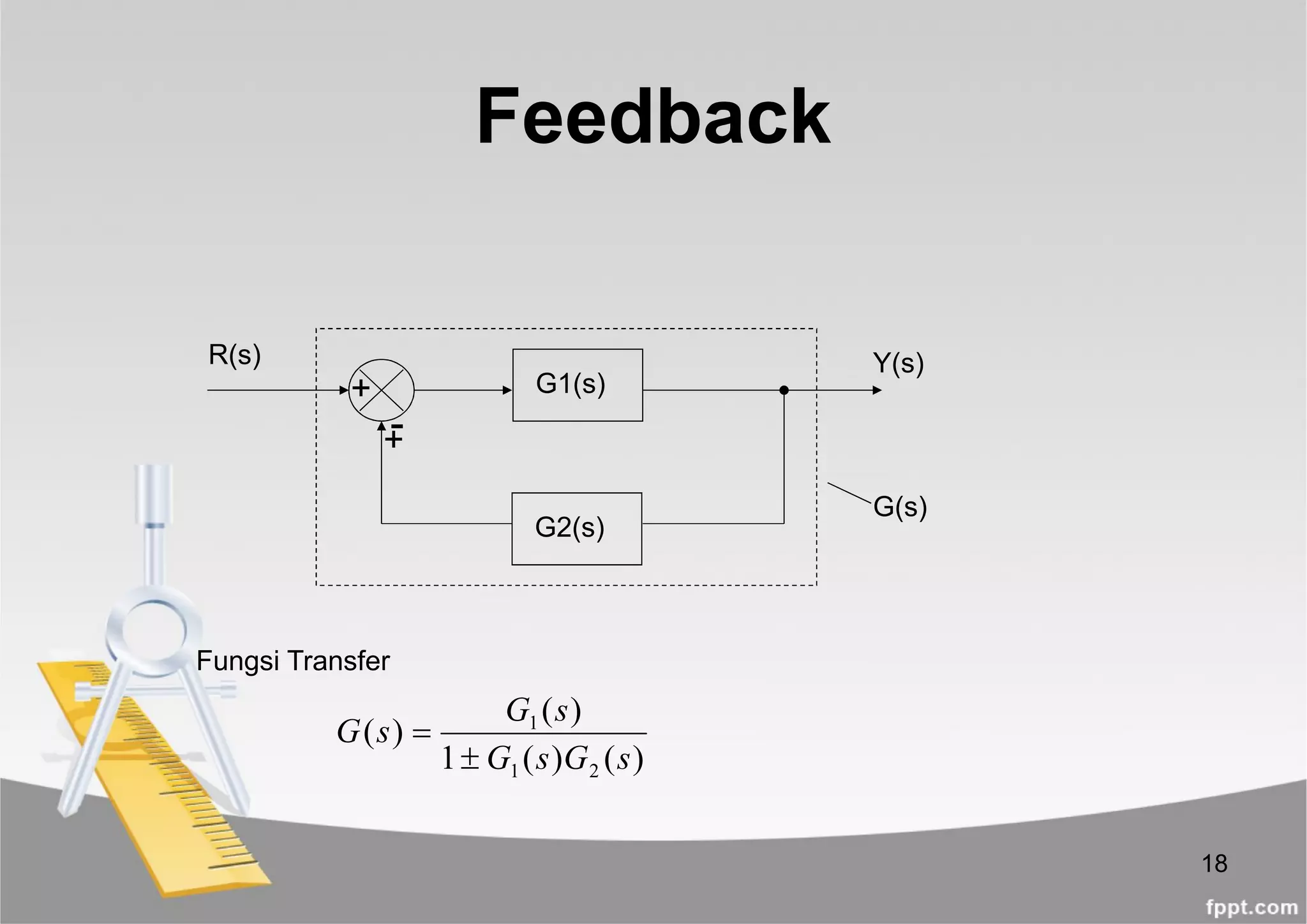
Feed-forward Transfer Function, FFTF
Open-Loop Transfer Function, OLTF
Closed-Loop Transfer Function, CLTF
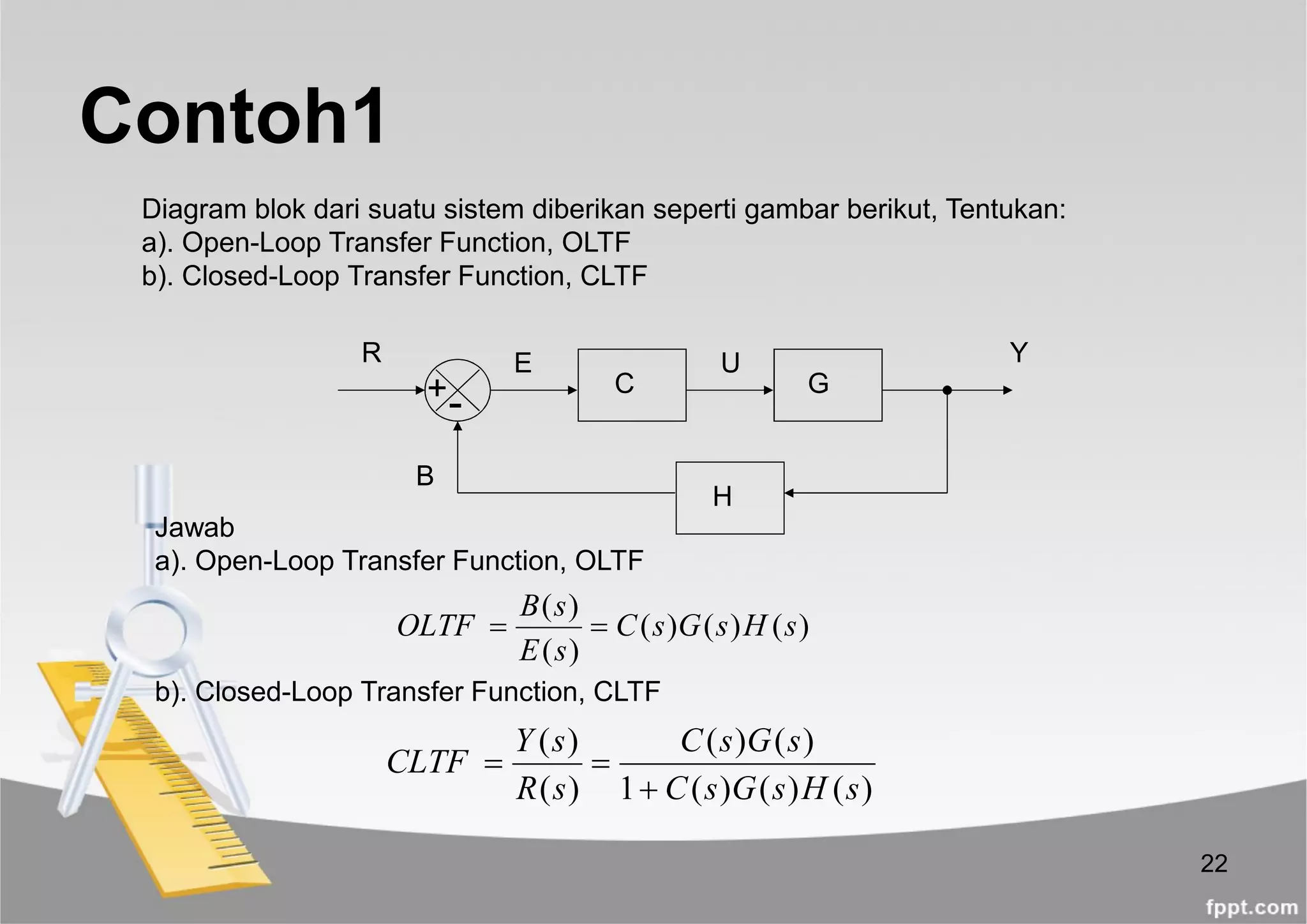
Hubungan Input Output (Lihat
Diagram Blok):
Y(s)=G(s)E(s)
E(s)=R(s)-B(s)
B(s)=H(s)Y(s)
Atau
Y(s)=G(s)[R(s)-H(s)Y(s)]
Y(s)+G(s)H(s)Y(s)=G(s)R(s)
(1+G(s)H(s))Y(s)= G(s)R(s)
Atau,](https://image.slidesharecdn.com/diagram-blok-190420153457/75/Diagram-blok-10-2048.jpg)
![12
)()()(1
)(
)(
)(
21
2
sHsGsG
sG
sD
sYD
)()()(1
)()(
)(
)(
21
21
sHsGsG
sGsG
sR
sYR
)]()()([
)()()(1
)(
)()()( 1
21
2
sDsRsG
sHsGsG
sG
sYsYsY DR
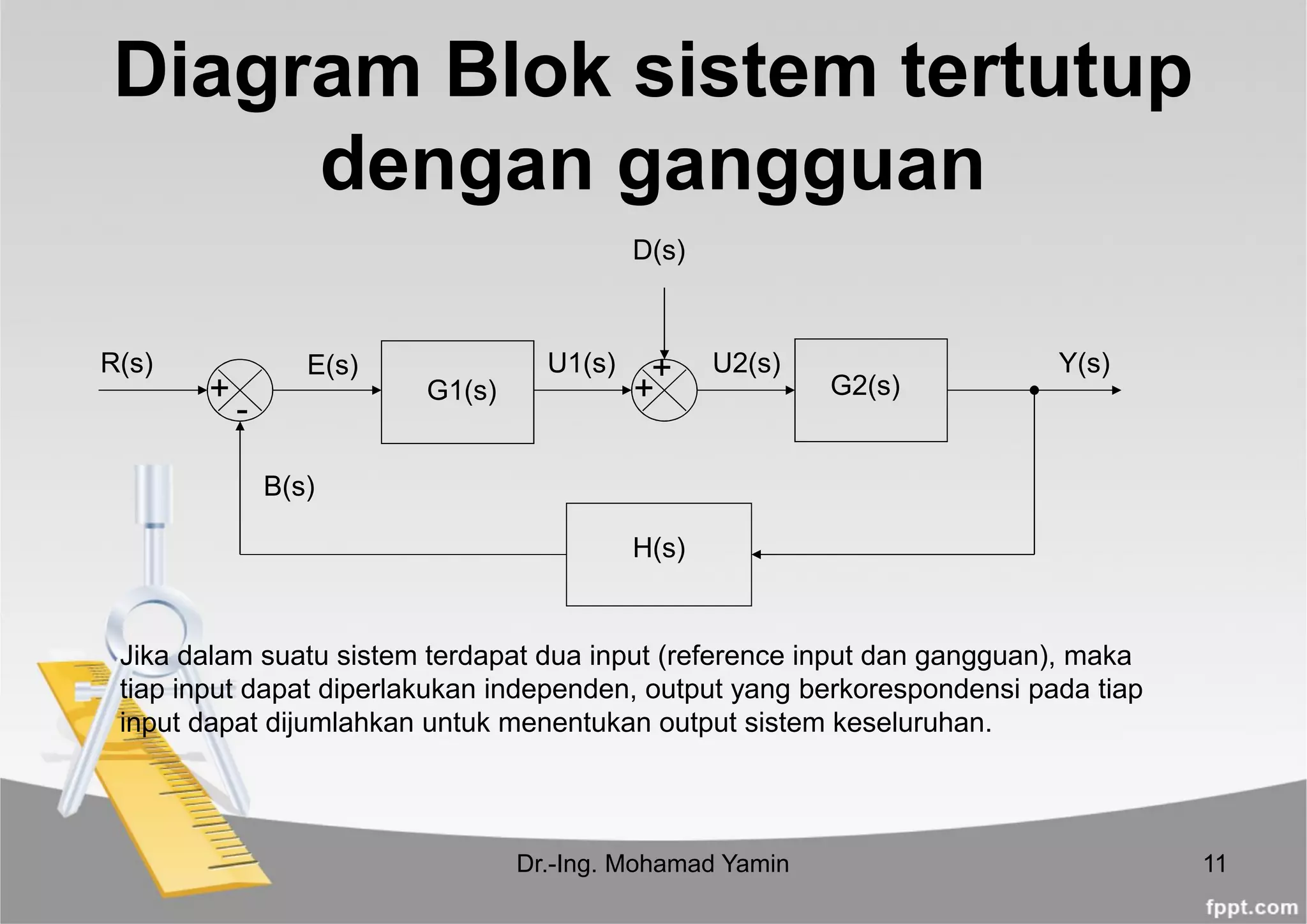
Response Y(s) terhadap gangguan D(s),
Response Y(s) terhadap referensi input R(s), dengan measumsikan gangguan
sama degan nol
Total Response Y(s),](https://image.slidesharecdn.com/diagram-blok-190420153457/75/Diagram-blok-12-2048.jpg)







![26
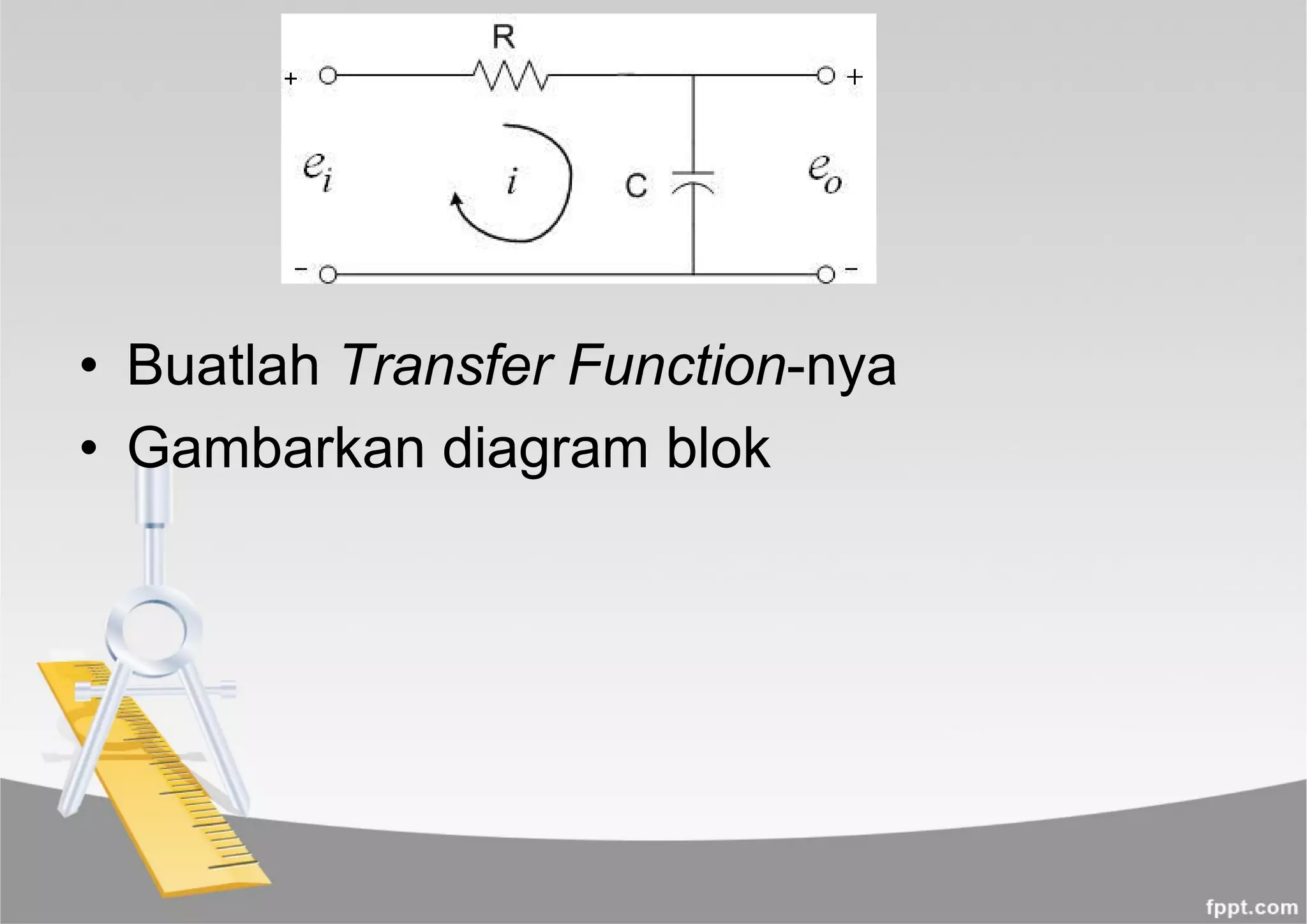
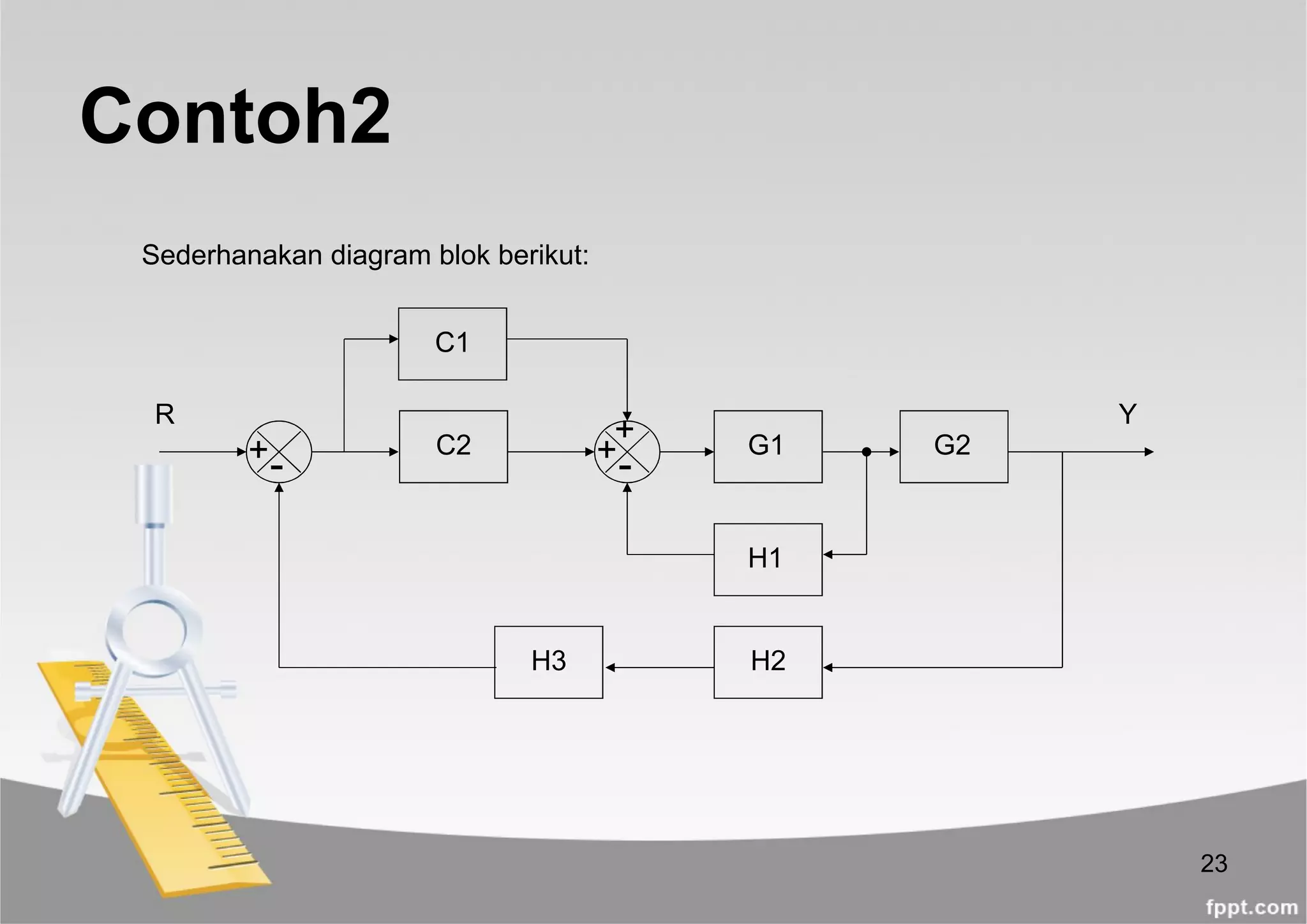
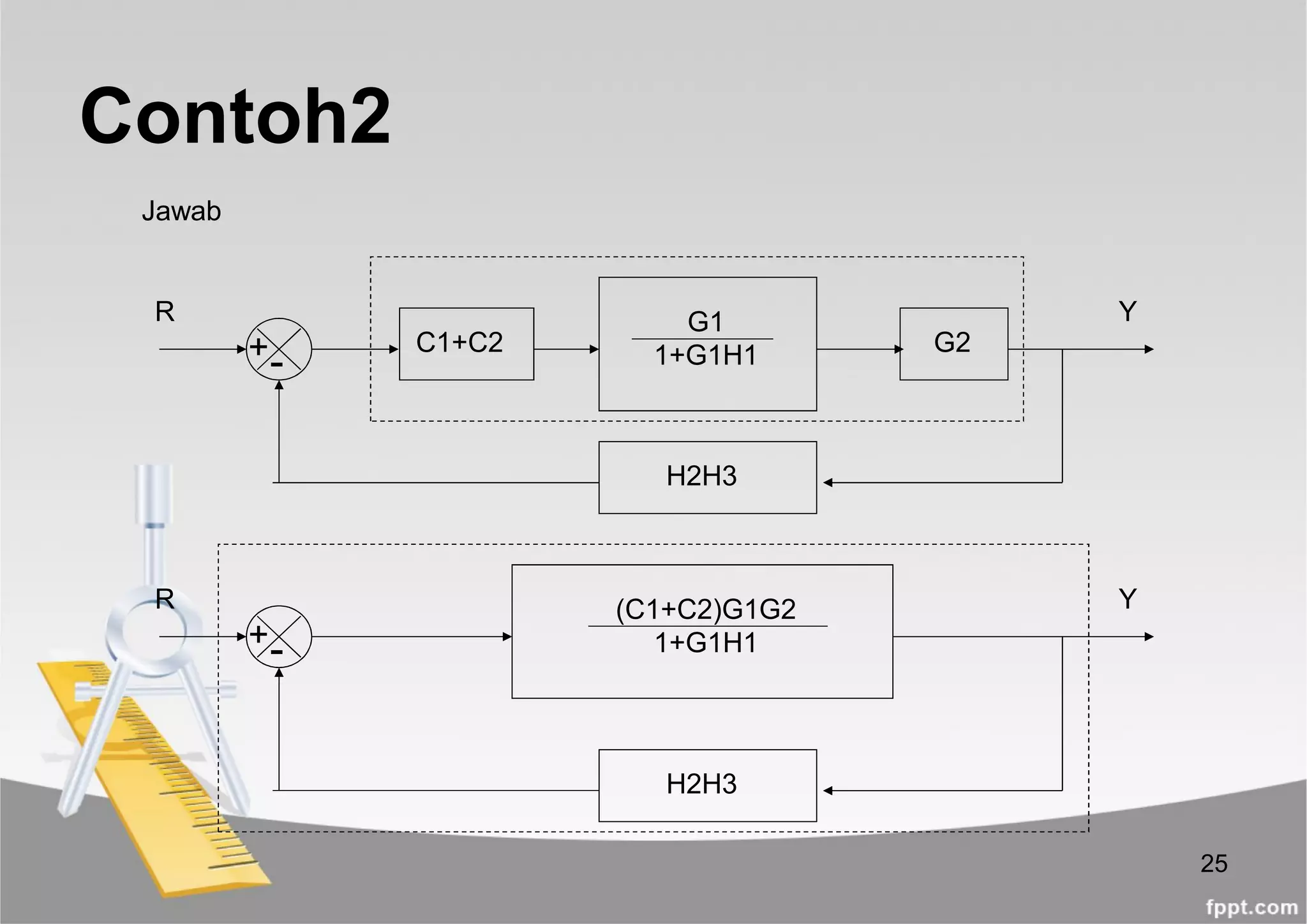
Contoh2
Diagram Blok yang disederhanakan menjadi:
YR (C1+C2)G1G2
1+G1[H1+(C1+C2)G2H2H3]](https://image.slidesharecdn.com/diagram-blok-190420153457/75/Diagram-blok-26-2048.jpg)