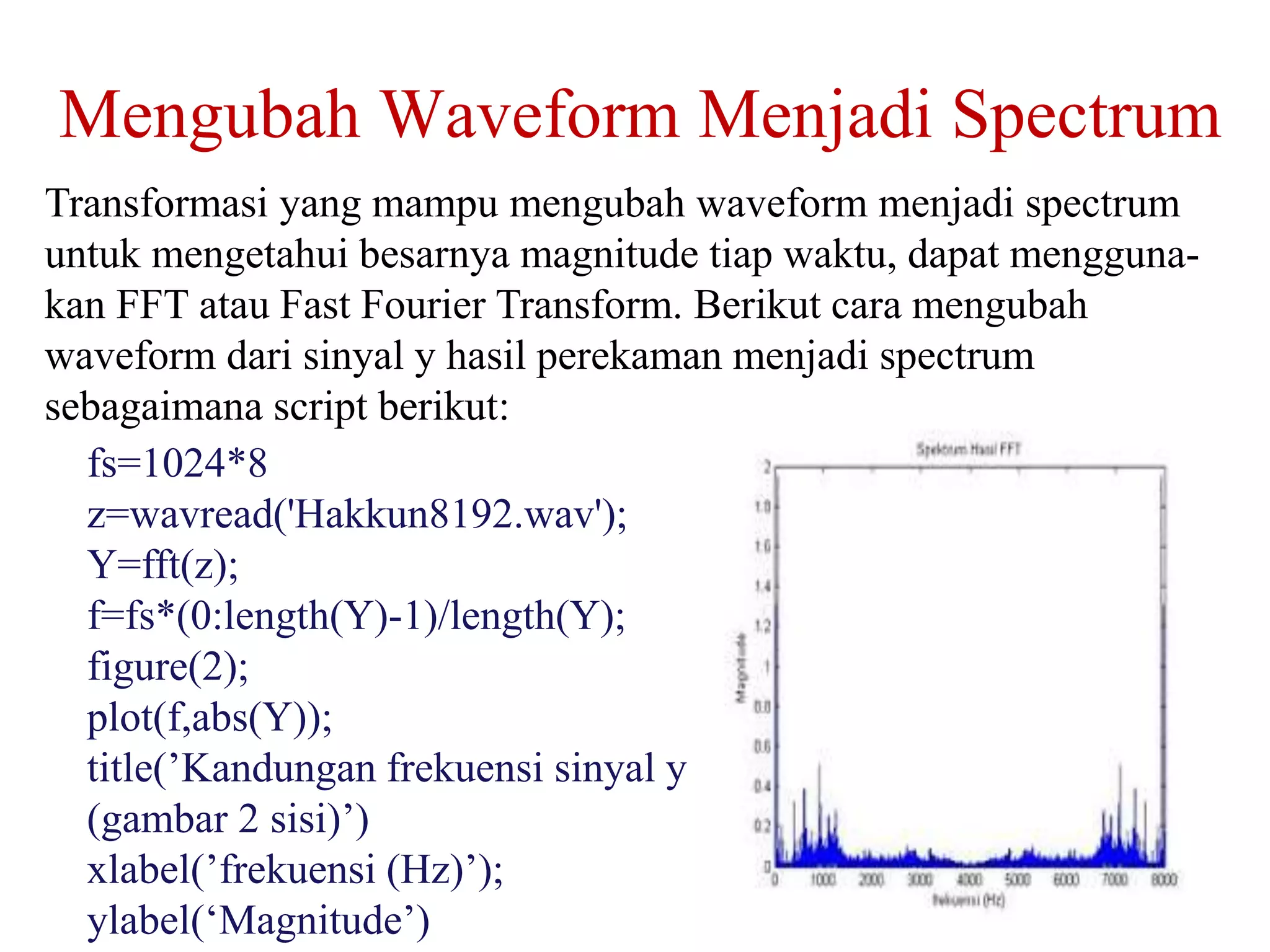
Dokumen ini adalah informasi mengenai sistem pemrosesan sinyal dalam kursus yang diajarkan oleh Dr. Hakkun Elmunsyah, termasuk jadwal, prasyarat, dan metode penilaian. Materi yang dibahas mencakup konsep dasar sinyal, analisis sistem waktu diskrit, dan berbagai jenis transformasi seperti transformasi Z dan Fourier. Selain itu, terdapat tugas kelompok dan individu untuk mendalami aplikasi komunikasi data serta sistem keamanan jaringan komputer.

1. TEUM@Sept. 2012
SISTEM PEMROSESAN SINYAL
PTE419 + PTE420

2. Informasi Umum
• Pengajar: Dr. Hakkun Elmunsyah, M.T.
• Jadual:
– Rabu: Jam ke 1 – 4 (R. G4-111 / 108)
• Prasyarat:
– MTE414, MTE412
• Bobot: 2 + 1 SKS
2

3. Komunikasi
• E-mail: hakkun@um.ac.id,
elmunsyah@yahoo.com
• Telp. : 08125206426
• Ruangan: H5.201
3

4. Penilaian
• Ujian Tengah Semester (20%)
• Ujian Akhir Semester (25%)
• Tugas kelompok dengan anggota maksimal
2 orang (25%) Matlab / Labview.
• Tugas individu (25%).
• Persentase kehadiran (5%)
4

5. Tujuan
• Memberikan pengetahuan dan keterampilan
kepada mahasiswa berkenaan konsep dan aplikasi
komunikasi data serta jaringan komputer.
• Isu penting:
– Perkembangan komunikasi data dan jaringan komputer.
– Sistem keamanan data dan evaluasi jaringan
komputer.
5

6. Materi Sistem Pemrosesan sinyal
1. Konsep dasar sinyal, sistem dan pemrosesan sinyal
1. Meliputi : Pengertian sinyal, sistem dan pemrosesan sinyal,
klasifikasi sinyal, konsep frekuensi dalam sinyal, teori
sampling, kuantisasi, pengkodean, konversi digital to analog
2. Sinyal dan sistem waktu diskrit
1. Meliputi : Klasifikasi sinyal waktu diskrit, sistem waktu
diskrit, analisa sistem LTI waktu diskrit (analisa sistem linier,
respon sistem LTI dan konvolusi)
3. Transformasi Z
1. Meliputi : Transformasi Z dan inversnya, sifat-sifat
Transformasi Z

7. Materi Sistem Pemrosesan sinyal
1. Analisa transformasi sistem LTI
Meliputi : Respons frekuensi sistem LTI, persamaan beda
2. Flow graph / Diagram Blok
Meliputi : Bentuk langsung, bentuk kaskade, bentuk paralel
3. Filter Digital
Meliputi : Design filter IIR dan FIR
4. Transformasi Fourier Diskrit (DFT)
Meliputi : Deret Fourier waktu kontinyu dan waktu diskrit, sifat-
sifat DFT, Komputasi pada DFT
5. Fast Fourier transform (FFT)
Algoritma FFT, implementasi algoritma FFT

8. References
• Kuc, Introduction to Digital Signal Processing, Mc
Graw Hill, 1982.
• Alan V. Oppenheim & R.W.Schafer, Discrete-Time
signal Processing, PHI, 1975.
• Lonnie C. Ludeman, Fundamentals of Digital Signal
Processing, Harper & Row, Publishers, Inc. 1986
• John G. Proakis & Dimitris G.M, Digital Signal
Processing third Edition, PHI, 1995.
• John G. Proakis & Dimitris G.M, Pemrosesan Sinyal
Digital – edisi bahasa Indonesia, PT Prenhalindo,
Jakarta, 1997.

9. SEJARAH PERKEMBANGAN
 Kemajuan-kemajuan pesat di bidang :
 Teknologi komputer digital
 Pabrikasi rangkaian terintegrasi
 Komputer digital + perangkat kerasnya
(30 tahun yang lalu)
 Besar dan mahal
 Aplikasi bisnis
 General purpose scientific computation
 Teknologi rangkaian terintegrasi :
 Medium-scale integration (MSI)
 Large-scale integration (LSI)
 Very-large-scale integration (VLSI)

10.  Komputer digital + perangkat kerasnya (sekarang)
 Lebih kecil, lebih cepat dan lebih murah
 Special purpose scientific computation
 Kelebihan pemrosesan sinyal digital
 Lebih presisi
 Lebih fleksibel dalam perancangan sistem
 Perangkat lunak dapat mengendalikan perangkat keras
 Operasi-operasi terprogram (algoritma)
 Kekurangan pemrosesan sinyal digital
 Untuk sinyal dengan bandwidth sangat lebar
 Real-time processing (Analog)
 Optical signal processing
 Terjadi distorsi
 Proses pencuplikan (sampling)
 Proses kuantisasi (quantization)

11. SINYAL, SISTEM DAN PEMROSESAN SINYAL
 Sinyal
 Besaran-besaran yang tergantung pada waktu dan ruang
 Besaran fisis/non fisis (variabel tak bebas)
 Waktu dan ruang (variabel bebas)
2
3
2
2
2
1
y10xy2x3)y,x(s
t20)t(s
t5)t(s



Sinyal-sinyal dengan hubungan matematis yang jelas

12. Sinyal –sinyal dengan hubungan matematis yang tidak jelas
 Suara pembicaraan (speech signals)

13.  Suatu segmen dari suara pembicaraan dapat
direpresentasikan sebagai :
 Sejumlah sinyal sinusoidal dengan amplituda,
frekuensi dan fasa yang berbeda
)]t(t)t(F2[sin)t(A)t(s ii
N
1i
i  
 Informasi yang terkandung di dalam suatu sinyal
ditentukan dengan mengukur :
 Amplituda(A)
 Frekuensi(F)
 Fasa()

14.  Sinyal electrocardiogram (ECG)
 Sinyal elektronik yang berasal dari aktivitas jantung
 Informasi mengenai kondisi dari jantung pasien
 Sinyal electroencephalogram (EEG)
 Sinyal elektronik yang berasal dar aktivitas otak
 Sinyal-sinyal , ,  dan 
 Sinyal-sinyal dengan satu variabel bebas (waktu)
 Suara pembicaraan, ECG dan EEG
 Sinyal dengan dua variabel bebas (ruang)
 Gambar (image signal)

15.  Sistem
 Alat fisik yang melakukan suatu operasi pada suatu sinyal
 Filter
 Mereduksi (mengurangi) derau (noise)
 Alat non fisik
 Software (perangkat lunak)
 Melakukan sejumlah operasi-operasi matematik
 Algoritma
 Pemrosesan sinyal (Signal processing)
 Operasi-operasi yang dilakukan pada suatu sinyal

16. ELEMEN-ELEMEN DASAR DARI Pemrosesan Sinyal
 Sistem pemrosesan sinyal analog
Sinyal
input
analog
Pemroses
sinyal
analog
Sinyal
output
analog
Sinyal
input
analog
Pemroses
sinyal
digital
 Sistem pemrosesan sinyal digital
A/D
Converter
Sinyal
output
analog
D/A
Converter
Sinyal input digital Sinyal output digital

17. KLASIFIKASI SINYAL
 Single-channel signal
 Hanya terdiri dari satu sinyal (variabel tak bebas)
 Nilainya bisa real atau kompleks
)t3sin(jA)t3cos(AAe)t(s
)t3sin(A)t(s
t3j
2
1



 Multi-channel signal
 Lebih dari satu sinyal (variabel tak bebas)
 Gelombang gempa (3 channels)
 ECG (3 channels/12 channels)

18. Gelombang gempa :
 Primary wave (Longitudinal)
 Secondary wave (Transversal)
 Surface wave (Permukaan)











)t(S
)t(S
)t(S
)t(S
3
2
1
Vektor

19.  Sinyal satu dimensi
 Hanya fungsi dari satu variabel bebas
 Multi-dimensional signal
 Fungsi lebih dari satu variabel bebas
)y,x(IS 
Sinyal dua
dimensi

20.  Sinyal tiga dimensi
 Gambar televisi hitam-putih
)t,y,x(IS 
 Multichannel multidimensional signal
 Gambar televisi berwarna











)t,y,x(I
)t,y,x(I
)t,y,x(I
)t,y,x(I
b
g
r

21.  Sinyal waktu kontinu
 Speech signal
 Sinyal waktu diskrit
 Hanya ada pada waktu-waktu tertentu saja


 

lainnya0
0n8,0
)n(x
n
0,8
0,64

22.  Sinyal berharga kontinu (Continuous-valued signal)
 Dapat berharga berapa saja
Sinyal berharga kontinu dan waktu diskrit

23.  Sinyal berharga diskrit (Discrete-valued signal)
 Berharga pada beberapa kemungkinan saja
 Sinyal digital
 Waktu diskrit
 Harga diskrit

24.  Sinyal deterministik
 Harganya dapat diprediksi
 Sinyal acak (random signal)
 Harganya tidak dapat diprediksi

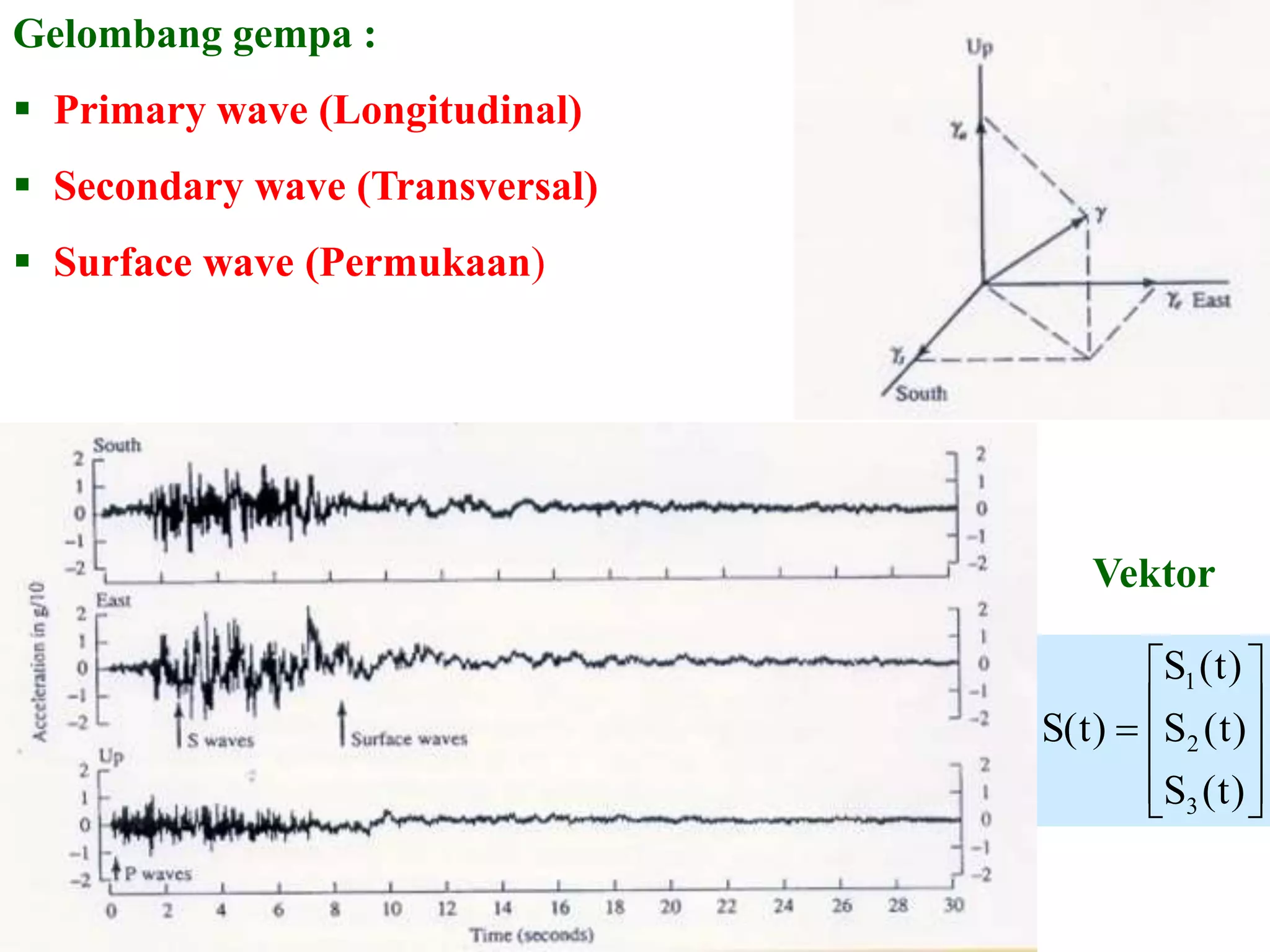
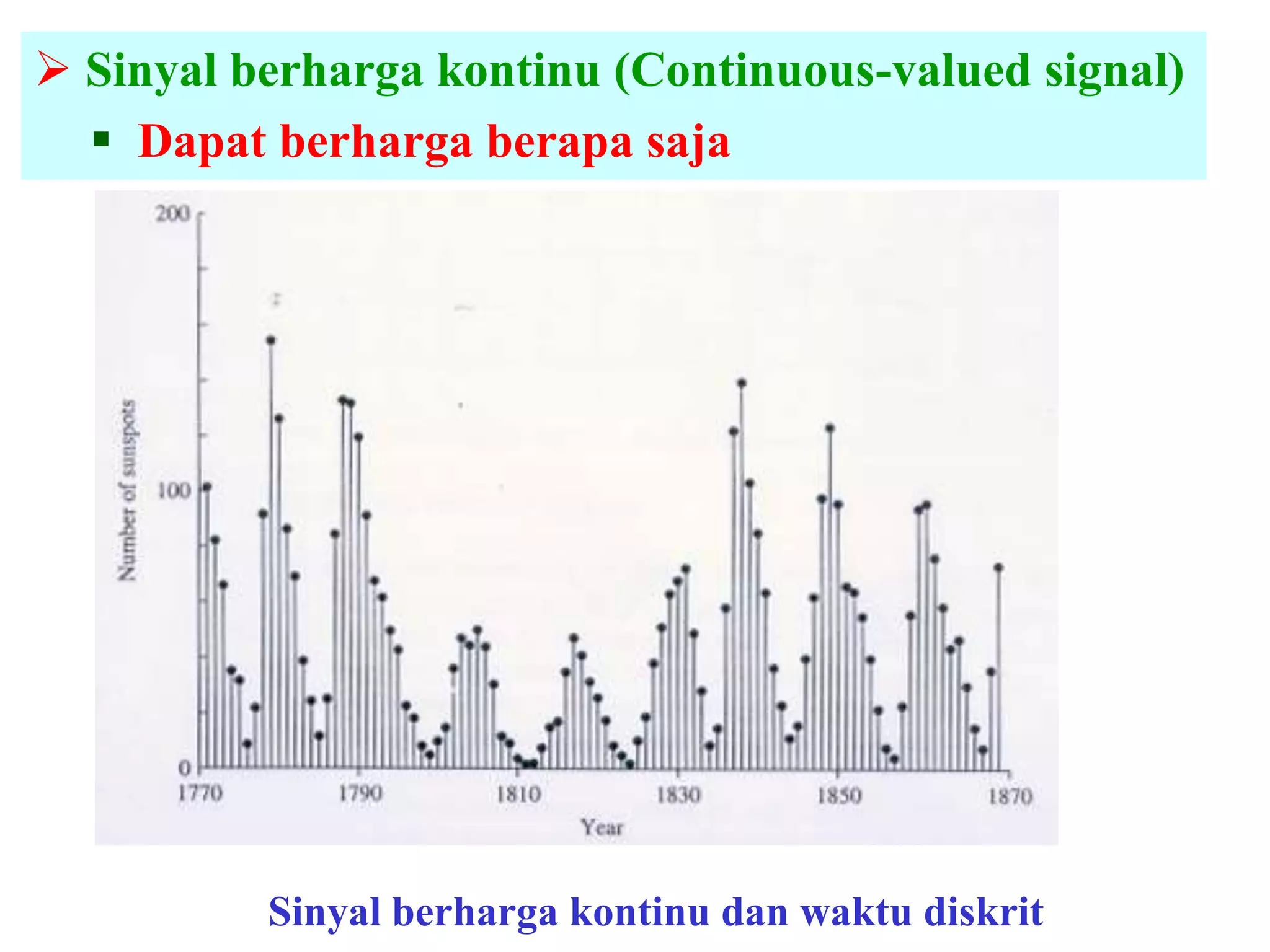
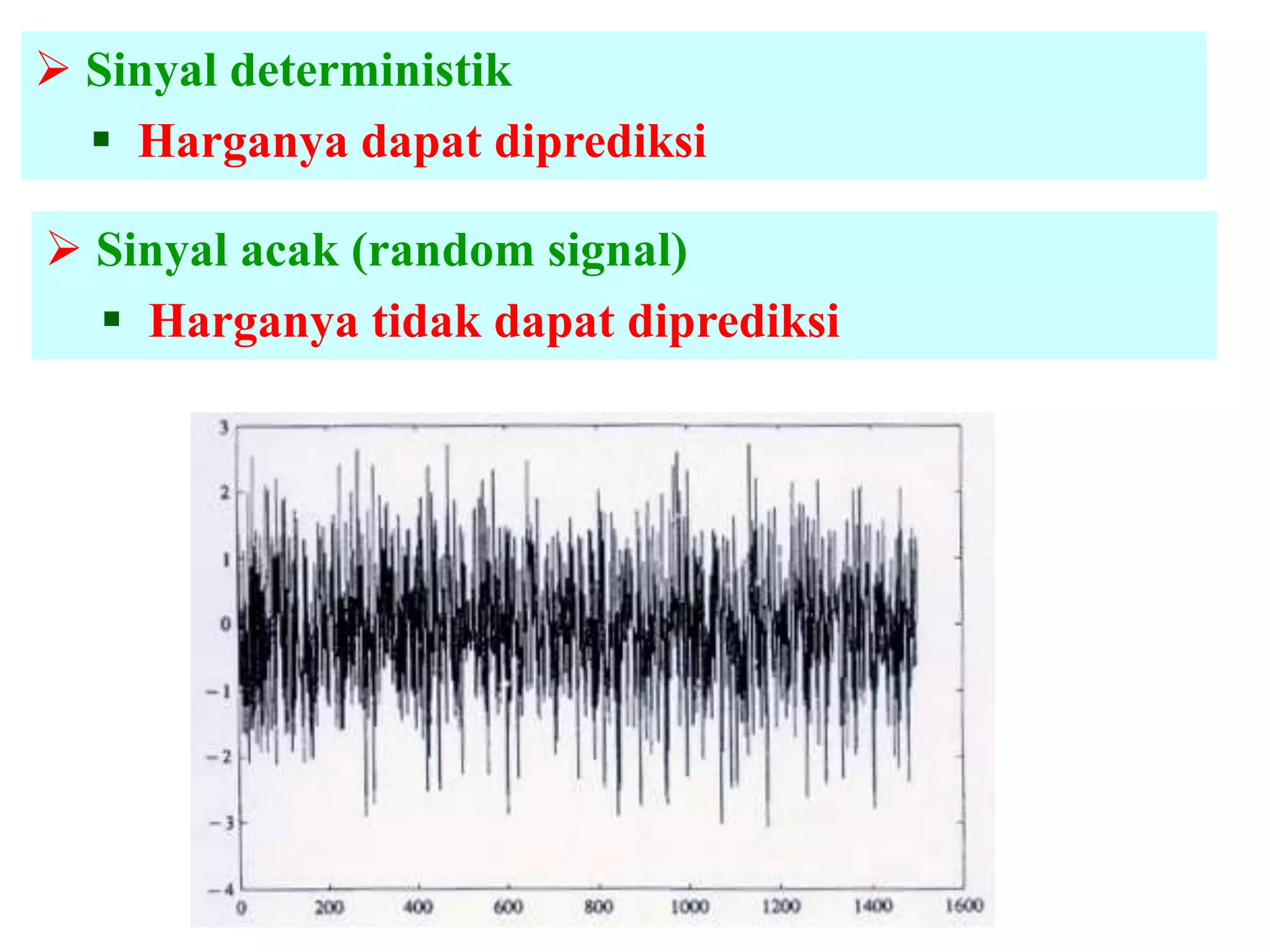
26. KONSEP FREKUENSI
 Sinyal sinusoidal waktu kontinu
 t)tcos(A)t(xa
F = frekuensi [siklus/detik, hertz (Hz)]
t = waktu
A = amplituda
 = frekuensi sudut[radian/detik]
 = fasa [radian]
)tF2cos(A)t(xF2 a 

27. )tcos(A)t(xa 
 Untuk setiap frekuensi F  xa(t) periodik
dasarperioda
F
1
T)t(x)Tt(x papa 
 Sinyal-sinyal sinusoidal waktu kontinu dengan frekuensi
berbeda dapat dibedakan
 Frekuensi diperbesar
Untuk suatu waktu tertentu jumlah perioda bertambah

28.  Sinyal sinusoidal waktu diskrit
 n)ncos(A)n(x
f = frekuensi [siklus/sampel]
n = bilangan bulat (integer)
A = amplituda
 = frekuensi [radian/sampel]
 = fasa [radian]
)nf2cos(A)n(xf2 

29. )nf2cos(A)n(x o 
 x (n) periodik hanya bila frekuensi f merupakan
bilangan rasional
)nf2cos(]Nf2nf2cos[])Nn(f2cos[
)n(x)Nn(x
oooo 

12
1
f
6
oo 


3


N
k
fk2Nf2 oo 
Harga terkecil dari N disebut perioda dasar

30.  Sinyal-sinyal sinusoidal waktu diskrit dengan frekuensi-
frekuensi yang berbeda sebanyak 2 k adalah identik
(tidak dapat dibedakan)
)ncos(]n2ncos[]n)2cos[( ooo 
k2
2,1,0k)ncos(A)n(x
ok
kk

 
2
1
f
2
1

 Frekuensi diperbesar  harga maksimum f = 1/2

31. )ncos()n(x o

32.  2)ncos()n(x
o222
o111
2)ncos(A)n(x
)ncos(A)n(x


)n(x)ncos(A
)ncos(A)nn2cos(A
n)2cos(A)ncos(A)n(x
1o
oo
o22



2 adalah alias dari 1

33.  Sampling (pencuplikan)
 Quantization (kuantisasi)
 Coding (pengkodean)
ANALOG TO DIGITAL CONVERSION
01011
Xa(t)
QuantizerSampler Coder
Discrete-time signal
Quantized signal
X(n) Xq(n)
Digital signal
Analog signal

34.  Sampling (pencuplikan)
 Sinyal waktu kontinu  sinyal waktu diskrit
 T = sampling interval
 Fs = sampling rate (sampel/detik)

35. TRANSFORMASI VARIABEL BEBAS PADA
PEMROSESAN SINYAL
• Pergeseran
 x(t-t0) → x(t) yg digeser sebesar t0
 t0 > 0 → sinyal didelay sebesar t0
 t0 < 0 → sinyal diforward sebesar t0
• Pencerminan
 x(-t) → sinyal x(t) yang direfleksikan thdp t=0
• Gabungan Pergeseran&Pencerminan
– X(3-t) = x(-t+3)=x(-(t-3))
• X(t) direfleksikan thd t=0 kemudian digeser kekanan 3 satuan.
– X(-t-3) = x(-(t+3))
• X(t) direfleksikan thd t=0 kemudian digeser kekiri 3 satuan
• Penskalaan Waktu → x()
– || > 1 → x(t) menyatakan x(t) yg disusutkn interval waktunya
– || < 1 → x(t) menyatakan x(t) yg dikembangkn interval waktunya

36. Time Shifting &Time Scaling
Pergeseran
Penskalaan waktu

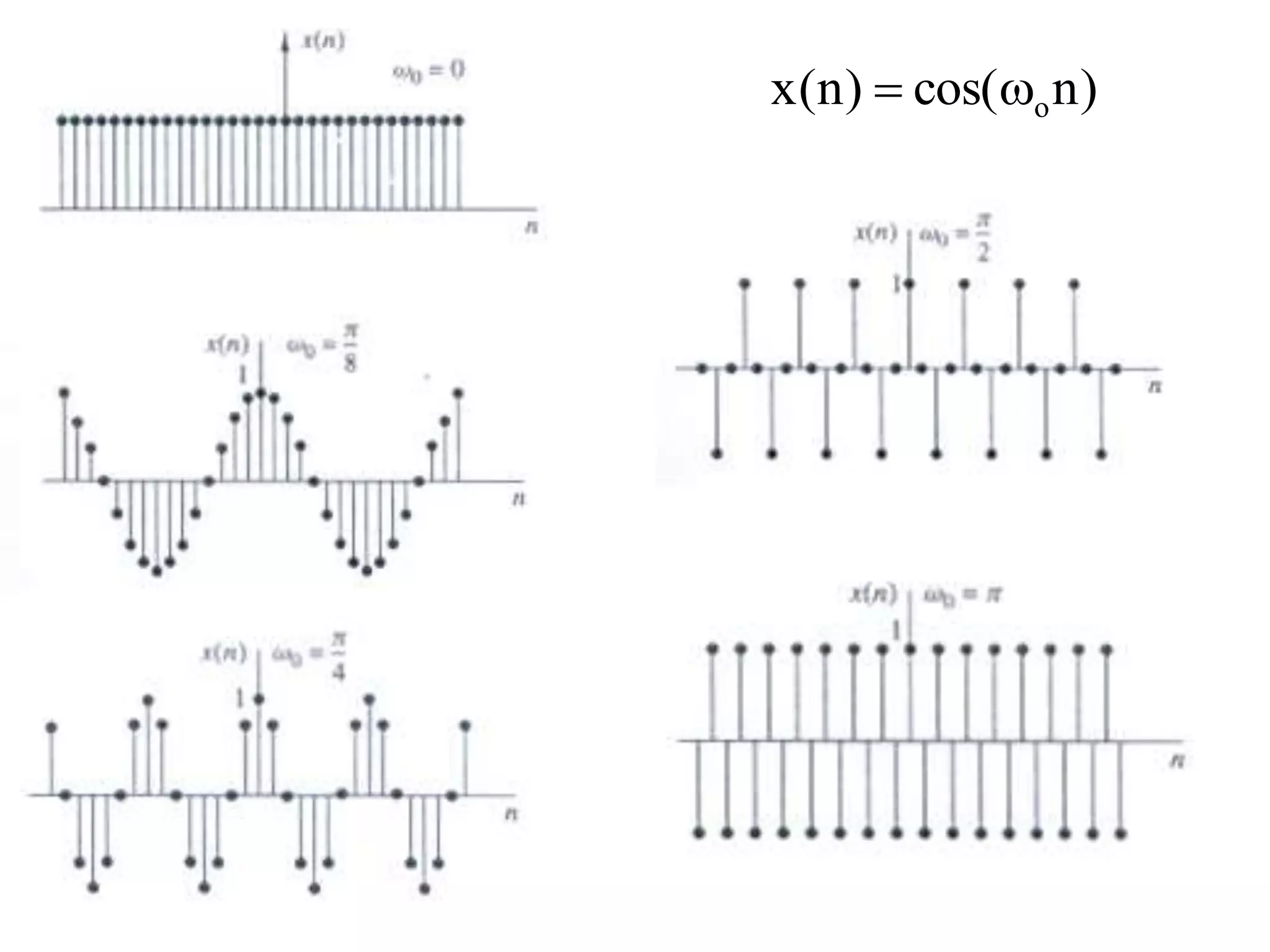
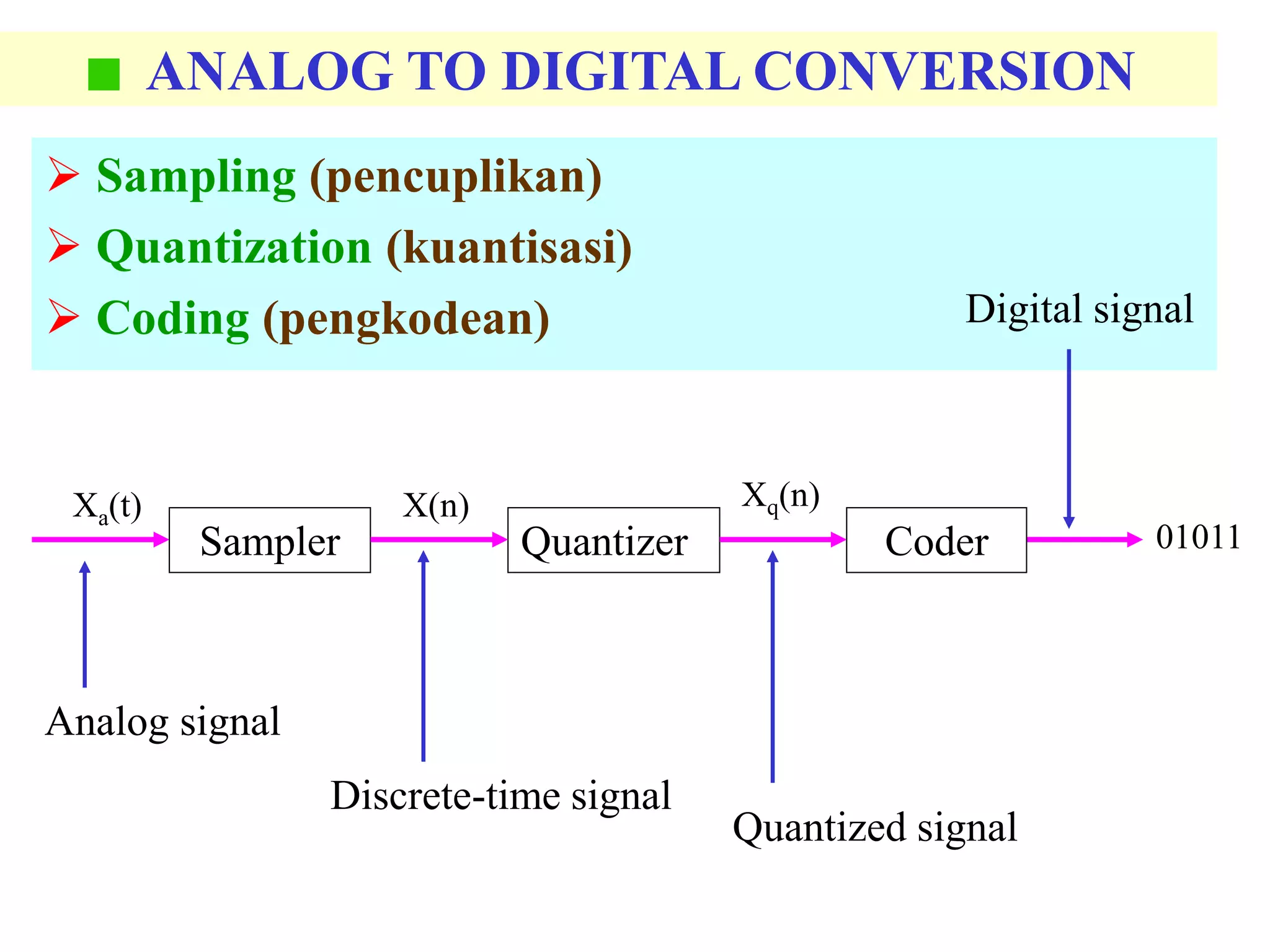
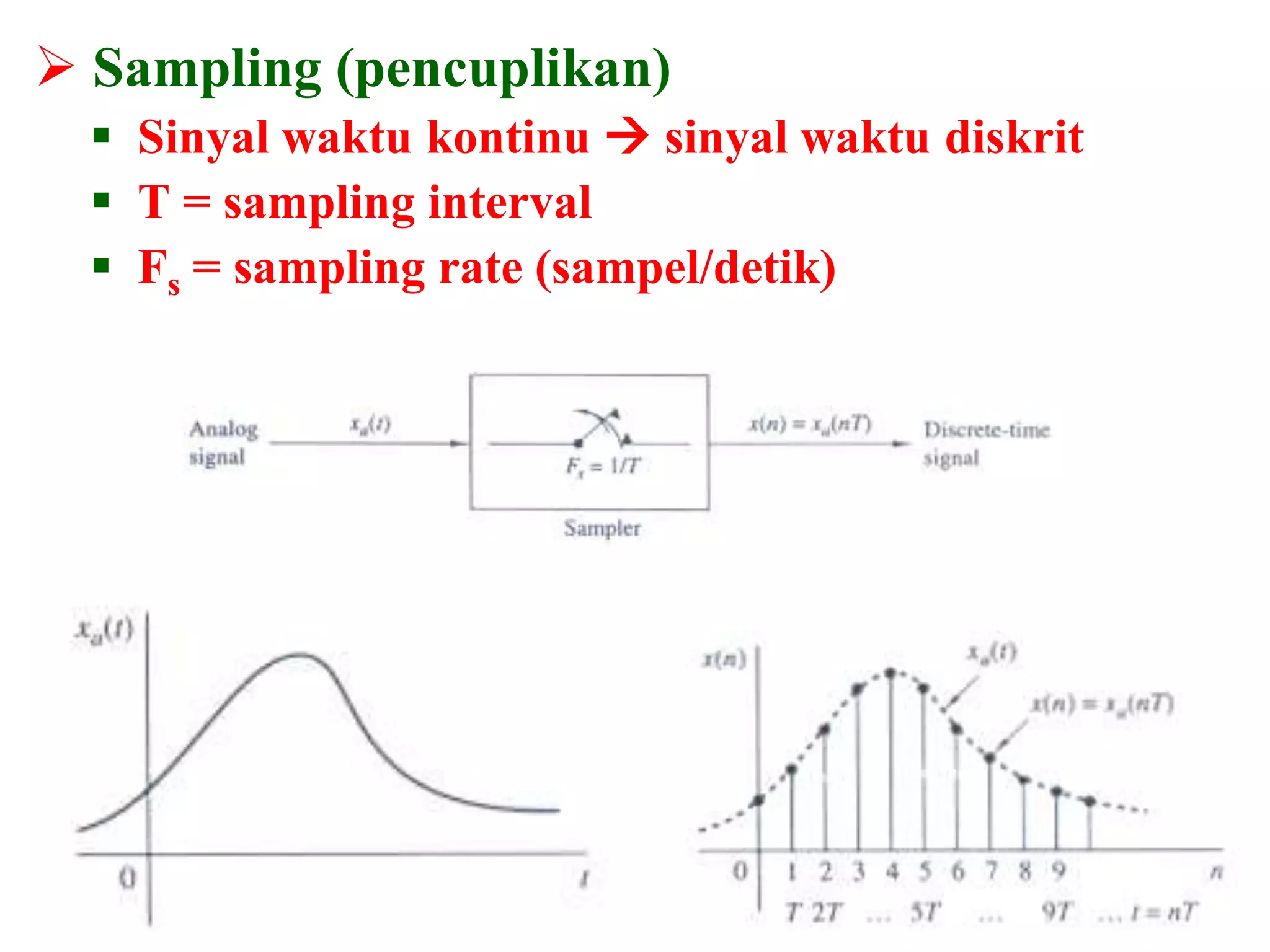
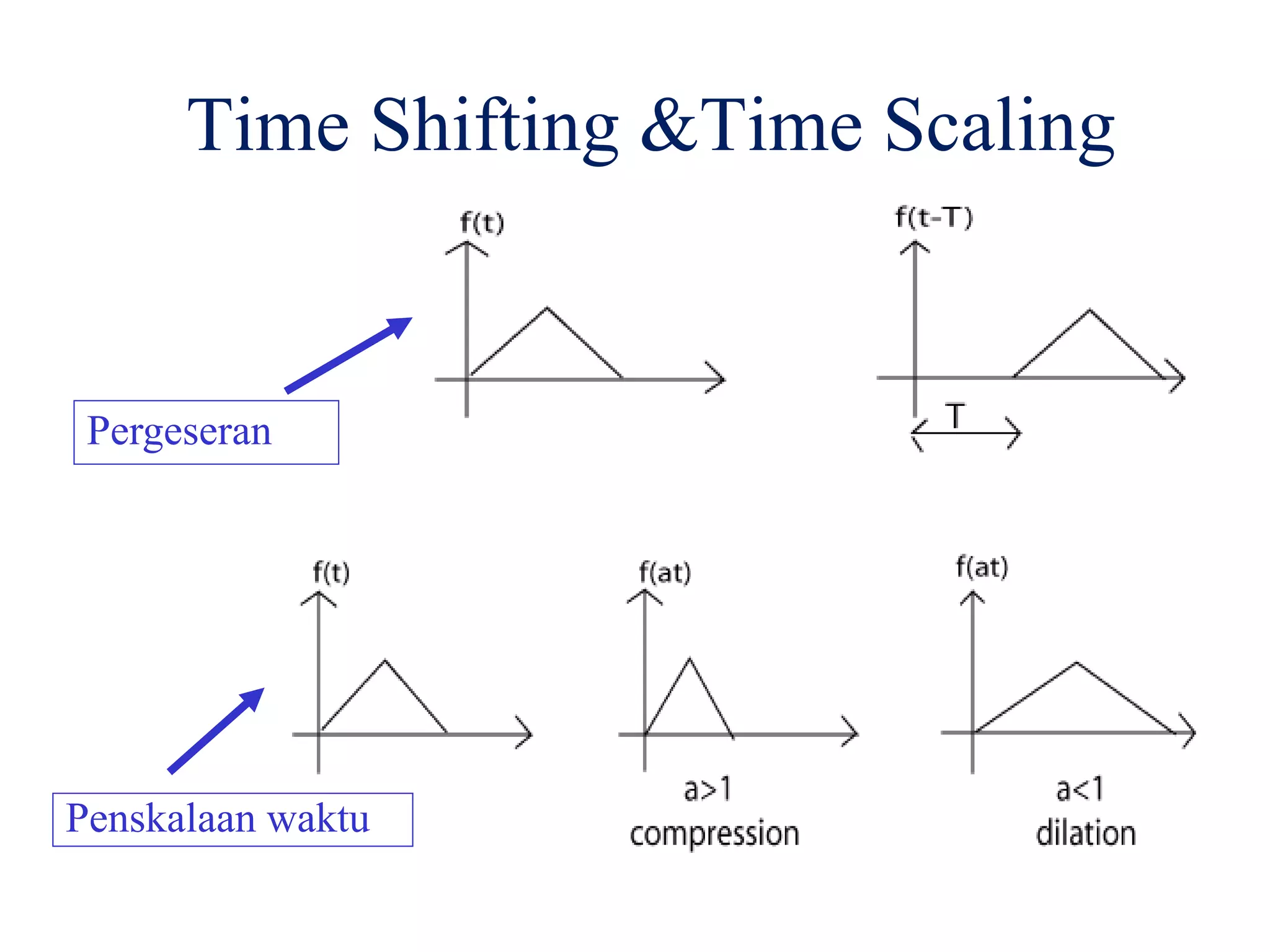
37. • Sinyal wAktu Kontinyu Elementer
– Fungsi Unit Step, u(t)=1 utk t>0, u(t) = 0 utk t<0
– Fungsi Ramp Satuan, r(t)=0 utk t<0, r(t)=t utk t>0
– Fungsi Impulse Satuan, (t)=1 utk t=0, (t)=0 utk t lain
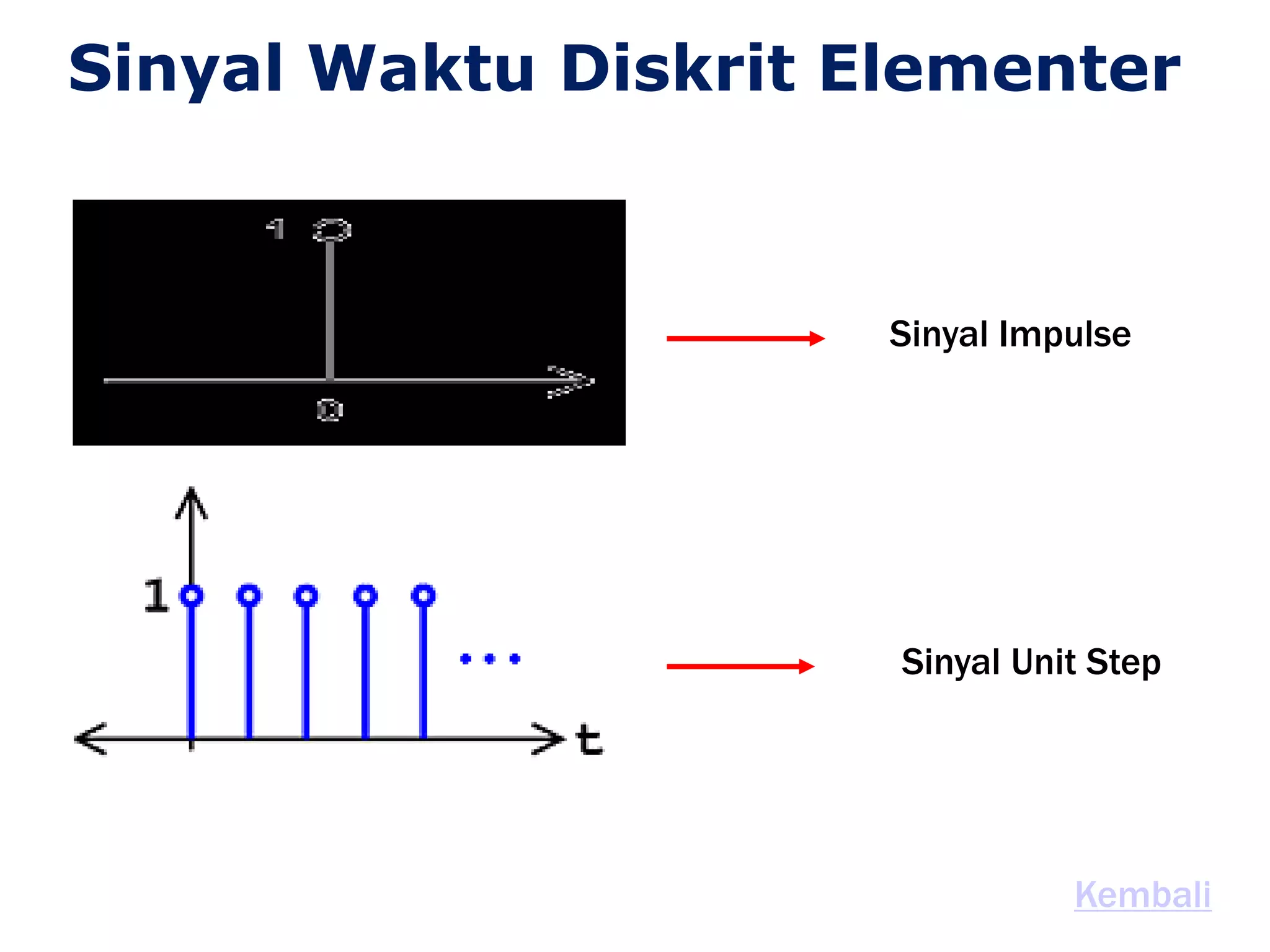
• Sinyal Waktu Diskrit Elementer
– Fungsi Unit Step dan Impulse
• u[n]=1 utk n>0, u[n] = 0 utk n<0
• [n]=1 utk n=0, [n]=0 utk n lain
– Sekuen Eksponensial x[n]=C.e(j.o.n), x[n]=x(n+N)
• o.N = m.2∏ → o/2∏ = m/N
– X[n] akan periodik hanya jika o/2∏ berupa bil rasional
Sinyal-Sinyal Elementer (Dasar)

38. Sinyal Waktu Kontinyu Elementer
Sinyal Unit Step
Sinyal Ramp Satuan
Kembali
Sinyal Impulse

39. Sinyal Waktu Diskrit Elementer
Sinyal Impulse
Sinyal Unit Step
Kembali

40. Latihan Olah Sinyal

41. Penguatan dan Pelemahan Sinyal

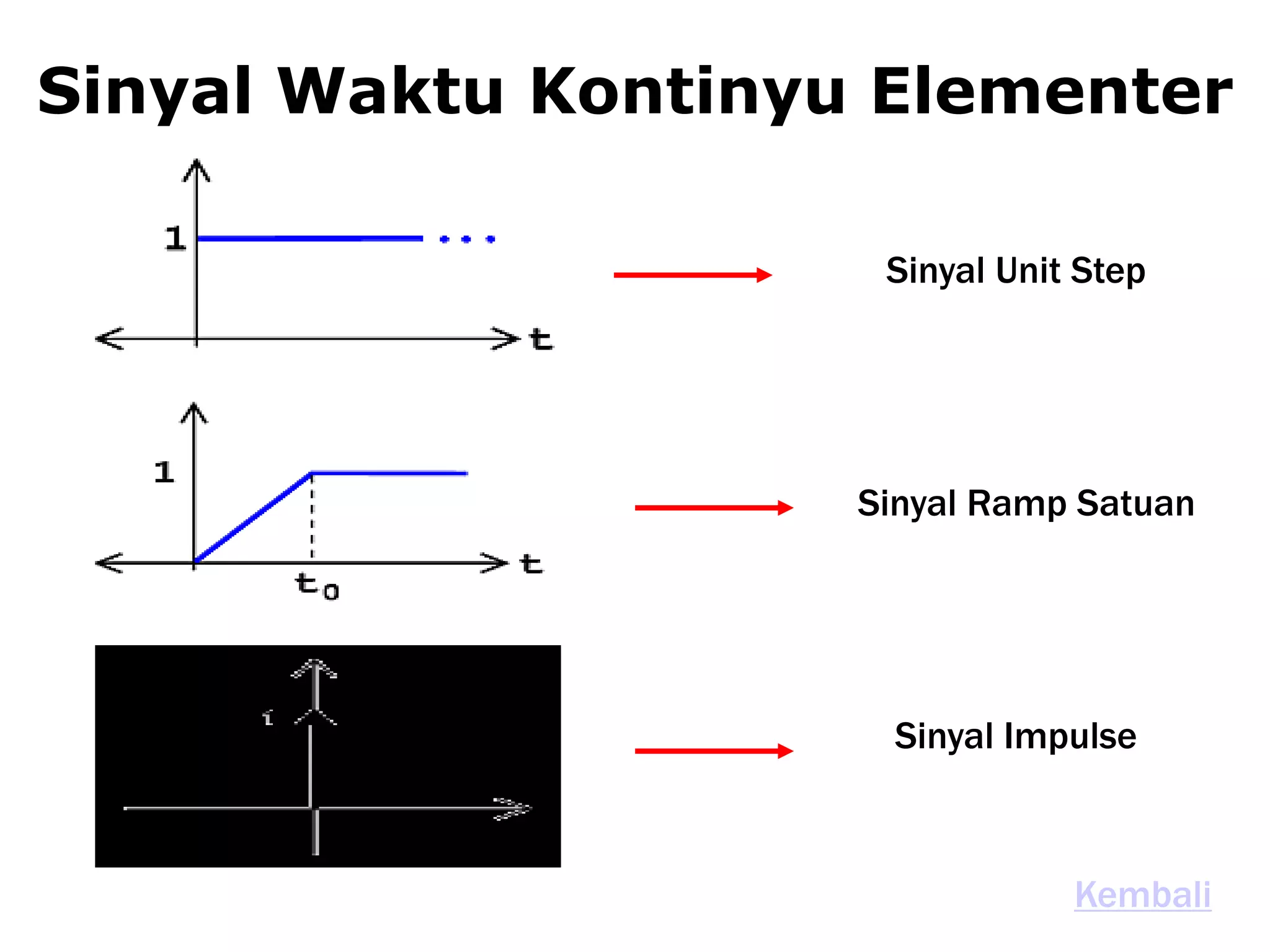
42. Manipulasi Sinyal Diskrit
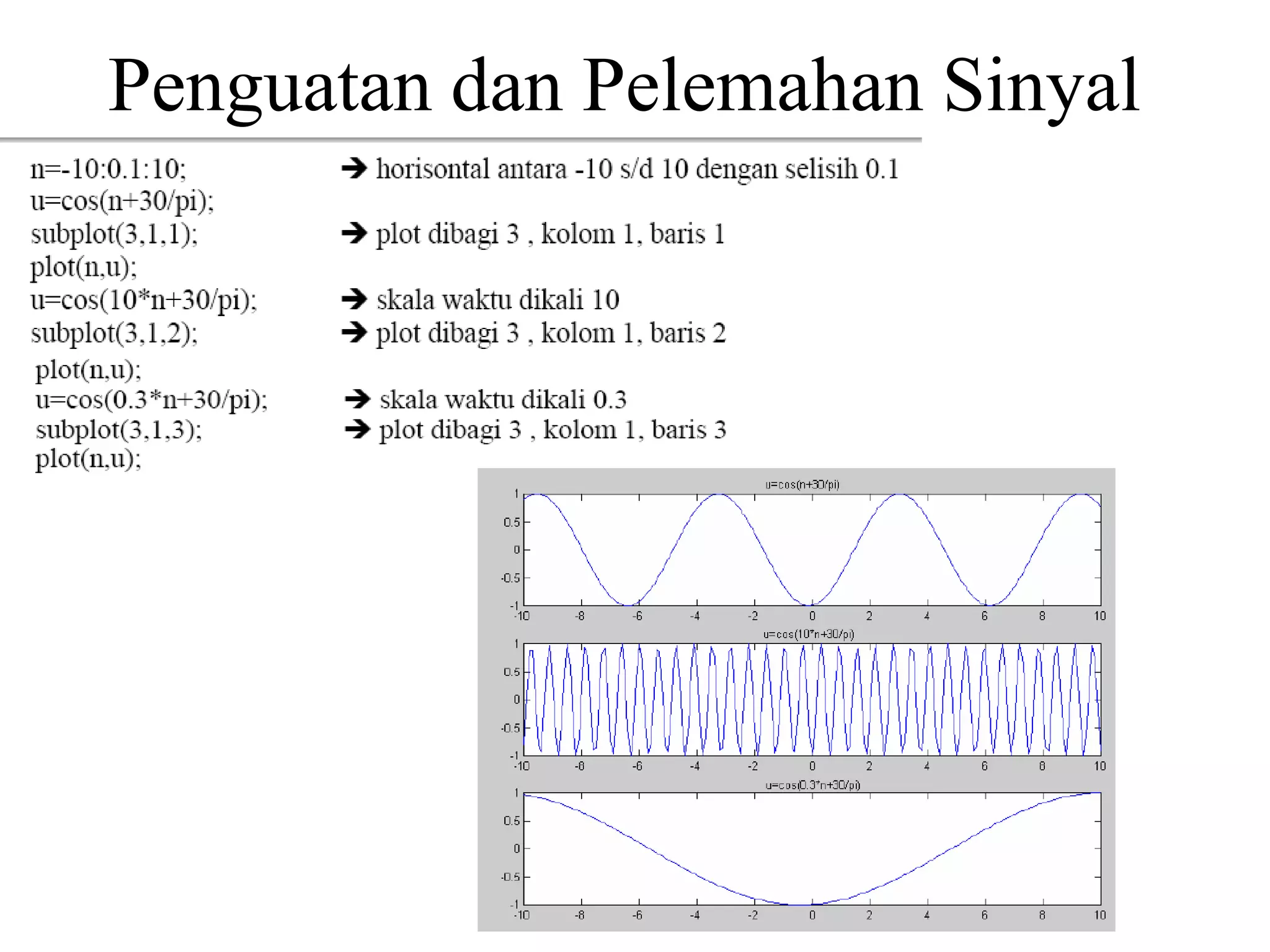
n = -10:10;
x = [zeros(1,10) 1 4 -2 0 -1 2 zeros(1,5)]; title('Sinyal x(n)');
stem(n,x)

43. %x(n) yang digeser satu kekiri
n = -10:10;
n1 = n+1;
n2 = -n+1;
x = [zeros(1,10) 1 4 -2 0 -1 2 zeros(1,5)];
subplot (2,1,1); stem(n,x);
axis([-10 10 -2 4]); title('Sinyal x(n)');
subplot (2,1,2); stem(n1,x);
axis([-10 10 -2 4]); title('Sinyal x(n-1)');
Manipulasi Sinyal Pergeseran

44. Pencerminan Sinyal dan Pergeseran
%Penceminan x(n) dan digeser satu kekiri
n = -10:10;
n1 = n+1;
n2 = -n+1;
x = [zeros(1,10) 1 4 -2 0 -1 2 zeros(1,5)];
subplot (2,1,1); stem(n,x);
axis([-10 10 -2 4]); title('Sinyal x(n)');
subplot (2,1,2); stem(n2,x);
axis([-10 10 -2 4]); title('Sinyal x(-n+1)');

45. Tugas kelompok
di kumpulkan hari ini via elmunsyah@gmail.com
12 September 2012
1. Jelaskan perbedaan sinyal analog dan sinyal digital. Beri contoh
pada bidang komunikasi data komputer
2. Buat script matlab dan gambarnya, manipulasi sinyal sebagai
berikut:
Sinyal = -8 -7 -6 -5 -4 -3 -2- 1 0 1 2 3 4 5 6 7 8
Selanjutnya cerminkan sinyal tersebut, kemudian geser 3 step kekanan

46. Materi 19 September 2012
1. Aritmatika Sinyal (Penguatan, Pelemahan,
Penjumlahan, Pengurangan dan perkalian)
2. Aplikasi Pengolahan Sinyal

47. Aritmatika Sinyal

48. Pengolahan Sinyal

49. Penguatan dan Pelemahan Sinyal

50. Listing
Penjumlahan Sinyal
1.
2.

51. Listing
Perkalian Sinyal
1.
2.

52. Buatlah Simulasi Aplikasi Pengolahan Sinyal
Rangkaian-1 Berikut
Catatan:
1. Perhatikan nilai Resistor
2. Tampilkan Sinyal Analog:
V4, V3, Vo dan Vo Diskrit
V4
V3
Vo

53. Buatlah Simulasi Aplikasi Pengolahan Sinyal
Rangkaian-2 Berikut
Catatan:
1. Perhatikan nilai Resistor
2. Tampilkan Sinyal Analog:
V4, V3, Vo dan Vo Diskrit
2K
Vo

54. Tugas Perorangan
di kumpulkan hari ini via elmunsyah@gmail.com
1. Kembangkan script matlab latihan penjumlahan dan perkalian,
dengan menambah tampilan sinyal diskrit y3 pada tampilan matrik
gambar 4x4. (2 Blok Gambar)
2. Jawablah pertanyaan pada masing-masing point 1 diatas. (fa=4&/8;
pha2=0,25*pi dan 1,5*pi). (4 Blok Gambar)
3. Buat script matlab dan gambarnya, simulasi aplikasi pengolahan
sinyal pada rangkaian pertama dan kedua. (2 Blok Gambar)

55. Materi 3 Oktober 2012

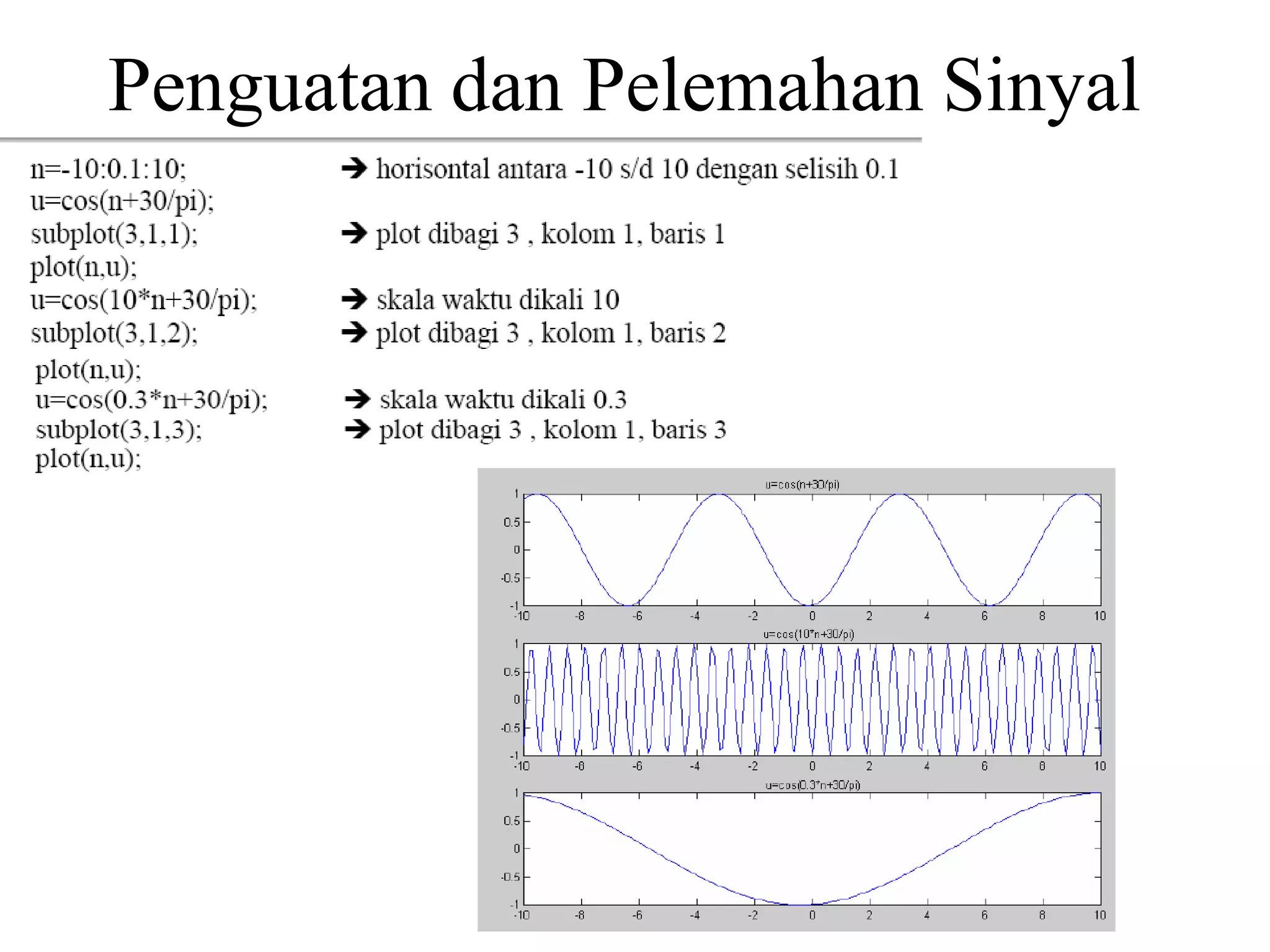
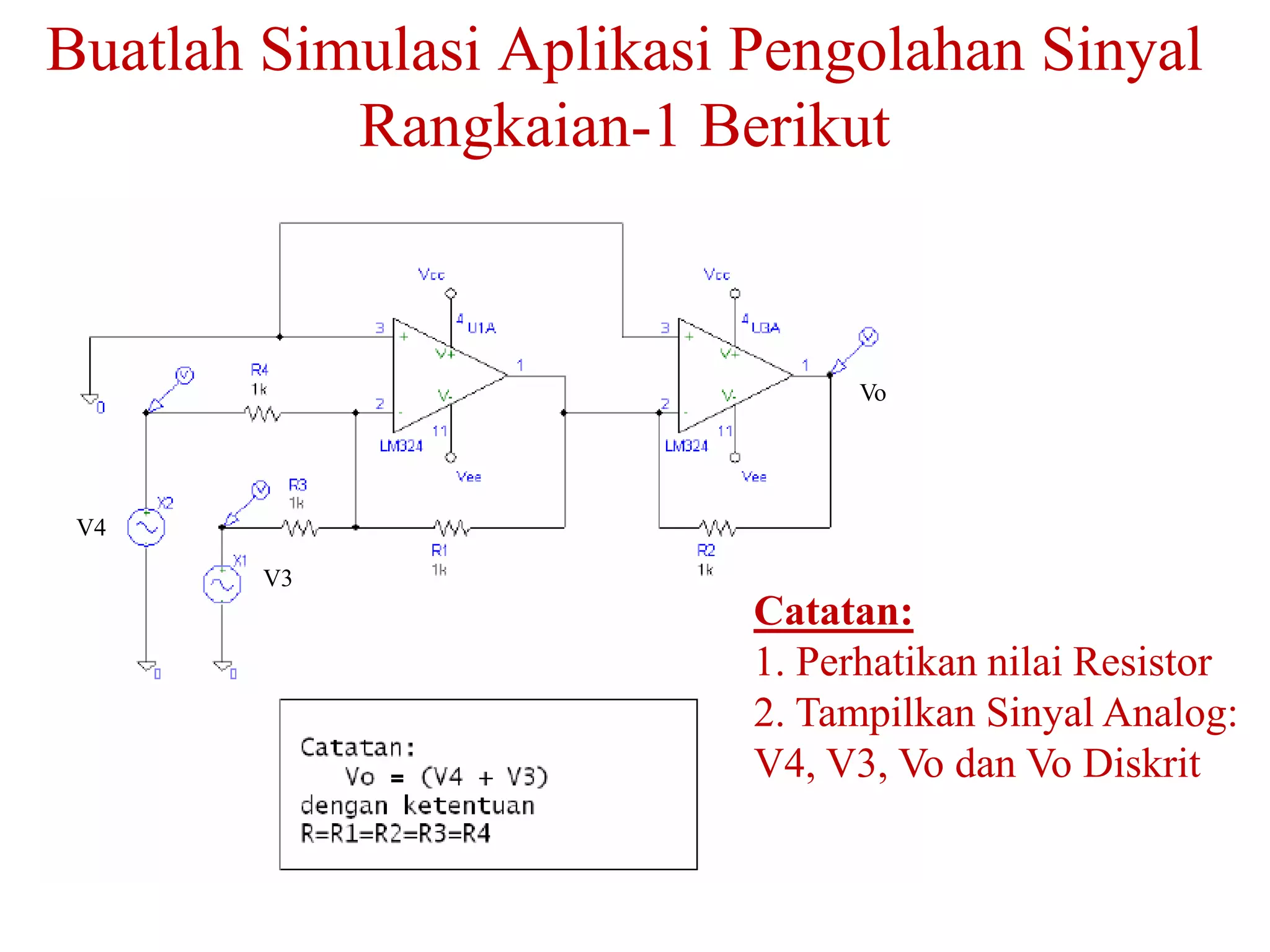
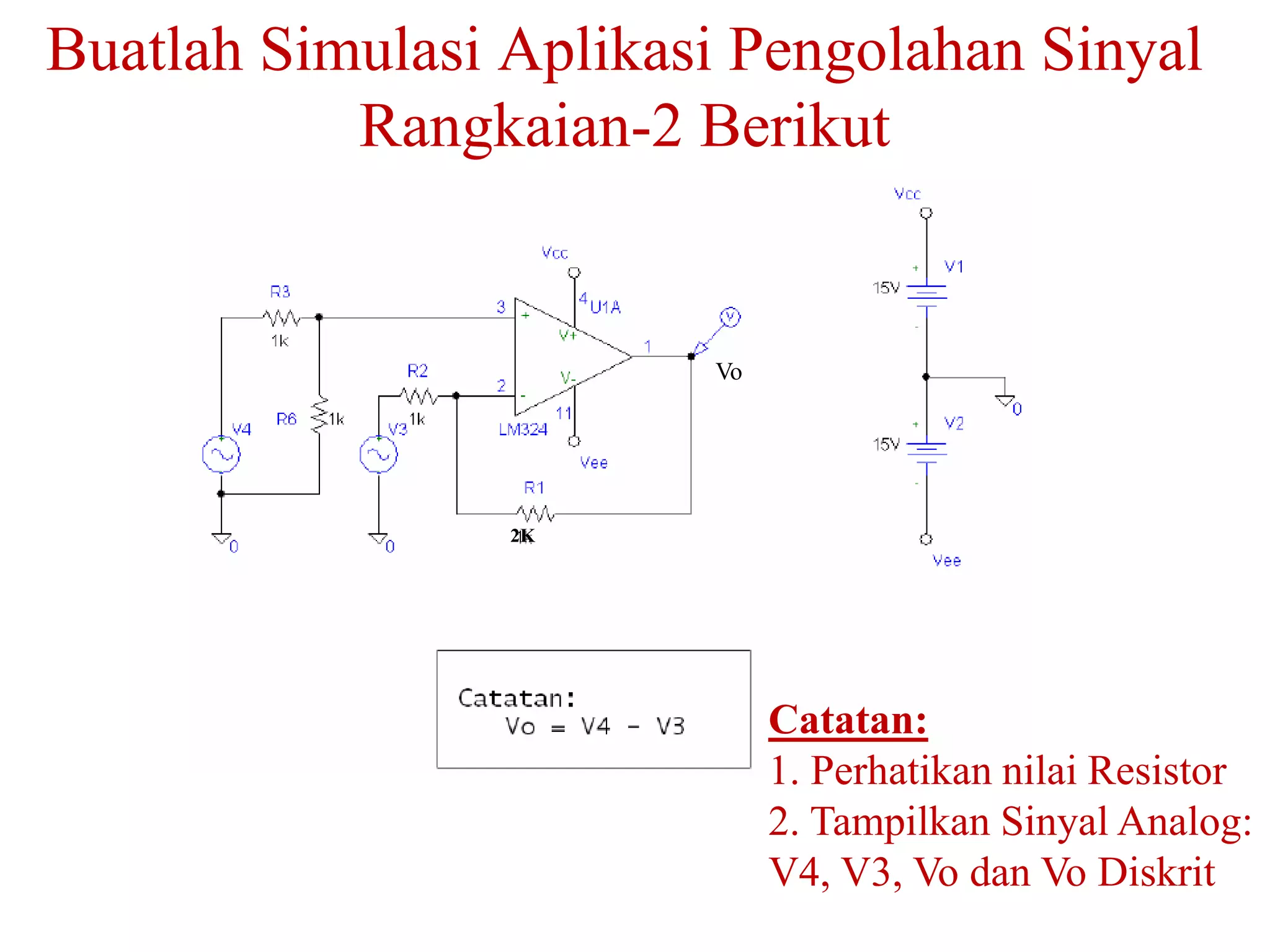
56. KONSEP FREKUENSI
 Sinyal sinusoidal waktu kontinu
 t)tcos(A)t(xa
F = frekuensi [siklus/detik, hertz (Hz)]
t = waktu
A = amplituda
 = frekuensi sudut[radian/detik]
 = fasa [radian]
)tF2cos(A)t(xF2 a 

57. )tcos(A)t(xa 
 Untuk setiap frekuensi F  xa(t) periodik
dasarperioda
F
1
T)t(x)Tt(x papa 
 Sinyal-sinyal sinusoidal waktu kontinu dengan frekuensi
berbeda dapat dibedakan
 Frekuensi diperbesar
Untuk suatu waktu tertentu jumlah perioda bertambah

58.  Sinyal sinusoidal waktu diskrit
 n)ncos(A)n(x
f = frekuensi [siklus/sampel]
n = bilangan bulat (integer)
A = amplituda
 = frekuensi [radian/sampel]
 = fasa [radian]
)nf2cos(A)n(xf2 

59. )nf2cos(A)n(x o 
 x (n) periodik hanya bila frekuensi f merupakan
bilangan rasional
)nf2cos(]Nf2nf2cos[])Nn(f2cos[
)n(x)Nn(x
oooo 

12
1
f
6
oo 


3


N
k
fk2Nf2 oo 
Harga terkecil dari N disebut perioda dasar

60.  Sinyal-sinyal sinusoidal waktu diskrit dengan frekuensi-
frekuensi yang berbeda sebanyak 2 k adalah identik
(tidak dapat dibedakan)
)ncos(]n2ncos[]n)2cos[( ooo 
k2
2,1,0k)ncos(A)n(x
ok
kk

 
2
1
f
2
1

 Frekuensi diperbesar  harga maksimum f = 1/2

63. f2 diganti 4 dan 8 dengan pha2 tetap

64. Output f2 diganti 4 dan 8 dg pha2 tetap

67. f2 diganti 4 dan 8
dg pha2 tetap

68. Output f2 diganti 4 dan 8 dg pha2 tetap

71. Adder Opamp

72. Sinyal Output Adder Opamp

74. Sinyal Keluaran Opamp ke 2

75. Secara umum konvolusi didefinisikan sebagai cara untuk
mengkombinasikan dua buah deret angka yang menghasilkan
deret angka yang ketiga.
Secara matematis, konvolusi adalah integral yang mencerminkan
jumlah lingkupan dari sebuah fungsi a yang digeser atas fungsi b
sehingga menghasilkan fungsi c. Konvolusi dilambangkan dengan
asterisk ( *).
Sehingga, a*b = c berarti fungsi a dikonvolusikan
dengan fungsi b menghasilkan fungsi c.
Fungsi Konvolusi adalah untuk ntuk menentukan hasil dari suatu
sinyal masukan ke sistem dapat menggunakan teknik konvolusi.

76. Persamaan Operasi Konvolusi

78. Dari hasil product and sum tersebut hasilnya dapat kita lihat
dalam bentuk deret sebagai berikut: 2 5 11 9 9

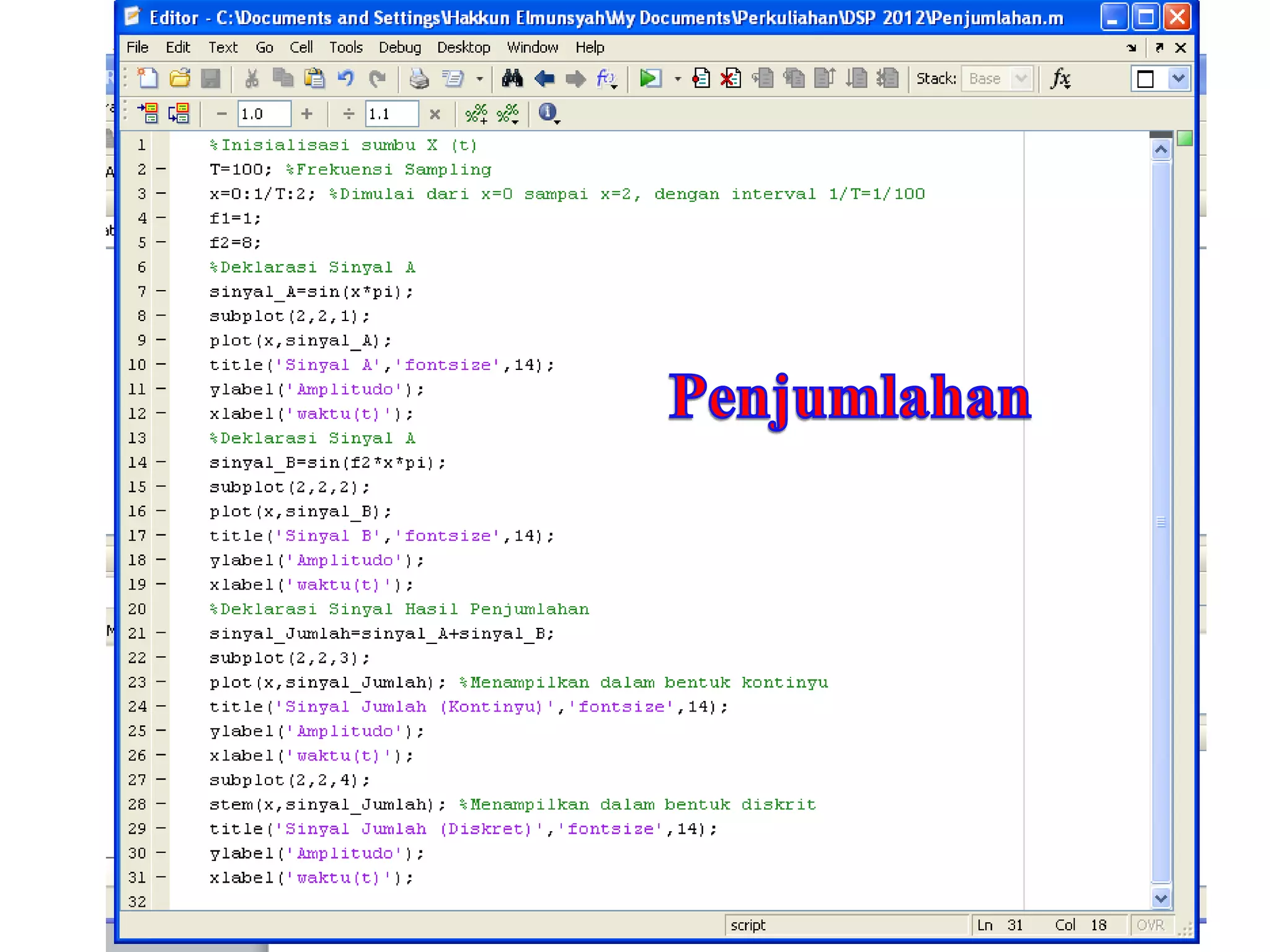
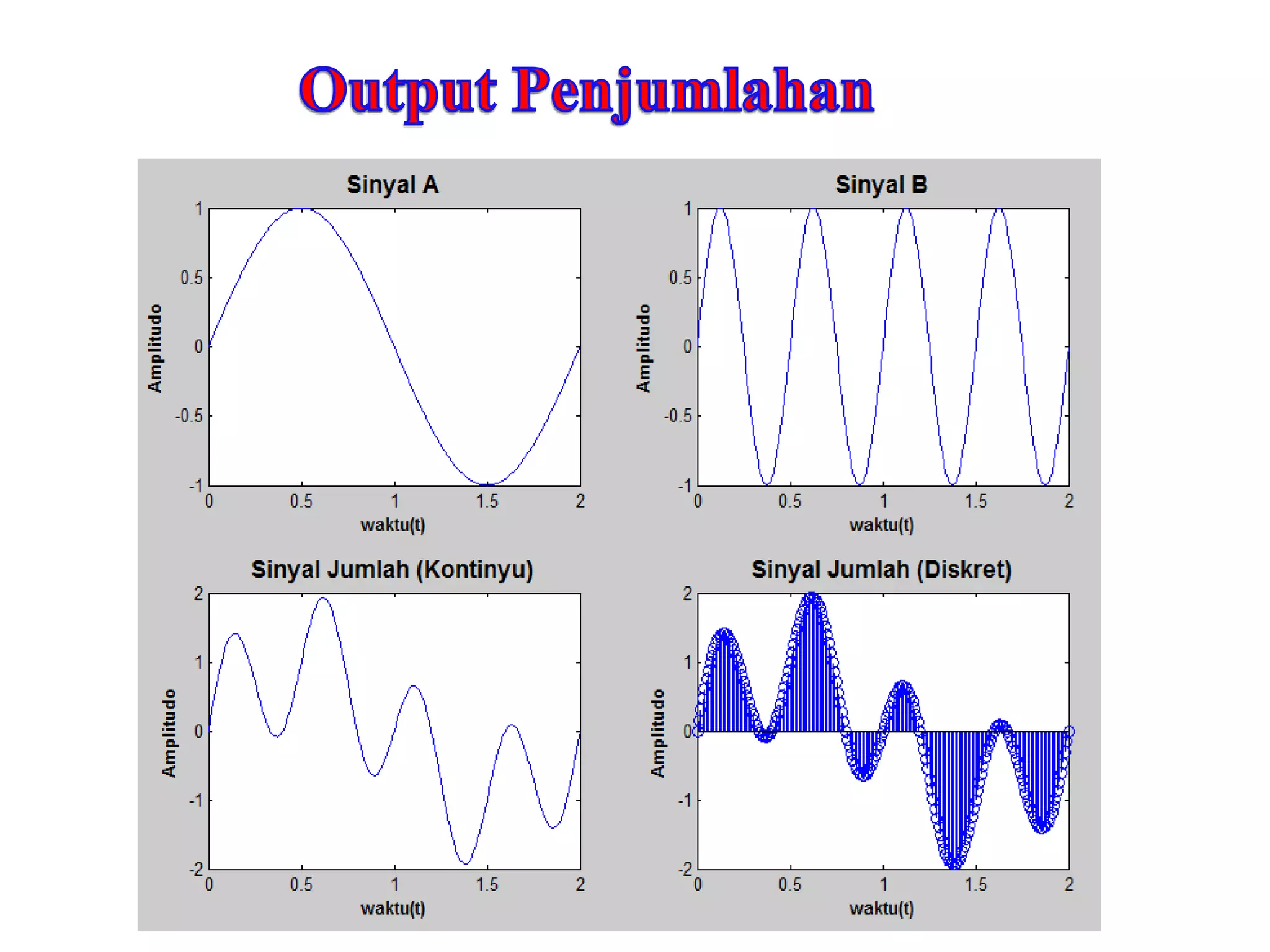
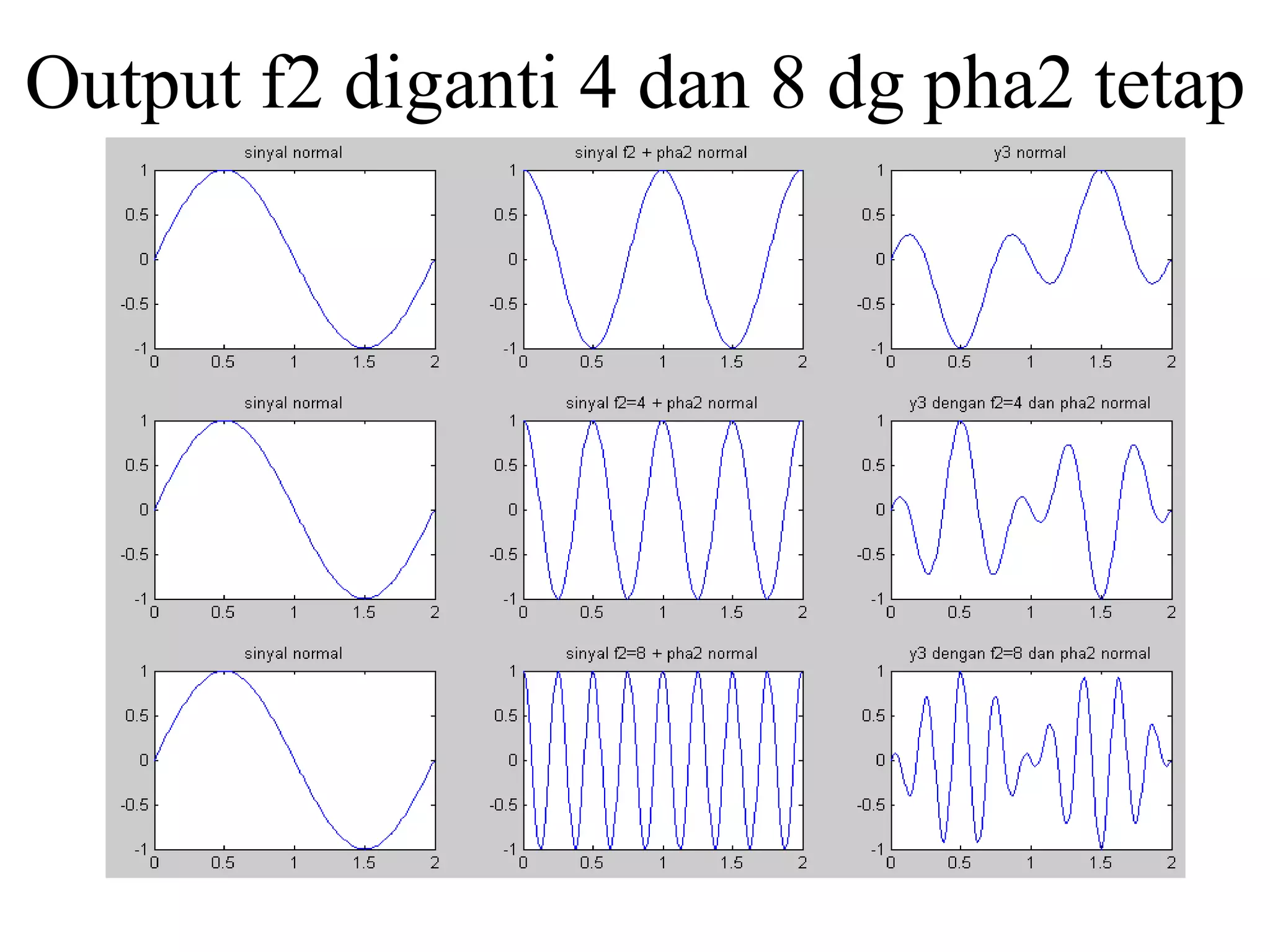
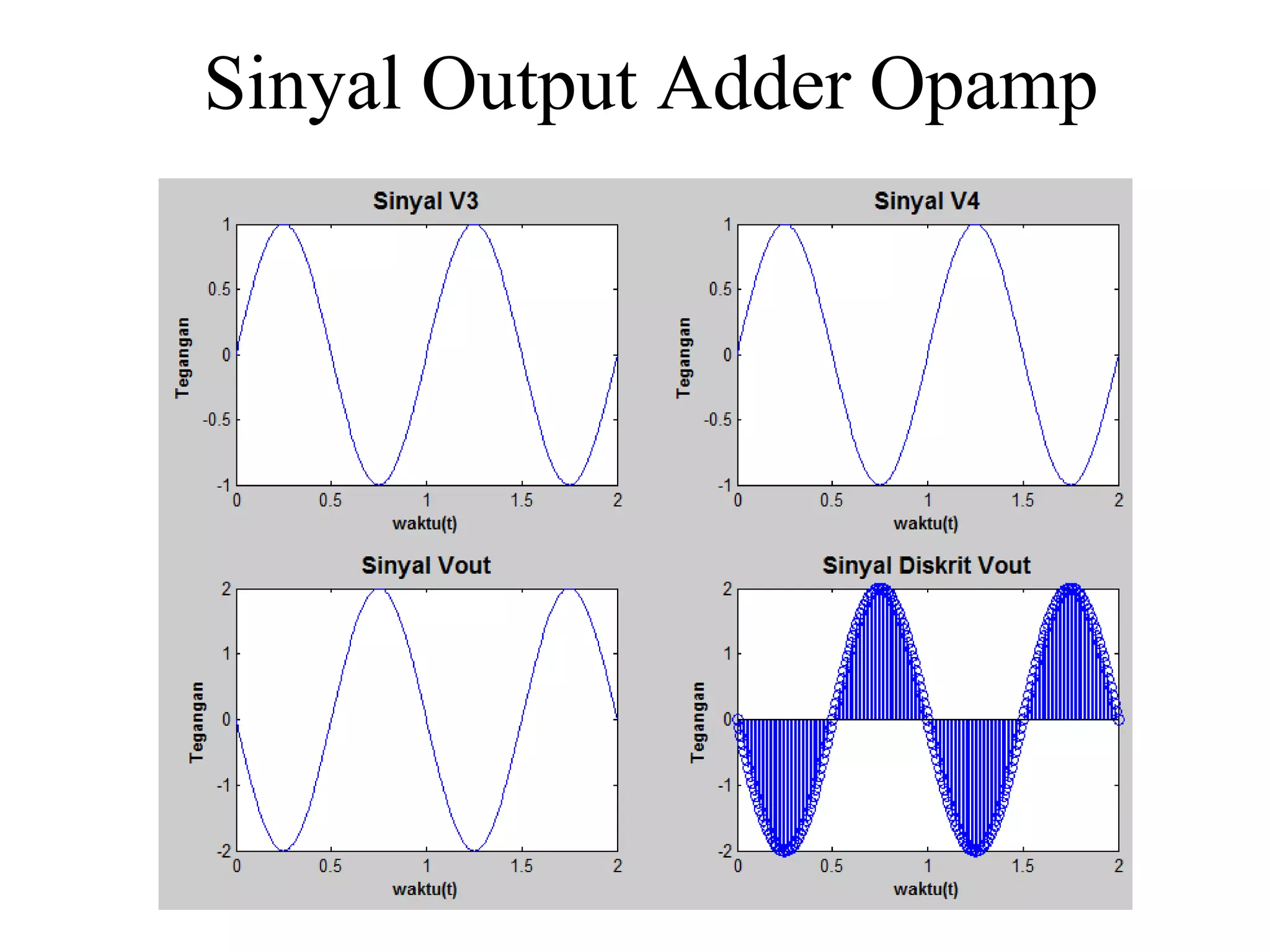
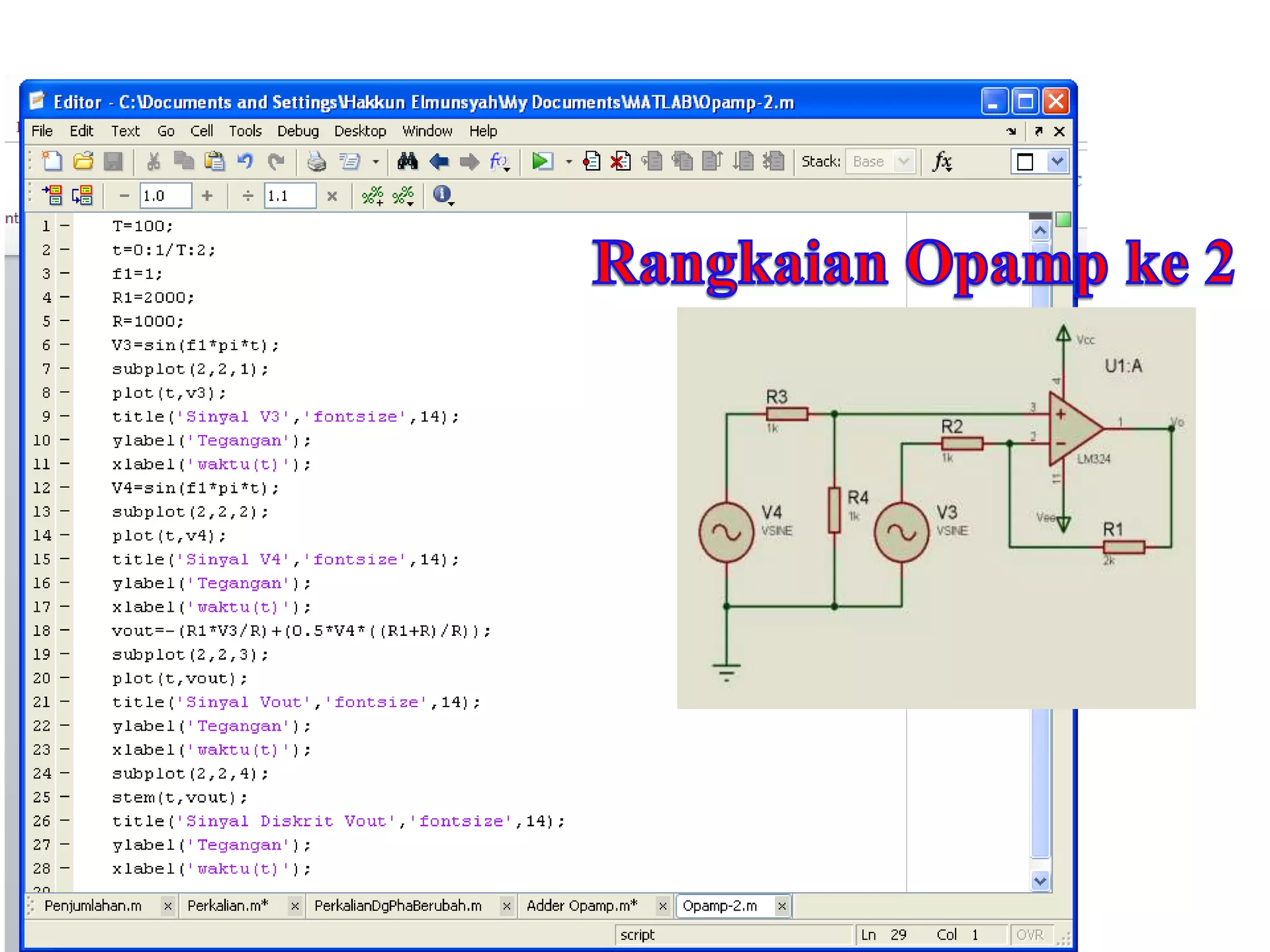
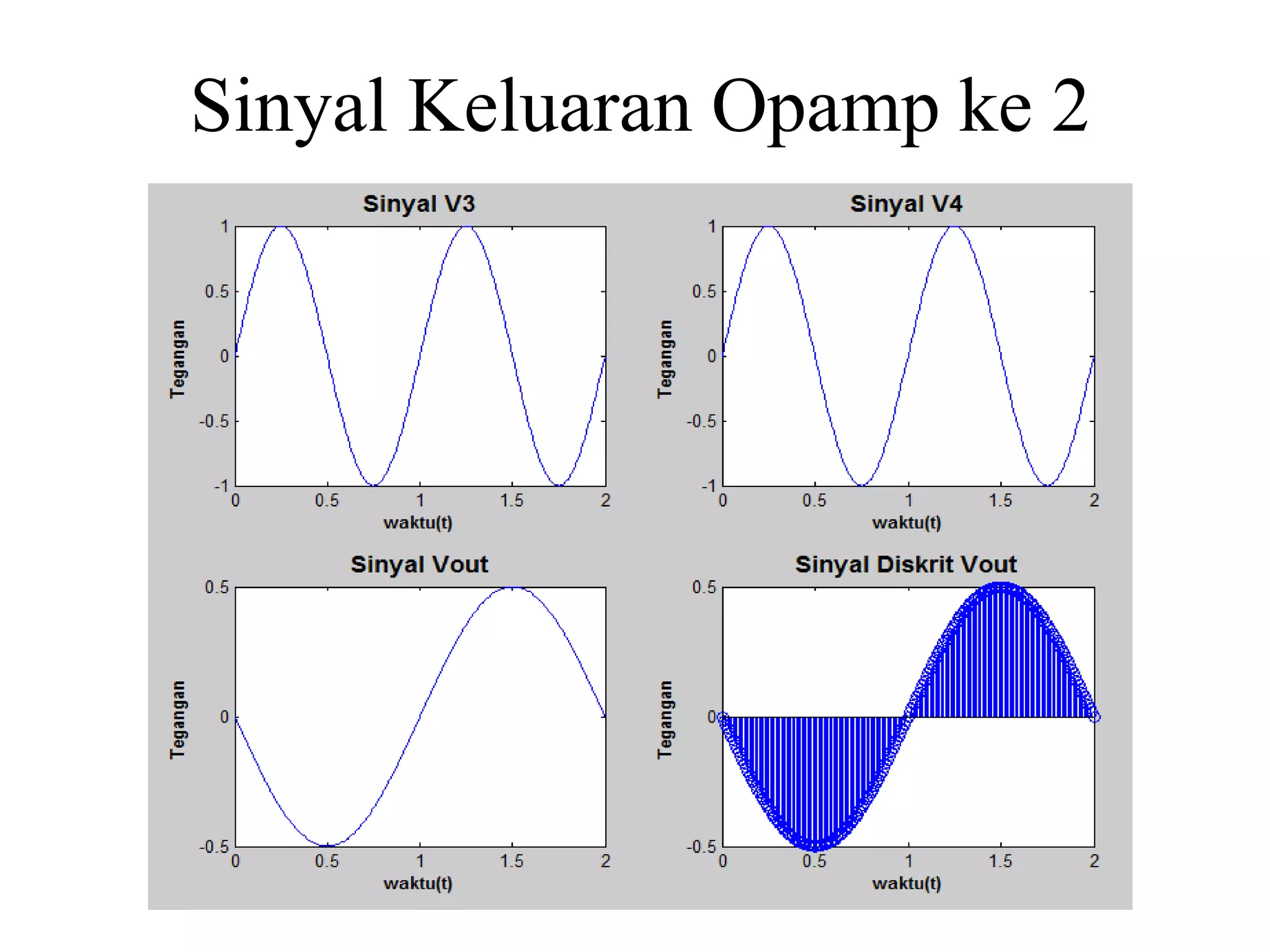
79. Script Matlab:
Pada gambar disamping ini,
menunjukkan sinyal x[n], bagian
kedua menunjukkan
sinyal v[n], sedangkan bagian
ketiga atau yang paling bawah
merupakan hasil konvolusi.

80. 1. Tentukan konvolusi
dari 2 fungsi sinyal
sebagai berikut
secara manual dan
Matlab:
a = [1 3 2 1 3 2 1 3 2]
b = [3 2 1]
2. Buktikan bahwa
secara manual dan
Matlab conv (a,b) dan
conv (b,a) dari sinyal
berikut adalah sama:
a=[1 3 2]
b=[3 2 1]

81. 3 11 13 10 13 13 10 13 13 7 2
Dari hasil product and sum tersebut hasilnya dapat kita lihat
dalam bentuk deret sebagai berikut:

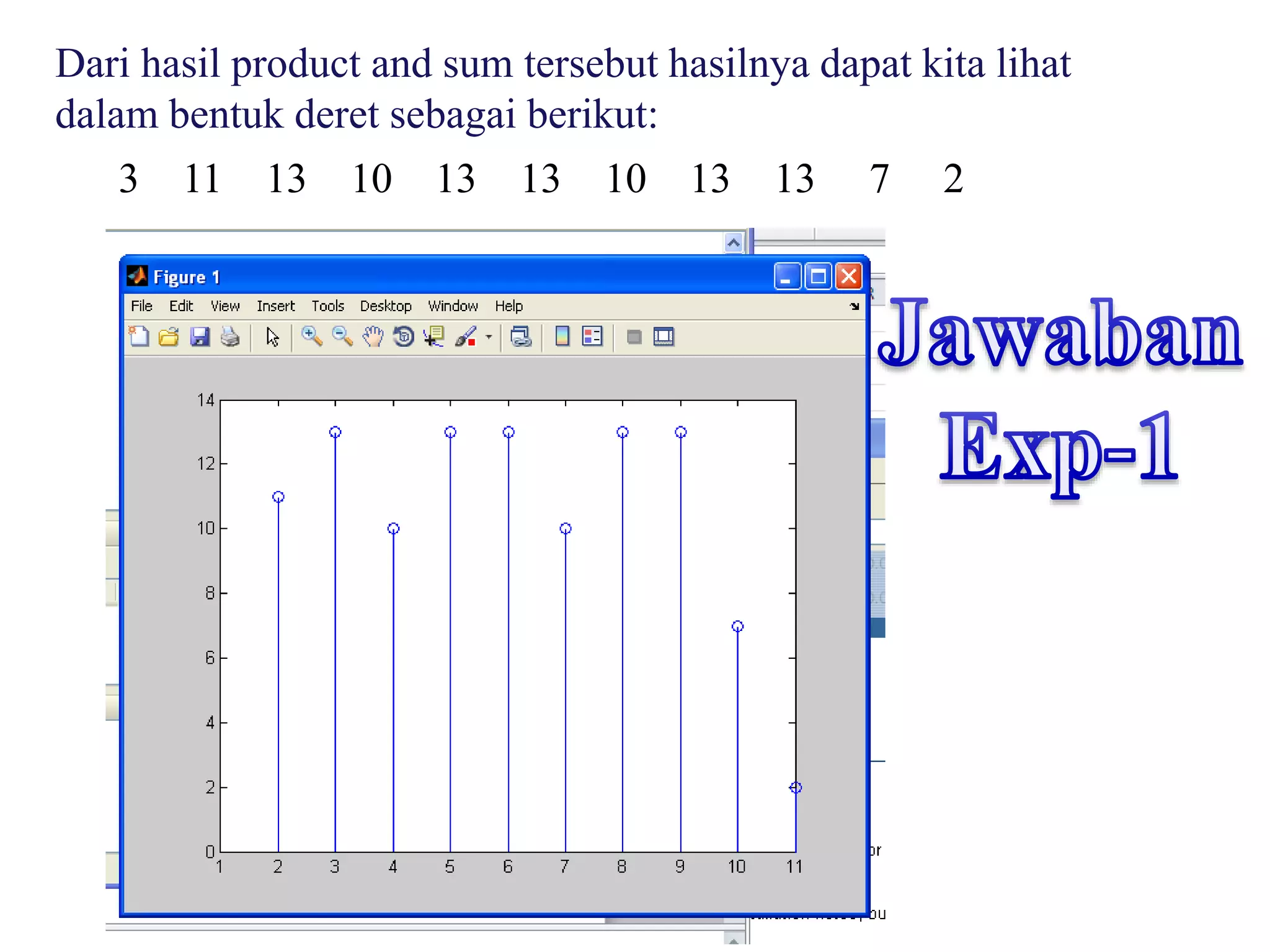
82. a=[1 3 2];
b=[3 2 1];
y1=conv(a,b);
y2=conv(b,a);
subplot (2,1,1);
stem (y1);
%title (‘Hasil y1’);
subplot (2,1,2);
stem (y2);
%title (‘Hasil y2’);

83. Scrip Experiment
a = [1 3 2 1 3 2 1 3 2];
b = [3 2 1];
y=conv(a,b)
stem (y)
a=[1 3 2];
b=[3 2 1];
Y1=conv(a,b)
Y2=conv(b,a)
Subplot (2,1,1);
Stem (y1);
Title (‘Hasil y1’)
Subplot (2,1,2);
Stem (y2);
Title (‘Hasil y2’)

84. Konsep dasar sinyal; Sistem dan pemrosesan
sinyal; Sinyal kontinyu dan diskrit;
Arithmatika sinyal; Operasi konvolusi.
Praktik pengolahan sinyal akustik, penguatan
dan pelemahan

85. Sinyal Akustik
Bunyi dapat terdengar oleh manusia apabila gelombang tersebut
mencapai telinga manusia dengan frekuensi 20Hz – 20kHz ,
suara ini disebut dengan audiosonic atau dikenal dengan audio,
gelombang suara pada batas frekuensi tersebut disebut dengan
sinyal akustik.
Bunyi atau suara dapat dibagi menjadi 4, yaitu:
1. Infrasound yaitu suara pada rentang frekuensi 0Hz-20Hz.
2. Audiosound yaitu suara pada rentang frekuensi 20Hz-20kHz.
3. Ultrasound yaitu suara pada rentang frekuensi 20kHz-1GHz.
4. Hypersound yaitu suara pada rentang frekuensi 1GHz-10THz.
Sumber: Yulid dan Fazmah (2006)

86. Pengolahan Sinyal Akustik
Dalam domain waktu, sinyal digambarkan dengan
bentuk waveform dimana sumbu-x menunjukkan
time dan sumbu-y menunjukkan besarnya amplitude
tiap waktu.
Berikut cara untuk merekam dan menganalisa sinyal
suara dengan software Matlab, antara lain dengan
perintah wavrecord dan audiorecorder.
Teknik tersebut mensyaratkan adanya souncard
yang telah terpasang, baik internal maupun
eksternal.

87. Pengolahan Sinyal Akustik
%Script pengolahan sinyal akustik
%Nama ……., NIM …….
Fs=8192; % deklarasi frekuensi sampling
y=wavrecord(5.0*Fs,Fs); % merekam suara selama lima detik
figure(1);
subplot (2,1,1);
plot(y); % menampilkan gelombang sinyal kontinyu
subplot (2,1,2);
Stem(y); % menampilkan gelombang sinyal diskrit
wavwrite(y,Fs,'Hakkun8192.wav') % menyimpan file .wav
1. Buat file script matlab sesuai dengan saudara, selanjutnya Amati
perubahan pada figure, suara melalui soundRecorder
2. Beri identitas hasil subplot dg title, xlabel dan ylabel
3. Ubah sampling sebesar 1K, beri file nama1K.wav.
4. Amati perubahan pd figure, suara dg soundRecorder, Bandingkan.

88. 5. Ubah sampling sebesar 16K, beri file nama16K.wav.
6. Amati perubahan pd figure, suara dg soundRecorder,
Bandingkan dg suara yang tersampling 8k dan 1k.
7. Ubah y=wavrecord(5.0*Fs,Fs); dg y=wavread(‘hakkun8192’);
beri diawal script terakhir dengan tanda % tambahkan
perintah seperti berikut ini:
y1=wavread(‘hakkun8192’);
penguat=2.0;
y2=penguat*y1
subplot (2,1,3);
plot(y2); % menampilkan gelombang sinyal yg dikuatkan
wavwrite(y2,Fs,'Hakkun8192x2.wav') % menyimpan file .wav
8. Amati perubahan pd figure, suara dg soundRecorder,
Bandingkan dg suara yang tersampling 8k.
9. Untuk lebih mengamati, rubah nilai penguat dg 0,1
selanjutnya amati sebagaimana langkah 8 diatas.

89. Mengubah Waveform Menjadi Spectrum
Transformasi yang mampu mengubah waveform menjadi spectrum
untuk mengetahui besarnya magnitude tiap waktu, dapat mengguna-
kan FFT atau Fast Fourier Transform. Berikut cara mengubah
waveform dari sinyal y hasil perekaman menjadi spectrum
sebagaimana script berikut:
fs=1024*8
z=wavread('Hakkun8192.wav');
Y=fft(z);
f=fs*(0:length(Y)-1)/length(Y);
figure(2);
plot(f,abs(Y));
title(’Kandungan frekuensi sinyal y
(gambar 2 sisi)’)
xlabel(’frekuensi (Hz)’);
ylabel(‘Magnitude’)