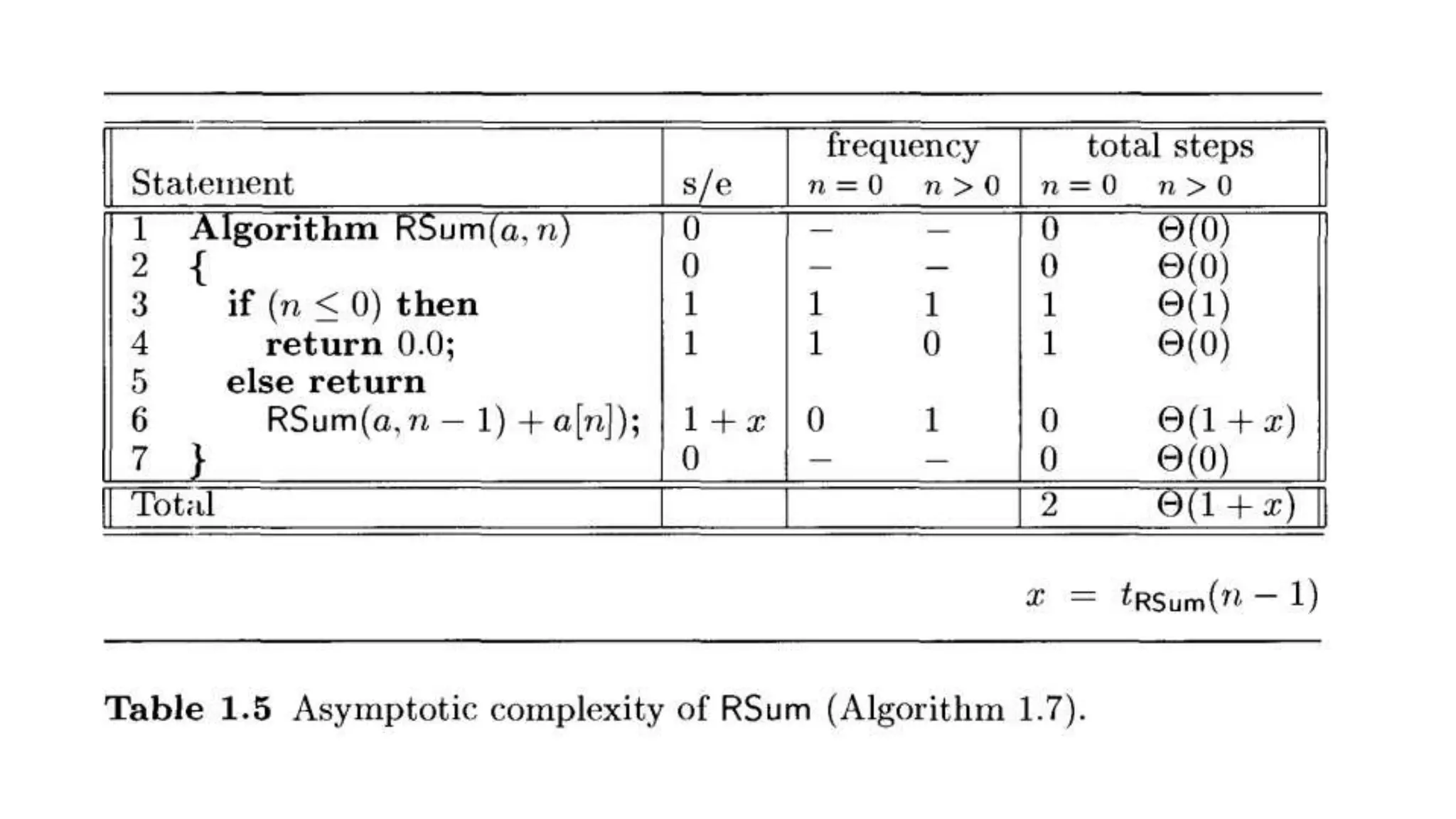
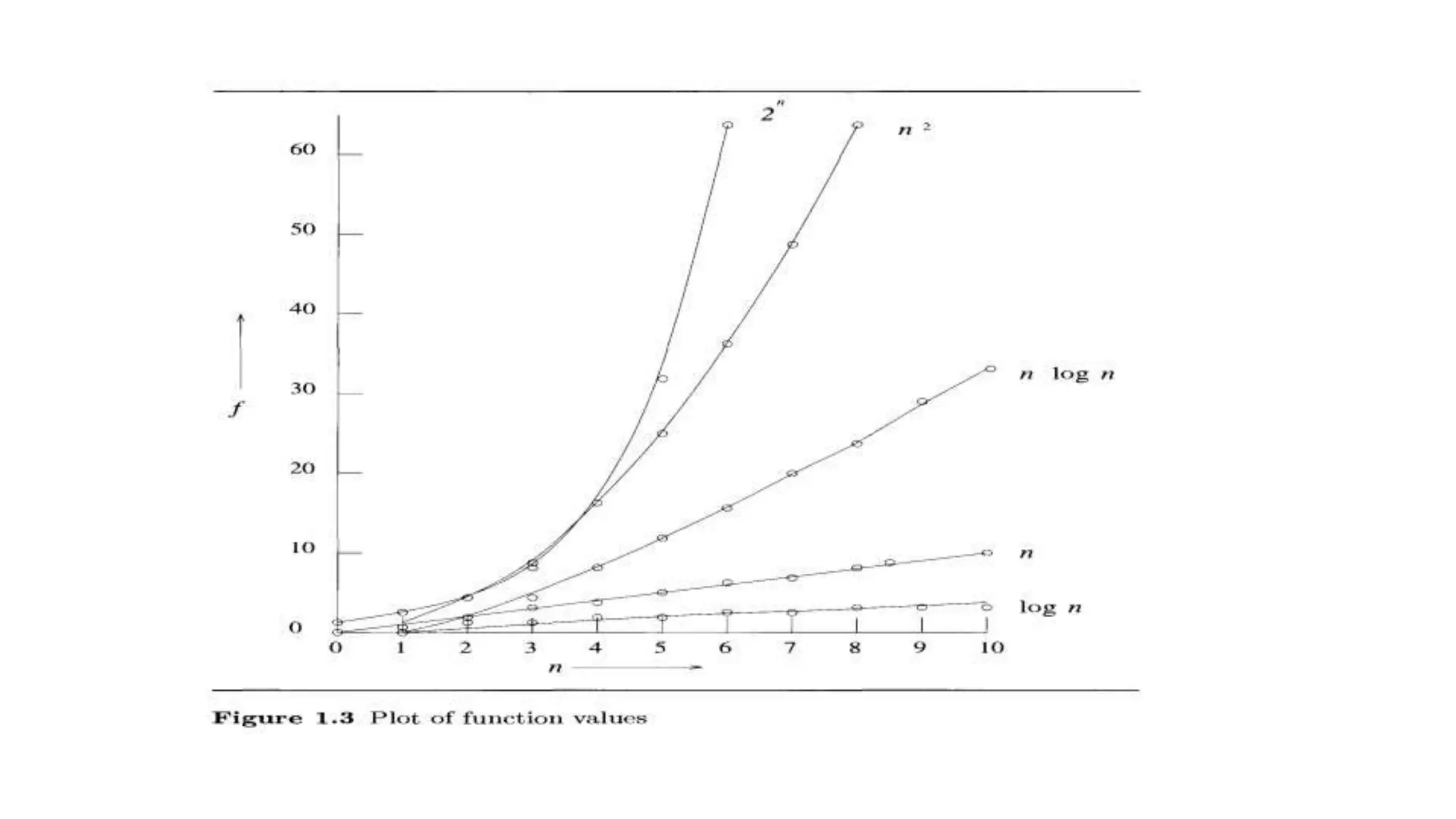
The document discusses different asymptotic notations used to characterize the complexity of algorithms: Big-O(O) notation provides an upper bound, Big-Omega(Ω) provides a lower bound, and Big-Theta(Θ) indicates the same order of growth. It defines each notation, explaining that Big-O represents f(n) growing less than or equal to g(n), Big-Omega represents f(n) growing greater than or equal to g(n), and Big-Theta represents f(n) growing equal to g(n). The document then discusses basics of probability theory, defining a sample space as the set of all possible outcomes of an experiment, with events being subsets of the sample space.

1. ALGORITHM DESIGN AND
ANALYSIS
SWAPNA.C

2. Asymptotic Notations
• Rate of Growth:
• The following notations are commonly use notations in performance
analysis and used to characterize the complexity of an algorithm:
• 1.Big–OH (O) 1,
• 2.Big–OMEGA ( ),
• 3.Big–THETA ( ) and
• 4.Little–OH (o)

3. Big–OH O (Upper Bound)
f(n) = O(g(n)), (pronounced order of or big oh), says that the growth rate of
f(n) is less than or equal (<) that of g(n).
Big ‘oh’: the function f(n)=O(g(n)) iff there exist positive constants c and no
such that f(n)≤c*g(n) for all n, n ≥ no.

5. Big–OMEGA Ω (Lower Bound)
f(n) = Ω (g(n)) (pronounced omega), says that the growth rate of f(n) is
greater than or equal to (>) that of g(n).
Omega: the function f(n)=Ω(g(n)) iff there exist positive constants c and no
such that f(n) ≥ c*g(n) for all n, n ≥ no.

6. Big–THETA ө (Same order)
f(n) = ө (g(n)) (pronounced theta), says that the growth rate of f(n)
equals (=) the growth rate of g(n) [if f(n) = O(g(n)) and T(n) = ө
(g(n)].
Theta: the function f(n)=ө(g(n)) iff there exist positive constants
c1,c2 and no such that c1 g(n) ≤ f(n) ≤ c2 g(n) for all n, n ≥ no.

13. RANDOMIZED ALGORITHMS
Basics of probability Theory: Probability theory has the goal of
characterizing the out comes of natural or conceptual "experiments”.
set of all possible outcomes is known as the sample space S.
In this text we assume that S is finite (such a sample spaceis called a
discrete sample
space).An event E is a subset of the sample space S.If the sample space
Consists of n sample points t,hen thereare2n possibel events.