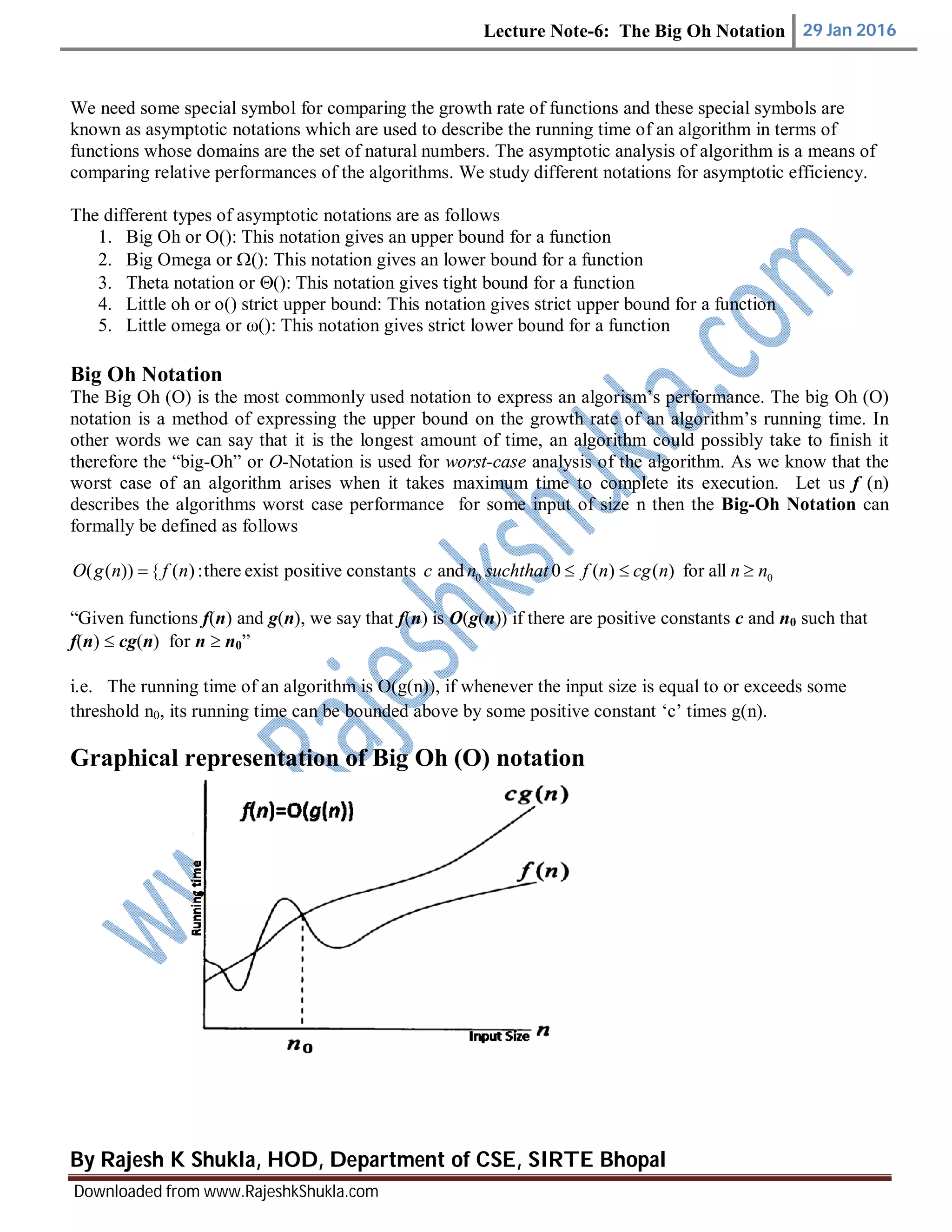
The document discusses Big O notation, which is used to describe the asymptotic upper bound of an algorithm's running time. It defines Big O notation formally as f(n) being O(g(n)) if there exist positive constants c and n0 such that f(n) is less than or equal to c * g(n) for all n greater than or equal to n0. The document provides examples of functions being Big O of other functions, such as 2n + 7 being O(n) and 2(n + 1) being O(2n). It explains that Big O notation characterizes the worst-case growth rate of an algorithm.

1. Lecture Note-6: The Big Oh Notation 29 Jan 2016
By Rajesh K Shukla, HOD, Department of CSE, SIRTE Bhopal
Downloaded from www.RajeshkShukla.com
We need some special symbol for comparing the growth rate of functions and these special symbols are
known as asymptotic notations which are used to describe the running time of an algorithm in terms of
functions whose domains are the set of natural numbers. The asymptotic analysis of algorithm is a means of
comparing relative performances of the algorithms. We study different notations for asymptotic efficiency.
The different types of asymptotic notations are as follows
1. Big Oh or O(): This notation gives an upper bound for a function
2. Big Omega or (): This notation gives an lower bound for a function
3. Theta notation or (): This notation gives tight bound for a function
4. Little oh or o() strict upper bound: This notation gives strict upper bound for a function
5. Little omega or ω(): This notation gives strict lower bound for a function
Big Oh Notation
The Big Oh (O) is the most commonly used notation to express an algorism’s performance. The big Oh (O)
notation is a method of expressing the upper bound on the growth rate of an algorithm’s running time. In
other words we can say that it is the longest amount of time, an algorithm could possibly take to finish it
therefore the “big-Oh” or O-Notation is used for worst-case analysis of the algorithm. As we know that the
worst case of an algorithm arises when it takes maximum time to complete its execution. Let us f (n)
describes the algorithms worst case performance for some input of size n then the Big-Oh Notation can
formally be defined as follows
00 allfor)()(0andconstantspositiveexistthere:)({))(( nnncgnfsuchthatncnfngO 
“Given functions f(n) and g(n), we say that f(n) is O(g(n)) if there are positive constants c and n0 such that
f(n)  cg(n) for n  n0”
i.e. The running time of an algorithm is O(g(n)), if whenever the input size is equal to or exceeds some
threshold n0, its running time can be bounded above by some positive constant ‘c’ times g(n).
Graphical representation of Big Oh (O) notation

2. Lecture Note-6: The Big Oh Notation 29 Jan 2016
By Rajesh K Shukla, HOD, Department of CSE, SIRTE Bhopal
Downloaded from www.RajeshkShukla.com
The Big Oh notation can also be proved by applying the limit formula as given below
If
)(
)(
lim ng
nf
n 
exists , then functions f(n) O(g(n)) if c
ng
nf
n

 )(
)(
lim such that 0<=c<∞
Big-Oh Notation can be summarized as follows
 The Big Oh-notation is an asymptotic upper bound on the growth of an algorithm
 The big-Oh notation is used widely to characterize algorithm’s running times
 f (n) and g(n) are functions over non-negative integers
 f (n) = O(g(n)) is read as “f (n) is Big Oh of g(n)”
 f (n) is O(g(n)) if f(n) is asymptotically less than or equal to g(n)
 The statement “f (n) is Big Oh of (g(n))” means that the growth rate of f (n) is no more than the
growth rate of g(n)
Example: 2n + 7 is O(n)
Proof: We have f(n) = 2n + 7 and g(n) =n when comparing it with f(n) =O(g(n))
From the definition of Big Oh, there must exist c>0, n0  1 and onn  such that    ncgnf 0 so
   ncgnf 0
0<=2n + 7  cn for all nЄN
This is true for c=3 and n0=7 therefore 2n + 7 is O(n)
The values of c and n0 are obtained as follows
(c  2) n  7>=0
n  7/(c  2) so we may choose c = 3 that results in n0 = 7
Example: 2(n + 1)
is O(2n
)
Proof: We have f(n) = 2(n + 1)
and g(n) =2n
when comparing it with f(n) =O(g(n))
From the definition of Big Oh, there must exist c>0, n0  1 and onn  such that    ncgnf 0 so 0<=2(n +
1)
 c2n
for any constant c and all onn  where n0 and nЄN
0<=2(n + 1)
 c.2n
this inequality holds for c=2 so
0<=2(n + 1)
 2.2n
Therefore 2(n + 1)
=O(2n
)
This can also be proved using the limit of functions
c
ng
nf
if
n

 )(
)(
lim
where 0<=c<∞
cn
n
n


 2
12
lim
cn
n
n

 2
2.2
lim
=2 (constant>0) hence 2(n + 1)
is O(2n
)