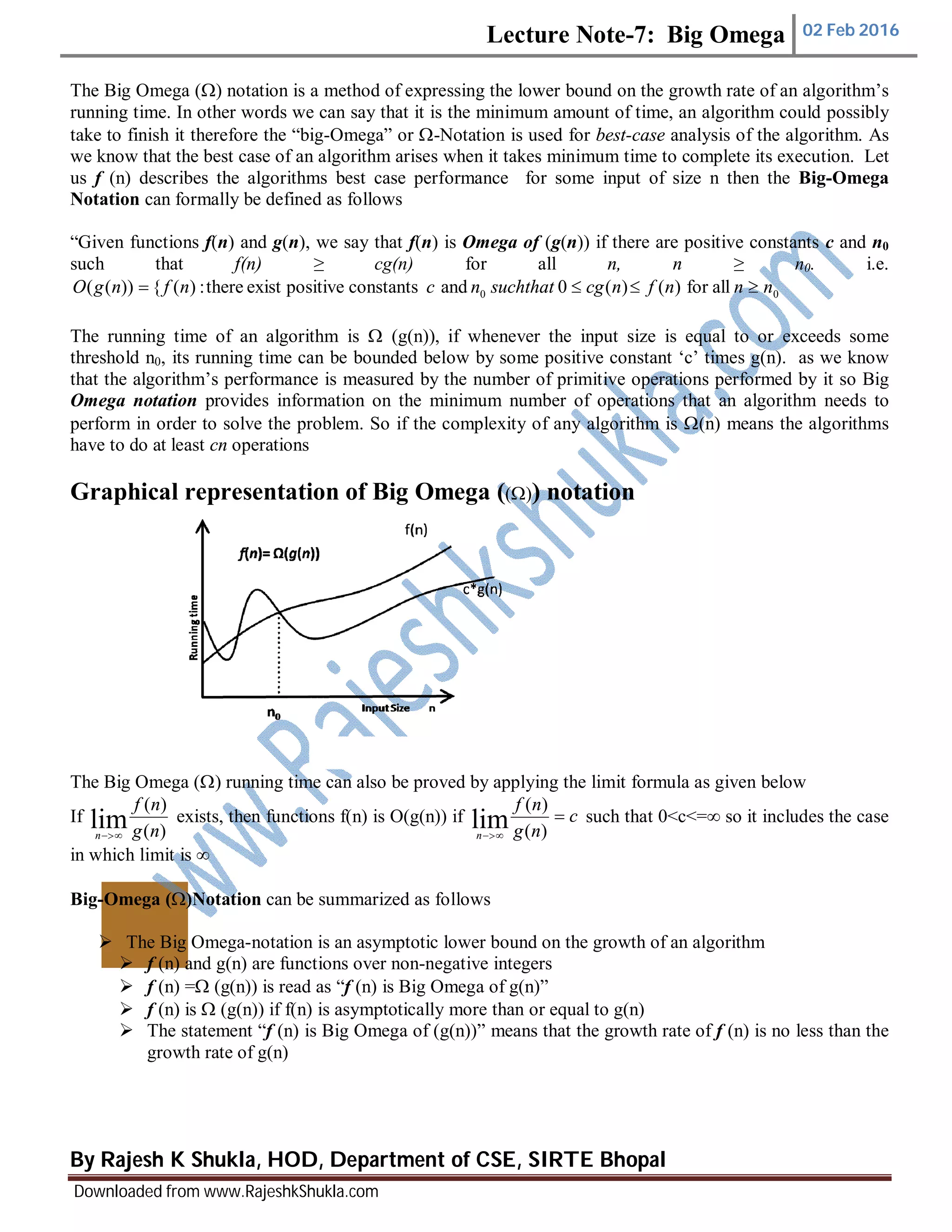
The document explains the big omega (Ω) notation, which represents the lower bound on the growth rate of an algorithm's running time, specifically for best-case analysis. It defines that f(n) is Ω(g(n)) if there are positive constants such that f(n) is greater than or equal to c * g(n) for sufficiently large n. Overall, big omega notation provides information on the minimum number of operations an algorithm must perform to solve a problem.

1. Lecture Note-7: Big Omega 02 Feb 2016
By Rajesh K Shukla, HOD, Department of CSE, SIRTE Bhopal
Downloaded from www.RajeshkShukla.com
The Big Omega () notation is a method of expressing the lower bound on the growth rate of an algorithm’s
running time. In other words we can say that it is the minimum amount of time, an algorithm could possibly
take to finish it therefore the “big-Omega” or -Notation is used for best-case analysis of the algorithm. As
we know that the best case of an algorithm arises when it takes minimum time to complete its execution. Let
us f (n) describes the algorithms best case performance for some input of size n then the Big-Omega
Notation can formally be defined as follows
“Given functions f(n) and g(n), we say that f(n) is Omega of (g(n)) if there are positive constants c and n0
such that f(n) ≥ cg(n) for all n, n ≥ n0. i.e.
00 allfor)()(0andconstantspositiveexistthere:)({))(( nnnfncgsuchthatncnfngO 
The running time of an algorithm is  (g(n)), if whenever the input size is equal to or exceeds some
threshold n0, its running time can be bounded below by some positive constant ‘c’ times g(n). as we know
that the algorithm’s performance is measured by the number of primitive operations performed by it so Big
Omega notation provides information on the minimum number of operations that an algorithm needs to
perform in order to solve the problem. So if the complexity of any algorithm is (n) means the algorithms
have to do at least cn operations
Graphical representation of Big Omega (()) notation
The Big Omega () running time can also be proved by applying the limit formula as given below
If
)(
)(
lim ng
nf
n 
exists, then functions f(n) is O(g(n)) if c
ng
nf
n

 )(
)(
lim such that 0<c<=∞ so it includes the case
in which limit is ∞
Big-Omega ()Notation can be summarized as follows
 The Big Omega-notation is an asymptotic lower bound on the growth of an algorithm
 f (n) and g(n) are functions over non-negative integers
 f (n) = (g(n)) is read as “f (n) is Big Omega of g(n)”
 f (n) is  (g(n)) if f(n) is asymptotically more than or equal to g(n)
 The statement “f (n) is Big Omega of (g(n))” means that the growth rate of f (n) is no less than the
growth rate of g(n)