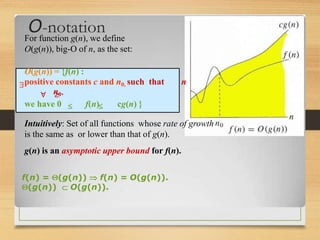
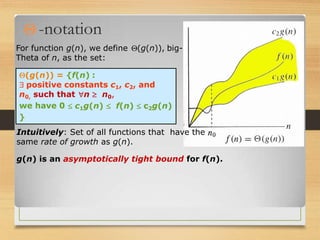
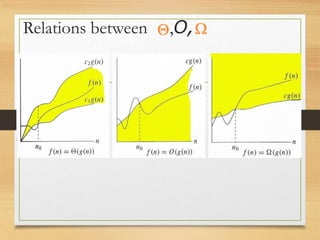
This document discusses asymptotic notation and its use in analyzing algorithms. It defines big O, Omega, and Theta notation and explains how they are used to describe the limiting behavior and growth rates of functions. Specifically, it explains that big O notation describes asymptotic upper bounds, Omega notation describes asymptotic lower bounds, and Theta notation describes asymptotically tight bounds. The document also discusses how these notations are used to analyze the time complexity of algorithms and classify their running times as inputs approach infinity.

1. Gandhinagar Institute of Technology
ADA(2150703)
Topic : Asymptotic Notation
Prepared By : Ravin
Laheri
Enrollment No :
160120107054
Batch : CE-B1
Guided By : Maitri
Patel

2. Introduction
In mathematics, computer science, and related fields, big O
notation describes the limiting behavior of a function when
the argument tends towards a particular value or infinity,
usually in terms of simpler functions. Big O notation allows
its users to simplify functions in order to concentrate on their
growth rates: different functions with the same growth rate
may be represented using the same O notation.
The time complexity of an algorithm quantifies the amount of
time taken by an algorithm to run as a function of the size of
the input to the problem. When it is expressed using big O
notation, the time complexity is said to be
described asymptotically, i.e., as the input size goes to infinity.

3. Asymptotic Complexity
Running time of an algorithm as a function of input size n for
large
n.
Expressed using only the highest-order term in the expression
for
the exact running time.
◦ Instead of exact running time, say (n2).
Describes behavior of function in the limit.
Written using Asymptotic Notation.
The notations describe different rate-of-growth relations
between
the defining function and the defined set of functions.

4. O-notationFor function g(n), we define
O(g(n)), big-O of n, as the set:
O(g(n)) = {f(n) :
positive constants c and n0, such that n
n0,
we have 0 f(n) cg(n) }
Intuitively: Set of all functions whose rate of growth
is the same as or lower than that of g(n).
g(n) is an asymptotic upper bound for f(n).
f(n) = O(g(n)).f(n) = (g(n))
(g(n)) O(g(n)).

5. -notation
f(n) = (g(n)).f(n) = (g(n))
(g(n)) (g(n)).
(g(n)) = {f(n) :
positive constants c and n0, such that
n n0,
we have 0 cg(n) f(n)}
Intuitively: Set of all functions whose rate
of growth is the same as or higher than that
of g(n).
g(n) is an asymptotic lower bound for
f(n).
(g(n)), big-For function g(n), we define
Omega of n, as the set:

6. -notation
(g(n)) = {f(n) :
positive constants c1, c2, and
c1g(n) f(n) c2g(n)
n0, such that n n0,
we have 0
}
(g(n)), big-For function g(n), we define
Theta of n, as the set:
Intuitively: Set of all functions that have the
same rate of growth as g(n).
g(n) is an asymptotically tight bound for f(n).

7. Relations between ,O,

8. Comparison of Functions
f g a b
f (n) = O(g(n))
f (n) = (g(n))
a
a
b
b
f (n) = (g(n)) a = b
f (n) = o(g(n)) a < b
f (n) = (g(n)) a > b

9. Running Times
“Running time is O(f(n))” Worst case is O(f(n))
O(f(n))
(f(n))
O(f(n)) bound on the worst-case running time
bound on the running time of every input.
(f(n)) bound on the worst-case running time
bound on the running time of every input.
“Running time is (f(n))” Best case is
Can still say “Worst-case running time is
(f(n))
(f(n))”
◦ Means worst-case running time is given by some
unspecified function g(n) (f(n)).