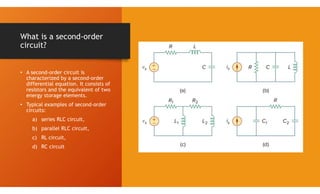
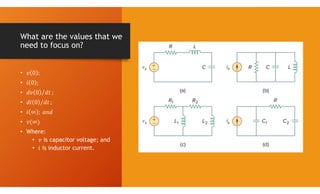
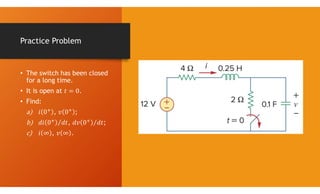
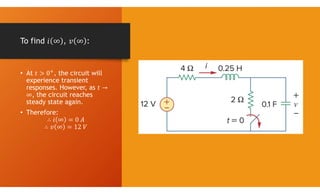
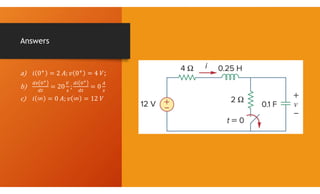
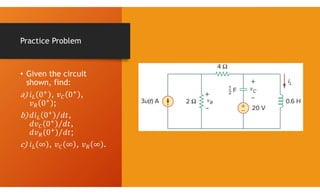
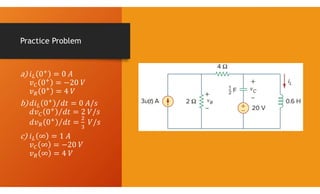
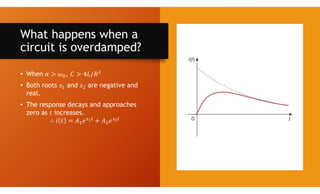
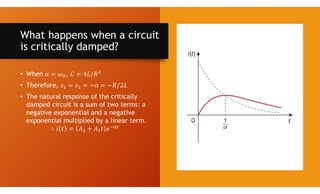
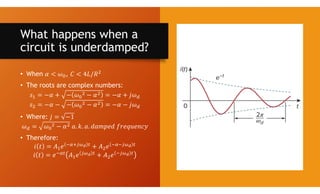
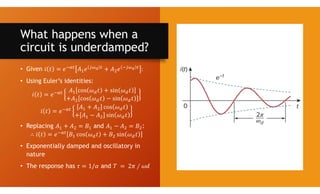
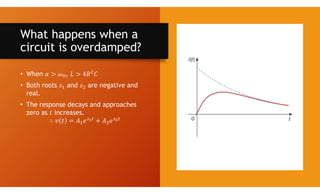
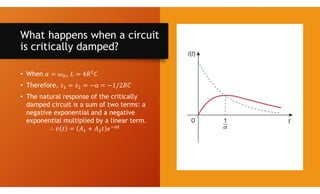
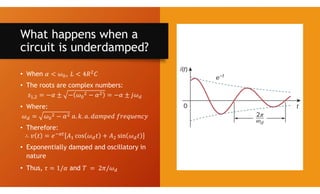
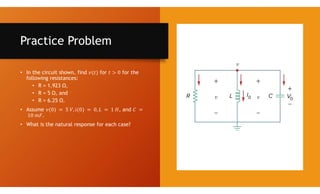
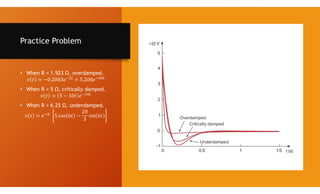
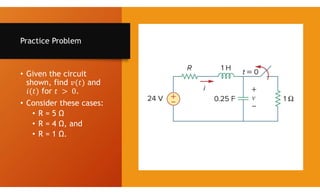
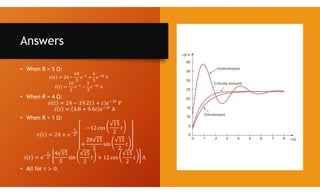
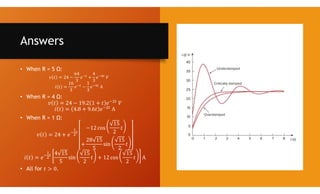
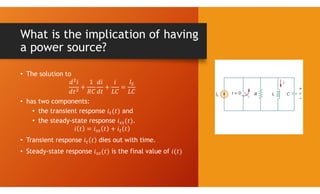
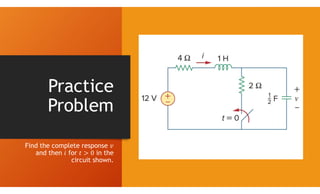
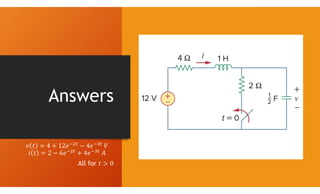
The document discusses second-order circuits, specifically source-free series and parallel RLC circuits, examining their characteristic equations and response types including overdamped, critically damped, and underdamped scenarios. It provides methods for finding initial and final values, and it presents practice problems for better understanding. The content elaborates on the transient and steady-state responses in terms of voltage and current variations in circuit conditions.

1. 6.1 Finding Initial and Final Values
6.2 The Source-Free Series RLC Circuit
6.3 The Source-Free Parallel RLC Circuit
6.4 Step Response of a Series RLC Circuit
6.5 Step Response of a Parallel RLC Circuit
6.6 General Second-Order Circuits
6. Second-Order Circuits

2. What is a second-order
circuit?
• A second-order circuit is
characterized by a second-order
differential equation. It consists of
resistors and the equivalent of two
energy storage elements.
• Typical examples of second-order
circuits:
a) series RLC circuit,
b) parallel RLC circuit,
c) RL circuit,
d) RC circuit

3. 6.1 Finding Initial and Final Values

4. What are the values that we
need to focus on?
•
•
•
•
•
•
• Where:
• is capacitor voltage; and
• is inductor current.

5. What are the key points to keep in mind in
determining the initial conditions?
1. As always in circuit
analysis—carefully handle
the polarity of voltage
across the capacitor and
the direction of the
current through the
inductor.
• and are defined strictly
according to the passive sign
convention.
• Carefully observe how these
are defined and apply them
accordingly.
2. Keep in mind that the capacitor voltage
is always continuous so that
and the inductor current is always continuous
so that
• Where
• denotes the time just before a
switching event and
• is the time just after the
switching event, assuming that the
switching event takes place at .

6. Practice Problems

7. Practice Problem
• The switch has been closed
for a long time.
• It is open at .
• Find:
, ;
, ;
, .

8. To find , :
• Since the switch has been closed for a long time
before , the circuit reached dc steady state.
• Therefore, at :
• Since the inductor current and the capacitor voltage
cannot change abruptly:

9. To find , :
• At , the switch opens. The same current flows
through both the inductor and capacitor.
• Hence, .
• Since
• Given use KVL to find :
• In the same manner that :

10. To find , :
• At , the circuit will
experience transient
responses. However, as
, the circuit reaches
steady state again.
• Therefore:

11. Answers
;

12. Practice Problem
• Given the circuit
shown, find:
, ,
;
,
,
;
, , .

13. To find , , :
• Since the switch has been closed for a long time
before , the circuit reached dc steady state.
• Therefore, at :
• Since the inductor current and the capacitor voltage
cannot change abruptly:

14. To find , , :
• Use KCL and KVL to find :
• KCL:
• KVL:
• Given that :

15. To find , , :
• Since :
• Given that , use KVL on the
rightmost mesh:
• Therefore:

16. To find , , :
• Since :
• Given and , use KCL on the
rightmost node:
• Therefore:

17. To find , , :
• To get , use KCL at the leftmost node:
• Taking the derivative of each term when :
• Applying KVL to middle mesh:
• Again, taking derivative of each term when :

18. To find , , :
• Substitute 𝑑𝑣 0 /𝑑𝑡 = 2 𝑉/𝑠 to the KVL equation:
−
𝑑𝑣 0
𝑑𝑡
+
𝑑𝑣 0
𝑑𝑡
+ 2 = 0;
𝑑𝑣 0
𝑑𝑡
−
𝑑𝑣 0
𝑑𝑡
= 2
• Given 0 = 2 + , substitute:
2
𝑑𝑣 0
𝑑𝑡
= −
𝑑𝑣 0
𝑑𝑡
;
𝑑𝑣 0
𝑑𝑡
−
𝑑𝑣 0
𝑑𝑡
= 2
𝑑𝑣 0
𝑑𝑡
+ 2
𝑑𝑣 0
𝑑𝑡
= 2; 3
𝑑𝑣 0
𝑑𝑡
= 2
∴
𝑑𝑣 0
𝑑𝑡
=
2
3
𝑉/𝑠
• Had we been looking for 𝑑𝑖 0 /𝑑𝑡, use 𝑣 = 2𝑖 :
𝑑𝑖 0
𝑑𝑡
=
1
2
𝑑𝑣 0
𝑑𝑡
=
1
2
×
2
3
=
1
3
𝐴/𝑠

19. To find , , :
• At , the circuit will experience transient
responses. However, as , the circuit reaches
steady state again. The 3-A current source is now
working on the circuit.
• Therefore:

20. Practice Problem

21. Thank You!

22. 6.1 Finding Initial and Final Values
6.2 The Source-Free Series RLC Circuit
6.3 The Source-Free Parallel RLC Circuit
6.4 Step Response of a Series RLC Circuit
6.5 Step Response of a Parallel RLC Circuit
6.6 General Second-Order Circuits
6. Second-Order Circuits

23. 6.2 The Source-Free Series RLC Circuit

24. Why is this considered a second-
order differential equation?
• Using KVL:
• Given and letting ,
differentiate:
• This is the series RLC circuit’s characteristic
equation.

25. How can this be simplified?
• Given , determine the roots:
or
• Where:
• The roots and are the natural frequencies of the
circuit.
• The resonant frequency is strictly referred to as the
undamped natural frequency of the circuit.

26. What is the implication of having
two roots?
• In simple terms, there are three solutions.
• Response vs. roots of circuit’s characteristic equation:
1. If overdamped, or unequal and real
2. If critically damped, or equal and real
3. If underdamped, or complex

27. What happens when a
circuit is overdamped?
• When ,
• Both roots and are negative and
real.
• The response decays and approaches
zero as increases.

28. What happens when a circuit
is critically damped?
• When ,
• Therefore,
• The natural response of the critically
damped circuit is a sum of two terms: a
negative exponential and a negative
exponential multiplied by a linear term.

29. What happens when a
circuit is underdamped?
• When ,
• The roots are complex numbers:
• Where:
• Therefore:

30. What happens when a
circuit is underdamped?
• Given
• Using Euler’s identities:
• Replacing and :
• Exponentially damped and oscillatory in
nature
• The response has and

31. Practice Problems

32. Practice Problem
• Given R = 40 Ω, L = 4 H, and C = 1∕4 F:
• Calculate the characteristic roots of the circuit.
• Is the natural response overdamped, underdamped,
or critically damped?
• Find where , and .

33. Solution
• Given R = 40 Ω, L = 4 H, and C = 1∕4 F:
• Find:
,
• Since , the response is overdamped. Thus:

34. Solution
• Given , obtain
and using , and :
• At :
• Given R = 40 Ω, L = 4 H, and C = 1∕4 F, use KVL:

35. Solution
• Given , take the derivative of :
• At :

36. Solution
• Given:
• Get and :
• Answer:
• Therefore:

37. Answers
• The characteristic roots of the circuit are:
• Since , the response is overdamped.
• where , and is:

38. Practice Problem
• Find in the circuit.
• Assume that the circuit has reached steady state at
.

39. Solution
• For , the switch is closed. Thus, at
• For , the switch is opened, and the voltage
source is disconnected.
,
• Since , the response is underdamped.

40. Solution
• Given that response is underdamped, , and
:
• Obtain and using and :
• At : ( )
• Using KVL:

41. Solution
• Given and , take the derivative of
•
• At :
( )
• Therefore:

42. Thank You!

43. 6.1 Finding Initial and Final Values
6.2 The Source-Free Series RLC Circuit
6.3 The Source-Free Parallel RLC Circuit
6.4 Step Response of a Series RLC Circuit
6.5 Step Response of a Parallel RLC Circuit
6.6 General Second-Order Circuits
6. Second-Order Circuits

44. 6.3 The Source-Free Parallel RLC Circuit

45. Why is this considered a second-
order differential equation?
• Using KCL:
• The parallel RLC circuit’s characteristic equation is:
• Therefore:
, or ,
• Where:

46. What is the implication of having
two roots?
• In simple terms, there are three solutions.
• Response vs. roots of circuit’s characteristic
equation:
• If overdamped, or unequal and real
• If critically damped, or equal and real
• If underdamped, or complex

47. What happens when a
circuit is overdamped?
• When ,
• Both roots and are negative and
real.
• The response decays and approaches
zero as increases.

48. What happens when a circuit
is critically damped?
• When ,
• Therefore,
• The natural response of the critically
damped circuit is a sum of two terms: a
negative exponential and a negative
exponential multiplied by a linear term.

49. What happens when a
circuit is underdamped?
• When ,
• The roots are complex numbers:
,
• Where:
• Therefore:
• Exponentially damped and oscillatory in
nature
• Thus, and

50. Practice Problems

51. Practice Problem
• In the circuit shown, find 𝑣(𝑡) for 𝑡 > 0 for the
following resistances:
• R = 1.923 Ω,
• R = 5 Ω, and
• R = 6.25 Ω.
• Assume 𝑣(0) = 5 𝑉, 𝑖(0) = 0, 𝐿 = 1 𝐻, and 𝐶 =
10 𝑚𝐹.
• What is the natural response for each case?

52. If R = 1.923 Ω:
• Given , and :
,
,
• Since , the response is overdamped.
• Thus:

53. If R = 1.923 Ω:
• Given , obtain and
using and :
• At :
• Given , and , use KCL:

54. If R = 1.923 Ω:
• Given and , take the
derivative of
• At :
• Get and :
• Answer:
• Therefore:

55. If R = 5 Ω:
• Given , and :
,
,
• Since , the response is critically damped.
• Thus:

56. If R = 5 Ω:
• Given , obtain and
using and :
• At :
• Given , and , use KCL:

57. If R = 5 Ω:
• Given and , take the
derivative of
• At :
• Get and :
• Therefore:

58. If R = 6.25 Ω:
• Given , and :
,
,
• Since , the response is underdamped.
• Thus:

59. If R = 6.25 Ω:
• Given , obtain
and using and :
• At :
• Given , and , use KCL:

60. If R = 6.25 Ω:
• Given and , take the derivative
of
•
• At :
•
• Get and :
• Therefore:

61. Practice Problem
• When R = 1.923 Ω, overdamped.
𝑣 𝑡 = −0.2083𝑒 + 5.208𝑒
• When R = 5 Ω, critically damped.
𝑣 𝑡 = 5 − 50𝑡 𝑒
• When R = 6.25 Ω, underdamped.
𝑣 𝑡 = 𝑒 5 cos 6𝑡 −
20
3
sin 6𝑡

62. Practice
Problem
Find for in the RLC
circuit.

63. Solution
• For , the switch is open. Thus, at
• For , the switch is closed, and the voltage source is
disconnected.
,
• Since , the response is overdamped.
• Thus:

64. Solution
• Given , obtain
and using and :
• At :
• Use KCL:
. .
.

65. Solution
• Given and , take the derivative
of
•
• At :
• Get and :
• Answer:
• Therefore:

66. Thank You!

67. 6.1 Finding Initial and Final Values
6.2 The Source-Free Series RLC Circuit
6.3 The Source-Free Parallel RLC Circuit
6.4 Step Response of a Series RLC Circuit
6.5 Step Response of a Parallel RLC Circuit
6.6 General Second-Order Circuits
6. Second-Order Circuits

68. 6.4 Step Response of a Series RLC Circuit

69. Why is this considered a second-
order differential equation?
• Using KVL:
• Replace every with :
• The series RLC circuit’s characteristic equation is still:
• Therefore:
, or ,
• Where:

70. What is the implication of having
two roots?
• In simple terms, there are three solutions.
• Response vs. roots of circuit’s characteristic
equation:
• If overdamped, or unequal and real
• If critically damped, or equal and real
• If underdamped, or complex

71. What is the implication of having
a power source?
• The solution to
• has two components:
• the transient response and
• the steady-state response .
• Steady-state response is the final value of
• Transient response dies out with time.

72. How is the steady-state response
obtained?
• Steady-state response is the final value of .
• In the circuit shown, the final value of the capacitor
voltage is the same as the source voltage .
• Therefore:

73. How is the transient response
obtained?
• Transient response is the solution for the source-
free circuit.
• Thus, the transient response for the overdamped,
underdamped, and critically damped cases are:
• Overdamped:
• Critically damped:
• Underdamped:

74. How is the complete response
obtained?
• Given that , the complete
solution for the overdamped, underdamped, and
critically damped cases are:
• Overdamped:
• Critically damped:
• Underdamped:

75. Practice Problems

76. Practice Problem
• Given the circuit
shown, find and
for .
• Consider these cases:
• R = 5 Ω
• R = 4 Ω, and
• R = 1 Ω.

77. Answers
• When R = 5 Ω:
𝑣 𝑡 = 24 −
64
3
𝑒 +
4
3
𝑒 𝑉
𝑖 𝑡 =
16
3
𝑒 −
1
3
𝑒 A
• When R = 4 Ω:
• When R = 1 Ω:
• All for .

78. If R = 5 Ω:
• For , the switch is closed. Thus, at
• For , the switch is opened, and the 1-ohm resistor
is disconnected.
,
• Since , the response is overdamped. Thus:

79. If R = 5 Ω:
• Given obtain , and
using and :
• At :
• At :
• Find :
• Take the derivative of :
• At :

80. If R = 5 Ω:
• Given and :
• Get and :
• Answer:
• Therefore:
• Find :

81. If R = 4 Ω:
• For , the switch is closed. Thus, at
• For , the switch is opened, and the 1-ohm resistor
is disconnected.
,
• Since , the response is critically damped. Thus:

82. If R = 4 Ω:
• Given obtain , and
using and :
• At :
• At :
• Find :
• Take the derivative of :
• At :

83. If R = 4 Ω:
• Given
• Therefore:
• Find :

84. If R = 1 Ω:
• For , the switch is closed. Thus, at
• For , the switch is opened, and the 1-ohm resistor
is disconnected.
,
• Since , the response is underdamped. Thus:

85. If R = 1 Ω:
• Given
obtain , and using and :
• At :
• At :
• Find :

86. If R = 1 Ω:
• Given and , take the derivative of
:
• At :

87. If R = 1 Ω:
• Given
𝐴
𝐴
=
−12
=
−12
21.69
• Therefore: ∴ 𝑣 𝑡 = 24 + 𝑒 −12 cos 𝑡 + sin 𝑡
• Find 𝑖 𝑡 : 𝑖 𝑡 = 𝐶 𝑑𝑣/𝑑𝑡
𝑖 𝑡 = 0.25
𝑑
𝑑𝑡
24 + 𝑒 −12 cos
15
2
𝑡 +
28 15
5
sin
15
2
𝑡
𝑖 𝑡 =
1
4
−
1
2
𝑒 −12 cos
15
2
𝑡 +
28 15
5
sin
15
2
𝑡
+
15
2
𝑒 12 sin
15
2
𝑡 +
28 15
5
cos
15
2
𝑡
𝑖 𝑡 =
1
4
×
1
2
𝑒 12 15 −
28 15
5
sin
15
2
𝑡 + 12 + 84 cos
15
2
𝑡
𝑖 𝑡 =
1
4
×
1
2
𝑒
32 15
5
sin
15
2
𝑡 + 96 cos
15
2
𝑡
∴ 𝑖 𝑡 = 𝑒
4 15
5
sin
15
2
𝑡 + 12 cos
15
2
𝑡 A

88. Answers
• When R = 5 Ω:
𝑣 𝑡 = 24 −
64
3
𝑒 +
4
3
𝑒 𝑉
𝑖 𝑡 =
16
3
𝑒 −
1
3
𝑒 A
• When R = 4 Ω:
• When R = 1 Ω:
• All for .

89. Thank You!

90. 6.1 Finding Initial and Final Values
6.2 The Source-Free Series RLC Circuit
6.3 The Source-Free Parallel RLC Circuit
6.4 Step Response of a Series RLC Circuit
6.5 Step Response of a Parallel RLC Circuit
6.6 General Second-Order Circuits
6. Second-Order Circuits

91. 6.5 Step Response of a Parallel RLC Circuit

92. Why is this considered a second-
order differential equation?
• Using KCL:
• Replace every with :
• The parallel RLC circuit’s characteristic equation is still:
• Therefore:
, or ,
• Where:

93. What is the implication of having
two roots?
• In simple terms, there are three solutions.
• Response vs. roots of circuit’s characteristic
equation:
• If overdamped, or unequal and real
• If critically damped, or equal and real
• If underdamped, or complex

94. What is the implication of having
a power source?
• The solution to
• has two components:
• the transient response and
• the steady-state response .
• Transient response dies out with time.
• Steady-state response is the final value of

95. How is the steady-state response
obtained?
• Steady-state response is the final value of
.
• In the circuit shown, the final value of the inductor
current is the same as the current source .
• Therefore:

96. How is the transient response
obtained?
• Transient response is the solution for the source-
free circuit.
• Thus, the transient response for the overdamped,
underdamped, and critically damped cases are:
• Overdamped:
• Critically damped:
• Underdamped:

97. How is the complete response
obtained?
• Given that , the complete solution
for the overdamped, underdamped, and critically
damped cases are:
• Overdamped:
• Critically damped:
• Underdamped:

98. Practice Problems

99. Practice
Problem
Given the circuit shown, find
and for .

100. Solution
• For , the switch is open and the 30-V source is on.
Thus, at
• For , the switch is closed and 30-V source is turned
off (shorted).
,
• Since , the response is overdamped. Thus:
. .

101. Solution
• Given . . obtain ,
and using and :
• At :
• At :
• Find :
• Take the derivative of :
. .
• At :

102. Solution
• Given 𝐴 = −𝐴 and 5 21 − 25 𝐴 − 5 21 + 25 𝐴 = 3:
• Get 𝐴 and 𝐴 :
1 1
5 21 − 25 −5 21 − 25
𝐴
𝐴
=
0
3
• Answer:
𝐴
𝐴
=
21/70
− 21/70
=
0.0655
−0.0655
• Thus: ∴ 𝑖 𝑡 = 4 + 𝑒 − 𝑒 𝐴
• Find 𝑖 (𝑡): 𝑖 𝑡 = = = 4 + 𝑒 − 𝑒
𝑖 𝑡 =
21
70
𝑑
𝑑𝑡
𝑒 − 𝑒
𝑖 (𝑡) =
21
70
5 21 − 25
4
𝑒 +
5 21 + 25
4
𝑒
𝑖 (𝑡) =
21
56
21 − 5 𝑒 + 21 + 5 𝑒 𝑉
∴ 𝑖 (𝑡) = −0.03415𝑒 . + 0.7842𝑒 . 𝐴

103. Answers
All for .

104. Thank You!

105. 6.1 Finding Initial and Final Values
6.2 The Source-Free Series RLC Circuit
6.3 The Source-Free Parallel RLC Circuit
6.4 Step Response of a Series RLC Circuit
6.5 Step Response of a Parallel RLC Circuit
6.6 General Second-Order Circuits
6. Second-Order Circuits

106. 6.6 General Second-Order Circuits

107. Rules to Remember:
1. Determine the initial conditions and and final value
2. Turn off the independent sources and find the form of the transient response by
applying KCL and KVL.
Once a second-order differential equation is obtained, determine its characteristic roots.
Depending on whether the response is overdamped, critically damped, or underdamped, get
with two unknown constants as in the previous sections.
3. Obtain the steady-state response
4. Given that the total response is now found as the sum of the transient response and
steady-state response , determine the constants associated with the
transient response by imposing the initial conditions and found at (1).

108. Practice Problems

109. Practice
Problem
Find the complete response
and then for in the
circuit shown.

110. 1. Determine the initial and final
values
For initial values:
• At : ;
• At : ; ;
• Using KCL:
For final values at :

111. 2. Find the form of the transient
response
Turn off the independent sources:
1. Apply KCL:
2. Apply KVL:
• Substitute (1) to (2):

112. 2. Find the form of the transient
response
• Determine first then :
,
,
• Since roots are unequal and real, overdamped.

113. 2-3. Find transient response and
obtain steady-state response
• Given and :
• At :
• Thus:

114. 4. Determine the constants
associated with transient response
Given and
:
• Find A and B at :
• Take the derivative of :
• Find :

115. 4. Determine the constants
associated with transient response
• Given and :
• Get and :
• Answer:
• Thus:

116. 4. Determine the constants
associated with transient response
Given :
• Find using KCL:

117. Answers
All for

118. Practice
Problem
Find for in the
circuit shown.
A second-order circuit with two
inductors.

119. 1. Determine the initial
conditions
For initial values:
• At , 7-volt source is off. Thus:
• At , the 7-volt source is turned on but the
inductors do not change instantaneously.
• Using KVL:
For final values at :

120. 2. Find the form of the transient
response
Turn off the independent sources and apply KVL:
1. For :
2. For :
• Substitute (1) to (2):

121. 2. Find the form of the transient
response
• Determine first then :
,
,
• Since roots are unequal and real, overdamped.

122. 2-3. Find transient response and
obtain steady-state response
• Given and 10:
• At :
• Thus:

123. 4. Determine the constants
associated with transient response
Given and
:
• Find A and B at :
• Take the derivative of :
• Find :

124. 4. Determine the constants
associated with transient response
• Given and :
• Get and :
• Answer:
• Thus:

125. 4. Determine the constants
associated with transient response
Given :
• Find using KVL on :

126. Find for :
Given:
• Find :

127. Thank You!