Dokumen ini membahas konsep nilai waktu dari uang, termasuk perhitungan future value dan present value, serta aplikasi annuitas tetap dan variabel. Contoh-contoh diberikan untuk menghitung nilai uang pada masa mendatang dan nilai sekarang dari pembayaran yang akan diterima. Selain itu, terdapat penjelasan mengenai perhitungan akumulasi tabungan dan harga wajar obligasi.

1. Time Value Of Money Untuk mengetahui nilai uang yang diinvestasikan berdasarkan tingkat bunga tertentu. Untuk mengetahui berapa nilai uang secara present value dan future value. Untuk memperhitungkan sejumlah penerimaan atau pembayaran yang annuity-nya bersifat tetap. Untuk memperhitungkan sejumlah penerimaan atau pembayaran yang annuity-nya bervareasi. Syarat utama: mengetahui data tingkat bunga dan periode investasi.

2. Time Value of Money Future value (FVIF, k, n) Future value of annuity (FVIF Ann, k, n) Present value (PVIF, k, n) Present value of annuity (PVIF Ann, k, n) Khusus annuity dibedakan PMT dibayarkan di awal periode dan di akhir periode.

3. Future Value Yaitu: Besarnya nilai uang pada masa mendatang dari sejumlah uang yang diinvestasikan pada saat ini dengan tingkat bunga tertentu. Estimasi tingkat bunga berdasarkan tingkat bunga pada saat ini. Formula FV n = PV x [1 + k] n Tabel FV n = PV x [FVIF, k, n] Apalikasi pada perhitungan bunga majemuk deposito berjangka.

4. Example 1: Future Value Budi berencana akan menyimpan uangnya sebesar Rp. 1 juta, dengan tingkat bunga 20% per tahun selama 3 tahun. Pendapatan bunga selama 3 tahun tidak diambil tetapi diinvestasikan kembali. Berapa nilai uang Budi setelah jatuh tempo pada 3 tahun mendatang?

5. FV n = PV [1 + k] n FV n = Rp. 1 juta [1+ 20%] 3 FV n = Rp. 1 juta x 1,7280 = Rp. 1.728.000. Tabel FVIF (20%,3)= 1 juta x 1,7280 = 1.728.000. To T1 T2 T3 t1 Rp.1Juta Interest 20% p.a FV = ?

6. Present Value Yaitu: Besarnya nilai uang yang diterima pada saat ini dari sejumlah uang yang akan diterimakan atau jatuh tempo pada masa mendatang. Formula: Future value PV n = [1 + k] n Tabel: PV n = FV x [PVIF, k, n] Aplikasi dalam menghitung harga wajar obligasi yang berjenis zerro cupon bond.

7. Example 2: Present Value Budi akan menerima uang senilai Rp.10 juta pada 5 tahun mendatang. Uang tersebut merupakan jatuh tempo dari sekuritas yang dibeli pada saat ini. Tingkat bunga investasi 10% pada saat ini dimana suku bunga tersebut diasumsikan tetap selama 5 tahun mendatang. Berapa sebenarnya nilai sekarang atas uang Budi tersebut?.

8. Rp 10.000.000 PV n = [1 + 10%] 5 PV n = 10 juta : 1,61051 = 6.209.200 PV n = 10 juta x 1/1,61051 = 6.209.200 Tabel PVIF (10%,5) = 10 juta x 0,62092 = 6.209.200 Rp.10 Juta T0 T1 T2 T4 T5 Interest 10% p.a PV = ?

9. Future Value of Annuity Yaitu: Besarnya nilai dimasa mendatang dari penerimaan rutin yang diterima pada tahun-tahun sebelumnya, berdasarkan tingkat bunga tertentu. Annuity = PMT = sejumlah penerimaan atau pembayaran yang sifatnya rutin. [1+k] n - 1 FV Ann n = PMT x k FV Ann n = PMT x [FVIFA, k, n] Aplikasi pada perhitungan akumulatif dari tabungan

10. Example 3a: Future Value of Annuity Selama 3 tahun berturut-turut sejak tahun ini, Budi harus menabung secara rutin sebesar Rp.1 juta per tahun. Tabungan dibayarkan setiap akhir tahun dengan tingkat bunga dianggap tetap sebesar 20%. Berapa besarnya nilai akumulatif tabungan Budi setelah 3 tahun mendatang?.

11. Example 3b: Future Value of Annuity Selama 3 tahun berturut-turut sejak tahun ini, Budi harus menabung secara rutin sebesar Rp.1 juta per tahun. Tabungan dibayarkan setiap awal tahun dengan tingkat bunga dianggap tetap sebesar 20%. Berapa besarnya nilai tabungan Budi setelah 3 tahun mendatang?.

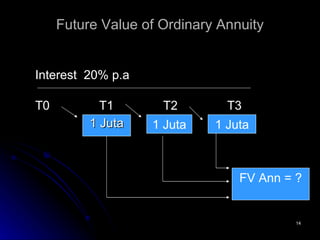
12. Payment (PMT) dibayar akhir periode [1+k] n - 1 FV Ann n = PMT x k [1+ 20%] 3 - 1 FV Ann n = 1juta x 20% FV Ann n = 1juta x 3,6400 FV Ann n = 3.640.000 Tabel FVIFA (20%,3)= 1juta x 3,6400 = 3.640.000

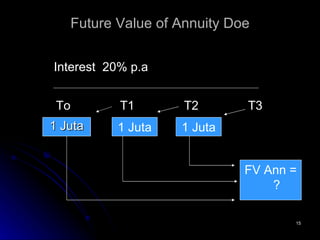
13. Payment (PMT) dibayar di awal periode [ 1+k] n - 1 FV Ann n = PMT x k x [1+k] [1+20%]3 -1 FV Ann n = 1 juta x 20% x [1+ 20%] FV Ann n = 4.368.000 Simpulan: Payment awal > akhir periode Tabel tidak dapat dipakai untuk menghitung annuity doe.

14. Future Value of Ordinary Annuity 1 Juta T0 T1 T2 T3 1 Juta 1 Juta FV Ann = ? Interest 20% p.a

15. Future Value of Annuity Doe 1 Juta To T1 T2 T3 1 Juta 1 Juta Interest 20% p.a FV Ann = ?

16. Present Value of Annuity Yaitu: Besarnya nilai sekarang atas penerimaan rutin atau pembayaran rutin yang diterima pada masa yang akan datang, dengan tingkat bunga tertentu. [1 – {1/(1+k) n }] PV Ann n = PMT x k PV Ann n = PMT x [PVIFA, k, n] Aplikasi pada perhitungan harga wajar obligasi berjenis cupon bond

17. Example 4a: Present Value of Annuity Selama 3 tahun berturut-turut sejak tahun depan, Andi menerima pembayaran bunga obligasi secara rutin sebesar Rp. 1 juta per tahun. Bunga dibayarkan setiap akhir tahun dengan tingkat bunga dianggap tetap sebesar 15%. Berapa besarnya nilai penerimaan bunga pada saat ini ?

18. Example 4b: Present Value of Annuity Selama 3 tahun berturut-turut sejak tahun depan, Andi menerima pembayaran bunga obligasi secara rutin sebesar Rp. 1 juta per tahun. Bunga dibayarkan setiap awal tahun dengan tingkat bunga dianggap tetap sebesar 15%. Berapa besarnya nilai penerimaan bunga pada saat ini ?

19. Payment (PMT) dibayar akhir periode Formula: [1 – {1/(1+15%) 3 }] PV Ann n = Rp. 1 juta x 15% PV Ann n = Rp. 1 juta x 2,2830 = Rp. 2.283.000. Tabel PVIFA (15%, 3) = 1juta x 2,2830 = 2.283.000 Tabel hanya untuk menghitung yang ordinary annuity

20. Payment (PMT) dibayar di awal periode [1 – {1/(1+k) n }] PV Ann n = PMT x k x [1+k] [1 – {1/(1+15%) 3 }] PV Ann n = 1 juta x 15% x [1+15%] PV Ann n = 2.625.450 Simpulan: Payment awal > akhir periode Tabel tidak dapat menghitung annuity doe

21. Present Value of Ordinary Annuity 1 Juta T0 T1 T2 T3 Interest 15% p.a. 1 Juta 1 Juta PV Ann = ?

22. Present Value of Annuity Doe 1 Juta T0 T1 T2 T3 Interest 15% p.a 1 Juta 1 Juta PV Ann = ?