The document outlines the process to find the transfer function of a mechanical system involving three masses and associated forces, springs, and dampers. It includes mathematical equations for each mass and provides MATLAB code for computing the transfer functions along with step and impulse responses. The conclusion highlights the differences between impulse and step responses, showcasing the system's behavior under various inputs.

1. Group:-6A 5
1
Lab:03 Transfer Function of Mechanical
Systems .
Task: For the Mechanical System Shown in Figure#1.Find the Transfer Function.
. .
Here in Figure#1
M1= M3=1kg , M2=1.5kg. K1= K2= K3=1N/m . D=0.2Ns/m.
And also find Step response and Impulse response using MATLAB.

2. Group:-6A 5
2
Solution For Task
o Mathematical Equations:- Table#1
For Mass1:-
F = M1 ̈ + k1 x1+ k2 (x1- x2)
= M1 ̈ + k1 x1+ k2x1-k2x2
= ̈ (M1) + x1(k1+ k2)- x2(k2)
For Mass3:-
0 = M3 ̈ +D ̇ + k3 (x3- x2) + k4 x3
= M3 ̈ +D ̇ + k3 x3- k3 x2+ k4 x3
= ̈ (M3) +D ̇ + x3(k3+ k4)- x2(k3)
For Mass2:-
0 = M2 ̈ + k2 (x2- x1) + k3 (x2- x3)
= M2 ̈ + k2 x2- k2 x1+ k3 x2- k3 x3
= ̈ (M2) + x2(k2+ k3)- x1(k2)- x3(k3)
o Transfer Function Equations:- Table#2
For Mass1:-
F = X1(s)[ M1s2
+ k1+ k2]- X2(s)[ k2]
For Mass3:-
0 = -X2(s)[ k3]+ X3(s)[ M3s2
+Ds + k3+ k4]
For Mass2:-
0 = -X1(s)[ k2]+ X2(s)[ M2s2
+ k2+ k3]
- X3(s)[ k3]
 Putting values of Mases ,Springs and Damper given in Eq(1), Eq(2), Eq(3).
F = X1(s)[ s2
+ 2]- X2(s)+0 --------------------------Eq(1)
0 = -X1(s)+ X2(s)[1.5s2
+2] - X3(s) --------------------------Eq(2)
0 = 0-X2(s)+ X3(s)[s2
+0.2s+2] --------------------------Eq(3)
o In Matrix Form in MATLAB
[ s^2 + 2, -1, 0]
[ -1, (3*s^2)/2 + 2, -1]
[ 0, -1, s^2 + s/5 + 2]

3. Group:-6A 5
3
o Code of Task In MATLAB
syms s F X x1 x2 x3 f
X=[x1; x2; x3]
F=[f; 0; 0]
z=[s^2+2 -1 0; -1 1.5*s^2+2 -1; 0 -1 s^2+0.2*s+2]
ZIN=inv(z)
X=ZIN*F
x1=X(1)/f
x2=X(2)/f
x3=X(3)/f
[n1,d1]=numden(x1)
[n2,d2]=numden(x2)
[n3,d3]=numden(x3)
num1=sym2poly(n1);
num2=sym2poly(n2);
num3=sym2poly(n3);
den1=sym2poly(d1);
den2=sym2poly(d2);
den3=sym2poly(d3);
g1=tf(num1,den1);
g2=tf(num2,den2);
g3=tf(num3,den3);
figure
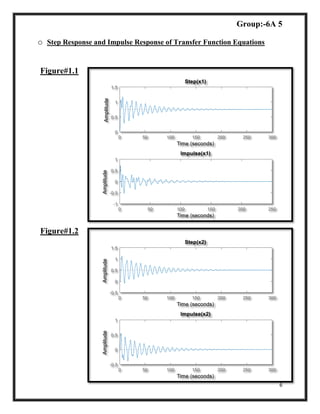
subplot(2,1,1)
step(g1)
title('Step(x1)')
subplot(2,1,2)
impulse(g1)
title('Impulse(x1)')
figure
subplot(2,1,1)
step(g2)
title('Step(x2)')
subplot(2,1,2)
impulse(g2)
title('Impulse(x2)')

4. Group:-6A 5
4
figure
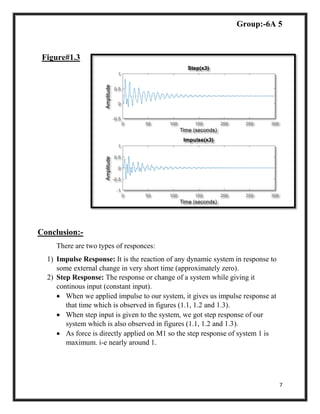
subplot(2,1,1)
step(g3)
title('Step(x3)')
subplot(2,1,2)
impulse(g3)
title('Impulse(x3)')
o Code Result In Command Window
X =
x1
x2
x3
F =
f
0
0
z =
[ s^2 + 2, -1, 0]
[ -1, (3*s^2)/2 + 2, -1]
[ 0, -1, s^2 + s/5 + 2]
ZIN =
[ (15*s^4 + 3*s^3 + 50*s^2 + 4*s + 30)/(15*s^6 + 3*s^5 + 80*s^4 + 10*s^3 + 120*s^2 + 6*s
+ 40), (2*(5*s^2 + s + 10))/(15*s^6 + 3*s^5 + 80*s^4 + 10*s^3 + 120*s^2 + 6*s + 40),
10/(15*s^6 + 3*s^5 + 80*s^4 + 10*s^3 + 120*s^2 + 6*s + 40)]
[ (2*(5*s^2 + s + 10))/(15*s^6 + 3*s^5 + 80*s^4 + 10*s^3 + 120*s^2 + 6*s + 40), (2*(s^2 +
2)*(5*s^2 + s + 10))/(15*s^6 + 3*s^5 + 80*s^4 + 10*s^3 + 120*s^2 + 6*s + 40),
(10*(s^2 + 2))/(15*s^6 + 3*s^5 + 80*s^4 + 10*s^3 + 120*s^2 + 6*s + 40)]
[10/(15*s^6 + 3*s^5 + 80*s^4 + 10*s^3 + 120*s^2 + 6*s + 40), (10*(s^2 +
2))/(15*s^6 + 3*s^5 + 80*s^4 + 10*s^3 + 120*s^2 + 6*s + 40), (5*(3*s^4 + 10*s^2 +
6))/(15*s^6 + 3*s^5 + 80*s^4 + 10*s^3 + 120*s^2 + 6*s + 40)]
X =
(f*(15*s^4 + 3*s^3 + 50*s^2 + 4*s + 30))/(15*s^6 + 3*s^5 + 80*s^4 + 10*s^3 + 120*s^2 +
6*s + 40) (2*f*(5*s^2 + s + 10))/(15*s^6 + 3*s^5 + 80*s^4 + 10*s^3 + 120*s^2 + 6*s + 40)
(10*f)/(15*s^6 + 3*s^5 + 80*s^4 + 10*s^3 + 120*s^2 + 6*s + 40)

5. Group:-6A 5
5
 Transfer Function Equations x1,x2,x3
x1 =
(15*s^4 + 3*s^3 + 50*s^2 + 4*s + 30)/(15*s^6 + 3*s^5 + 80*s^4 + 10*s^3 + 120*s^2 + 6*s +
40)
x2 =
(2*(5*s^2 + s + 10))/(15*s^6 + 3*s^5 + 80*s^4 + 10*s^3 + 120*s^2 + 6*s + 40)
x3 =
10/(15*s^6 + 3*s^5 + 80*s^4 + 10*s^3 + 120*s^2 + 6*s + 40)
 Numenators and Denominators of Tarnsfer Equation x1,x2,x3
n1 =
15*s^4 + 3*s^3 + 50*s^2 + 4*s + 30
d1 =
15*s^6 + 3*s^5 + 80*s^4 + 10*s^3 + 120*s^2 + 6*s + 40
n2 =
10*s^2 + 2*s + 20
d2 =
15*s^6 + 3*s^5 + 80*s^4 + 10*s^3 + 120*s^2 + 6*s + 40
n3 =
10
d3 =
15*s^6 + 3*s^5 + 80*s^4 + 10*s^3 + 120*s^2 + 6*s + 40

6. Group:-6A 5
6
o Step Response and Impulse Response of Transfer Function Equations
Figure#1.1
Figure#1.2

7. Group:-6A 5
7
Figure#1.3
Conclusion:-
There are two types of responces:
1) Impulse Response: It is the reaction of any dynamic system in response to
some external change in very short time (approximately zero).
2) Step Response: The response or change of a system while giving it
continous input (constant input).
 When we applied impulse to our system, it gives us impulse response at
that time which is observed in figures (1.1, 1.2 and 1.3).
 When step input is given to the system, we got step response of our
system which is also observed in figures (1.1, 1.2 and 1.3).
 As force is directly applied on M1 so the step response of system 1 is
maximum. i-e nearly around 1.