1) The document describes a digital signal processing lab report that analyzes Gibbs phenomenon using different sinc functions to design filters. 2) The lab uses sinc functions with varying indices to design low-pass, high-pass, band-pass and band-stop filters. The effect of the sinc function length on frequency response and Gibbs phenomenon is observed. 3) Gibbs phenomenon occurs near discontinuities, where the Fourier series approximation will always have an error in the form of an overshoot near the discontinuity, about 9% of the size of the jump, no matter how many terms are used.

1. Digital Signal
Processing
Lab report 09
Submitted By:
Syed Abuzar
Reg Number:
SP15-BEE-096
Submitted To:
Sir Usman
BEE-5A
Date: 12/06/2017

2. Filter Design and Gibb’s Phenomenon
Objective:
In today’s Lab we will use different versions of
sinc function to design Low-pass, High-pass,
Band-pass, and band-stop filters. We will also
analyze the effect of length of h[n] on frequency
response and understand Gibb’s phenomenon.
Procedure:
1. Open M-file or M-Book
2. Save it by any useful name but remember not to
start the name by any numeric digit, do not use
any special character other than under-the-score
( _ ) and also remember not to give any space in
the name.
Gibb’s phenomenon occurs near a jump
discontinuity in the signal. It says that no
matter how many terms you include in your Fourier
series there will always be an error in the form
of an overshoot near the discontinuity. The
overshoot always be about 9% of the size of the
jump.
Task I:
3. Generate a sinc function with a zero crossing
frequency of 100 Hz and simulated sampling
frequency of 2500 Hz keeping index n=-100:100.
4. Analyze the Fourier transform of the signal
from step one using code from Lab2.
5. Now change the length of index to n=-200:200
and later to n=-1000:1000. While changing the
length continuously observe the effect on
magnitude of fft.

3. 6. You can also observe the wrapped and unwrapped
phase of the sinc function using angle and phase
command, respectively.
7. For calculating group delay take negative
derivative of the unwrapped phase, which shall be
approximate to 0.
 Matlab Code:
 Index =-100:100:

clc
close all
clear all
%Index
n=input('Index = ');
%Zero Crossing frequency
fc=input('Zero Crossing Frequency =');
%simulated frequency
fs=input('Simulated Frequency = ');
%size
N=input('Size in fourier transform = ');
%sinc function
h=sinc(2*fc/fs*n);
%plot the sinc function
subplot(221);
plot(n,h);
title('h_[n]');
grid on
ylabel 'Amplitude'
xlabel 'T(msec)'
%Omega Axis
w=linspace(-fs/2,fs/2,N);
%fourier transform
H=fftshift(fft(h,N));
%plot of Magnitude
subplot(222);
plot(w,abs(H));
title 'Magnitude of fourier transform'
ylabel 'Amplitude'
xlabel 'W rad/sec'
%plot Phase response
subplot(223);
plot(w,angle(H));

4. title 'Phase Response'
ylabel 'Amplitude'
xlabel 'w rad/sec'
%plot group delay
subplot(224);
plot(w(1:4999),-diff(phase(H)));
title 'Phase Response of group delay'
ylabel 'Amplitude'
xlabel 'w rad/sec'
Output:
 Index= -100:100:
o Input Command Window:
Simulated frequency and size of fourier
transform.
Index is taken as -100:100.
o Graph:

5. In the above output, we see that when the index
is -100:100 then the there is little jumps in the
sinc function fourier transform
 Index -1000:1000:
o Input Command Window:
o Graph:

6. In the above graph, index is given as -1000:1000
and then there is a more error in the distortion
nut there are ignore because more term are added
then the gibb’s phenomenon is understand.
 Index -200:200:
o Input Command Window:
o Graph:

7. In the above graph we clearly see that the jump
near the discontinuity is that when the more term
are accommodated in the fourier transform then
there will be error never the over shoot.
Task II:
8. Now multiply with the sinc function and
repeat step 4 to 7.
9. Now multiply (where fs/2 can be
mapped to π) with the sinc function and repeat
step 4 to 7.
10. Add signals from step 3 and 8, forming a new
impulse response and repeat step 4 to 7.
Multiply :
 Matlab Code:
clc
close all
clear all
%Index
n=input('Index = ');
%Zero Crossing frequency
fc=input('Zero Crossing Frequency =');

8. %simulated frequency
fs=input('Simulated Frequency = ');
%size
N=input('Size in fourier transform = ');
%sinc function
h=sinc(2*fc/fs*n).*exp(-1i*pi*n);
%plot the sinc function
subplot(221);
plot(n,h);
title('h[n]');
grid on
ylabel 'Amplitude'
xlabel 'T(msec)'
%Omega Axis
w=linspace(-fs/2,fs/2,N);
%fourier transform
H=fftshift(fft(h,N));
%plot of Magnitude
subplot(222);
plot(w,abs(H));
title 'Magnitude of fourier transform'
ylabel 'Amplitude'
xlabel 'W rad/sec'
%plot Phase response
subplot(223);
plot(w,angle(H));
title 'Phase Response'
ylabel 'Amplitude'
xlabel 'w rad/sec'
%plot group delay
subplot(224);
plot(w(1:4999),-diff(phase(H)));
title 'Phase Response of group delay'
ylabel 'Amplitude'
xlabel 'w rad/sec'
Output:
 Index =-100:100:
o Input Comand Window:

9. o Graph:
In the above graph, we take the index as -100:100
then the transform is shifted to the pi & it is
repeated on the pi and –pi.
 Index =-200:200:
o Graph:

10. In the above graph ,we take more term in as
increases the index mean by choosing -200:200 and
then repeated the sinc function transform along
pi and –pi .
 Index =-1000:1000:
o Graph:
In this graph, we take index -1000:1000 mean
more term are includes in it means that

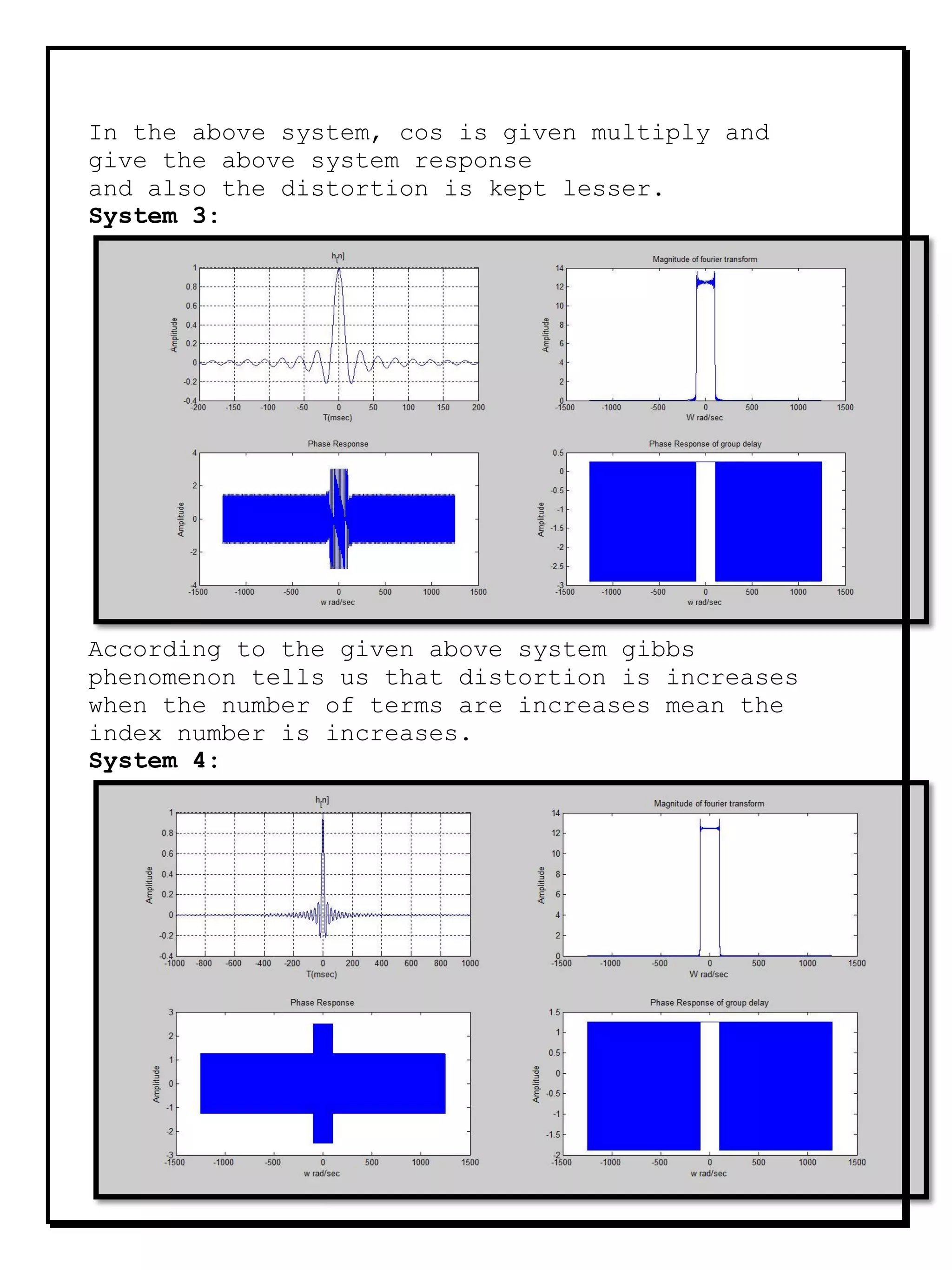
11. exponential is shifting in the fourier transform
and more jums are occur and error are increasing.
Multiply Cos(2*pi/2*n):
 Matlab Code:
clc
close all
clear all
%Index
n=input('Index = ');
%Zero Crossing frequency
fc=input('Zero Crossing Frequency =');
%simulated frequency
fs=input('Simulated Frequency = ');
%size
N=input('Size in fourier transform = ');
%sinc function
h=sinc(2*fc/fs*n).*cos(2*(pi/2)*n);
%plot the sinc function
subplot(221);
plot(n,h);
title('h[n]');
grid on
ylabel 'Amplitude'
xlabel 'T(msec)'
%Omega Axis
w=linspace(-fs/2,fs/2,N);
%fourier transform
H=fftshift(fft(h,N));
%plot of Magnitude
subplot(222);
plot(w,abs(H));
title 'Magnitude of fourier transform'
ylabel 'Amplitude'
xlabel 'W rad/sec'
%plot Phase response
subplot(223);
plot(w,angle(H));
title 'Phase Response'
ylabel 'Amplitude'
xlabel 'w rad/sec'
%plot group delay
subplot(224);
plot(w(1:4999),-diff(phase(H)));
title 'Phase Response of group delay'
ylabel 'Amplitude'
xlabel 'w rad/sec'

12. Output:
 Graph:
o Index -100:100:
In the above graph, the fourier is similar to
that of the exponential shift and also the
distortion is increases.
 Index -200:200:
o Graph:

13. In the above graph, Gibb’s Phenomenon is tell
that when the term or the index number is
increases then the distortion is also increases.
 Index =-1000:1000:
o Graph:
In the above graph, when the index is increases
to -1000:1000 then distortion is also increases
mean the following filter will be the clearly
established.

14. Question and Answers:
Q.No.01:
If all above four versions of sinc act as impulse
response of a system describe a detail of all
four systems.
Answer:
In the given below the impulse response of the
four system are described as
System 1:
In the above system response we take index -
100:100 then there is less distortion and as the
number of index is increasing then the distortion
is also increasing.
System 2:

15. In the above system, cos is given multiply and
give the above system response
and also the distortion is kept lesser.
System 3:
According to the given above system gibbs
phenomenon tells us that distortion is increases
when the number of terms are increases mean the
index number is increases.
System 4:

16. In the above graph, it is clearly shown that when
the number of terms are increases when the index
number is increases.
Q.No.02:
If a shift of n0 is given in the sinc function
what will be the effect on group delay? Provide
justification of your answer with the help of
plots.
Answer:
In the above graph ,it is clearly observe that
when the exponential is multiply with that of the
sinc function is basically shifted the given
fourier transform to that of it repeatedly on the
pi to –pi.
Q.No.03:
What do you understand by Gibb’s phenomenon?
Answer:
The given group delay responses of the given
phase is given as

17. In the given above different types of the
magnitude responses is given that Gibb’s
Phenomenon means that when the number of term is
increases then the error is increases when the
jump of the distortion is producing the
discontinuity.
Conclusion:
In this lab,I learnt about the gibb’s phenomenon
and also means that increasing the number of
term is increasing the errors and also the jumps
discontinuity which increases the errors.