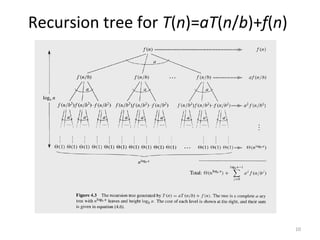
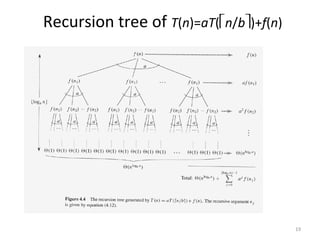
The document discusses recurrences and the master theorem for finding asymptotic bounds of recursive equations. It covers the substitution method, recursive tree method, and master theorem. The master theorem provides bounds for recurrences of the form T(n) = aT(n/b) + f(n) based on comparing f(n) to nlogba. It also discusses exceptions, gaps in the theorem, and proofs of the main results.

1. 1
Asymptotic Efficiency of Recurrences
• Find the asymptotic bounds of recursive equations.
– Substitution method
• domain transformation
• Changing variable
– Recursive tree method
– Master method (master theorem)
• Provides bounds for: T(n) = aT(n/b)+f(n) where
– a ≥ 1 (the number of subproblems).
– b>1, (n/b is the size of each subproblem).
– f(n) is a given function.

2. 2
Recurrences
• MERGE-SORT
– Contains details:
• T(n) = Θ(1) if n=1
T(n/2)+ T(n/2)+ Θ(n) if n>1
• Ignore details, T(n) = 2T(n/2)+ Θ(n).
– T(n) = Θ(1) if n=1
2T(n/2)+ Θ(n) if n>1

3. 3
Master Method/Theorem
• Theorem 4.1 (page 73)
– for T(n) = aT(n/b)+f(n), n/b may be n/b or n/b.
– where a ≥ 1, b>1 are positive integers, f(n) be a non-
negative function.
1. If f(n)=O(nlogb
a-ε) for some ε>0, then T(n)= Θ(nlogb
a
).
2. If f(n)= Θ(nlogb
a
), then T(n)= Θ(nlogb
a
lg n).
3. If f(n)=Ω(nlogb
a+ε) for some ε>0, and if af(n/b) ≤cf(n) for
some c<1 and all sufficiently large n, then T(n)=
Θ(f(n)).

4. 4
Implications of Master Theorem
• Comparison between f(n) and nlogb
a
(<,=,>)
• Must be asymptotically smaller (or larger) by a
polynomial, i.e., nε
for some ε>0.
• In case 3, the “regularity” must be satisfied, i.e.,
af(n/b) ≤cf(n) for some c<1 .
• There are gaps
– between 1 and 2: f(n) is smaller than nlogb
a
, but not
polynomially smaller.
– between 2 and 3: f(n) is larger than nlogb
a
, but not
polynomially larger.
– in case 3, if the “regularity” fails to hold.

5. 5
Application of Master Theorem
• T(n) = 9T(n/3)+n;
– a=9,b=3, f(n) =n
– nlogb
a
= nlog3
9
= Θ (n2
)
– f(n)=O(nlog3
9-ε) for ε=1
– By case 1, T(n) =Θ (n2
).
• T(n) = T(2n/3)+1
– a=1,b=3/2, f(n) =1
– nlogb
a
= nlog3/2
1
= Θ (n0
) = Θ (1)
– By case 2, T(n)= Θ(lg n).

6. 6
Application of Master Theorem
• T(n) = 3T(n/4)+nlg n;
– a=3,b=4, f(n) =nlg n
– nlogb
a
= nlog4
3
= Θ (n0.793
)
– f(n)= Ω(nlog4
3+ε) for ε≈0.2
– Moreover, for large n, the “regularity” holds for
c=3/4.
• af(n/b) =3(n/4)lg (n/4) ≤ (3/4)nlg n = cf(n)
– By case 3, T(n) =Θ (f(n))=Θ (nlg n).

7. 7
Exception to Master Theorem
• T(n) = 2T(n/2)+nlg n;
– a=2,b=2, f(n) =nlg n
– nlogb
a
= nlog2
2
= Θ (n)
– f(n) is asymptotically larger than nlogb
a
, but not
polynomially larger because
– f(n)/nlogb
a
= lg n, which is asymptotically less than nε
for any ε>0.
– Therefore,this is a gap between 2 and 3.

8. 8
Where Are the Gaps
nlogba f(n), case 2: within constant distances
c1
c2
nε
f(n), case 1, at least polynomially smaller
Gap between case 1 and 2
nε
Gap between case 3 and 2
f(n), case 3, at least polynomially larger
Note: 1. for case 3, the regularity also must hold.
2. if f(n) is lg n smaller, then fall in gap in 1 and 2
3. if f(n) is lg n larger, then fall in gap in 3 and 2
4. if f(n)=Θ(nlogba
lgk
n), then T(n)=Θ(nlogba
lgk+1
n). (as exercise)

9. 9
Proof of Master Theorem
• The proof for the exact powers, n=bk
for k≥1.
• Lemma 4.2
– for T(n) = Θ(1) if n=1
– aT(n/b)+f(n) if n=bk
for k≥1
– where a ≥ 1, b>1, f(n) be a nonnegative function,
– Then
– T(n) = Θ(nlogba
)+ aj
f(n/bj
)
• Proof:
– By iterating the recurrence
– By recursion tree (See figure 4.3)
∑
j=0
logb
n-1

10. 10
Recursion tree for T(n)=aT(n/b)+f(n)

11. 11
Proof of Master Theorem (cont.)
• Lemma 4.3:
– Let a ≥ 1, b>1, f(n) be a nonnegative function defined on
exact power of b, then
– g(n)= aj
f(n/bj
) can be bounded for exact power of b as:
1. If f(n)=O(nlogb
a-ε) for some ε>0, then g(n)= O(nlogb
a
).
2. If f(n)= Θ(nlogb
a
), then g(n)= Θ(nlogb
a
lg n).
3. If f(n)= Ω(nlogb
a+ε) for some ε>0 and if af(n/b) ≤cf(n) for some
c<1 and all sufficiently large n ≥b, then g(n)= Θ(f(n)).
∑
j=0
logb
n-1

12. 12
Proof of Lemma 4.3
• For case 1: f(n)=O(nlogb
a-ε) implies f(n/bj
)=O((n /bj
)logb
a-ε), so
• g(n)= aj
f(n/bj
) =O( aj
(n /bj
)logb
a-ε)
• = O(nlogb
a-ε aj
/(blogb
a-ε)j
) = O(nlogb
a-ε aj
/(aj
(b-ε)j
))
• = O(nlogb
a-ε (bε)j
) = O(nlogb
a-ε(((bε)logbn
-1)/(bε
-1) )
• = O(nlogb
a-ε(((blogbn
)ε
-1)/(bε
-1)))=O(nlogb
a
n-ε
(nε
-1)/(bε
-1))
• = O(nlogb
a
)
∑
j=0
logb
n-1
∑
j=0
logb
n-1
∑
j=0
logb
n-1
∑
j=0
logb
n-1
∑
j=0
logb
n-1

13. 13
Proof of Lemma 4.3(cont.)
• For case 2: f(n)= Θ(nlogb
a
) implies f(n/bj
)= Θ((n /bj
)logb
a
), so
• g(n)= aj
f(n/bj
) = Θ( aj
(n /bj
)logb
a
)
• = Θ(nlogb
a
aj
/(blogb
a
)j
) = Θ(nlogb
a
1)
• = Θ(nlogb
a
logb
n) = Θ(nlogb
a
lg n)
∑
j=0
logb
n-1
∑
j=0
logb
n-1
∑
j=0
logb
n-1
∑
j=0
logb
n-1

14. 14
Proof of Lemma 4.3(cont.)
• For case 3:
– Since g(n) contains f(n), g(n) = Ω(f(n))
– Since af(n/b) ≤cf(n), aj
f(n/bj
) ≤cj
f(n) , why???
– g(n)= aj
f(n/bj
) ≤ cj
f(n) ≤ f(n) cj
– =f(n)(1/(1-c)) =O(f(n))
– Thus, g(n)=Θ(f(n))
∑
j=0
logb
n-1
∑
j=0
logb
n-1
∑
j=0
∞

15. 15
Proof of Master Theorem (cont.)
• Lemma 4.4:
– for T(n) = Θ(1) if n=1
– aT(n/b)+f(n) if n=bk
for k≥1
– where a ≥ 1, b>1, f(n) be a nonnegative function,
1. If f(n)=O(nlogb
a-ε) for some ε>0, then T(n)= Θ(nlogb
a
).
2. If f(n)= Θ(nlogb
a
), then T(n)= Θ(nlogb
a
lg n).
3. If f(n)=Ω(nlogb
a+ε) for some ε>0, and if af(n/b) ≤cf(n) for
some c<1 and all sufficiently large n, then T(n)=
Θ(f(n)).

16. 16
Proof of Lemma 4.4 (cont.)
• Combine Lemma 4.2 and 4.3,
– For case 1:
• T(n)= Θ(nlogb
a
)+O(nlogb
a
)=Θ(nlogb
a
).
– For case 2:
• T(n)= Θ(nlogb
a
)+Θ(nlogb
a
lg n)=Θ(nlogb
a
lg n).
– For case 3:
• T(n)= Θ(nlogb
a
)+Θ(f(n))=Θ(f(n)) because f(n)= Ω(nlogb
a+ε).

17. 17
Floors and Ceilings
• T(n)=aT(n/b)+f(n) and T(n)=aT(n/b)+f(n)
• Want to prove both equal to T(n)=aT(n/b)+f(n)
• Two results:
– Master theorem applied to all integers n.
– Floors and ceilings do not change the result.
• (Note: we proved this by domain transformation too).
• Since n/b≤n/b, and n/b≥ n/b, upper bound for
floors and lower bound for ceiling is held.
• So prove upper bound for ceilings (similar for lower
bound for floors).

18. 18
Upper bound of proof for T(n)=aT(n/b)+f(n)
• consider sequence n, n/b,  n/b/b,   n/b /b/b,
…
• Let us define nj as follows:
• nj= n if j=0
• = nj-1/b if j>0
• The sequence will be n0, n1, …, nlogb
n
• Draw recursion tree:

19. 19
Recursion tree of T(n)=aT(n/b)+f(n)

20. 20
The proof of upper bound for ceiling
– T(n) = Θ(nlogba
)+ aj
f(nj)
– Thus similar to Lemma 4.3 and 4.4, the upper
bound is proven.
∑
j=0
logb
n -1

21. 21
The simple format of master theorem
• T(n)=aT(n/b)+cnk
, with a, b, c, k are positive
constants, and a≥1 and b≥2,
O(nlogba
), if a>bk
.
• T(n) = O(nk
logn), if a=bk
.
O(nk
), if a<bk
.

22. 22
Summary
Recurrences and their bounds
– Substitution
– Recursion tree
– Master theorem.
– Proof of subtleties
– Recurrences that Master theorem does not
apply to.