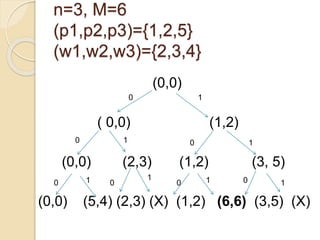
The document discusses the 0/1 knapsack problem and the greedy algorithm approach. It describes the knapsack problem as selecting a subset of items with weights and values that fit within a knapsack capacity while maximizing the total value. The greedy algorithm works by selecting the highest value item at each step that fits within remaining capacity. The document provides an example problem of selecting boxes to fill a knapsack of 15kg capacity to maximize profit. It outlines the recurrence relation and time/space complexity of the greedy knapsack algorithm.

1. 0/1 KNAPSACK PROBLEM
CH.KARTHIK
13MSN0083
VIT UNIVERSITY

2. Greedy Method
 It is a design technique applied to those
problems having n inputs and requires us
to obtain a subset that satisfies some
constraints.
 Any subset that satisfies these constraints
is called a feasible solution.
Ultimate goal is to find a feasible solution
that minimizes [or maximizes] an
objective function; this solution is known
as optimal solution.

3. // Algorithm takes as input an array a of n
elements
algorithm greedy ( a, n )
{
solution = {}; // Initially empty
for ( i = 0; i < n; i++ )
{
// Select an input from a and remove it from
further consideration
x = select ( a );
if ( feasible ( solution, x ) )
solution = solution + x; // Union
}
return ( solution );
}

4. Knapsack
 A 1998 study of the Stony Brook
University Algorithm Repository showed
that, out of 75 algorithmic problems, the
knapsack problem was the 18th most
popular and the 4th most needed after kd-trees,
suffix trees, and the bin packing
problem

5. Knapsack problem
 Given a set of items, each with a mass
and a value, determine the number of each
item to include in a collection so that the
total weight is less than or equal to a given
limit and the total value is as large as
possible.
 It derives its name from the problem
faced by someone who is constrained by a
fixed-size knapsack and must fill it with
the most valuable items.

6. which boxes should be chosen to maximize
the amount of money while still keeping
the overall weight under or equal to 15 kg?

7.  Answer: 3 yellow boxes and 3 grey boxes .
 To get maximum profit, such that weight in the
knapsack do not exceed its capacity.
 Given ‘n’ objects and a knapsack(bag).
 Object i have a weight Wi, and the knapsack
has a capacity m.
 if object i is placed into knapsack then a profit
of Pi is earned.
 since the knapsack capacity is m, we require
the total weight of all chosen objects to be at
most m.

8.  Σ Wi xi > m { problem arises here}
 Σ Wi xi ≤ m {item placed such that not
to exceed the weight of bag}
 let fn(m) represents the profit obtained
with ‘n’ objects
Fn(m)=max{Pn+fn-1(m-wn) / 0+fn-1(m)}
this is recurrence relation.
 Time complexity is O(n maxw).
 Space complexity is O(n maxw).

9. n=3, M=6
(p1,p2,p3)={1,2,5}
(w1,w2,w3)={2,3,4}
(0,0)
0 1
( 0,0) (1,2)
0
1
0 1
(0,0) (2,3) (1,2) (3, 5)
0
1
1 0 0 1 0 1
(0,0) (5,4) (2,3) (X) (1,2) (6,6) (3,5) (X)

10. Than’Q’
