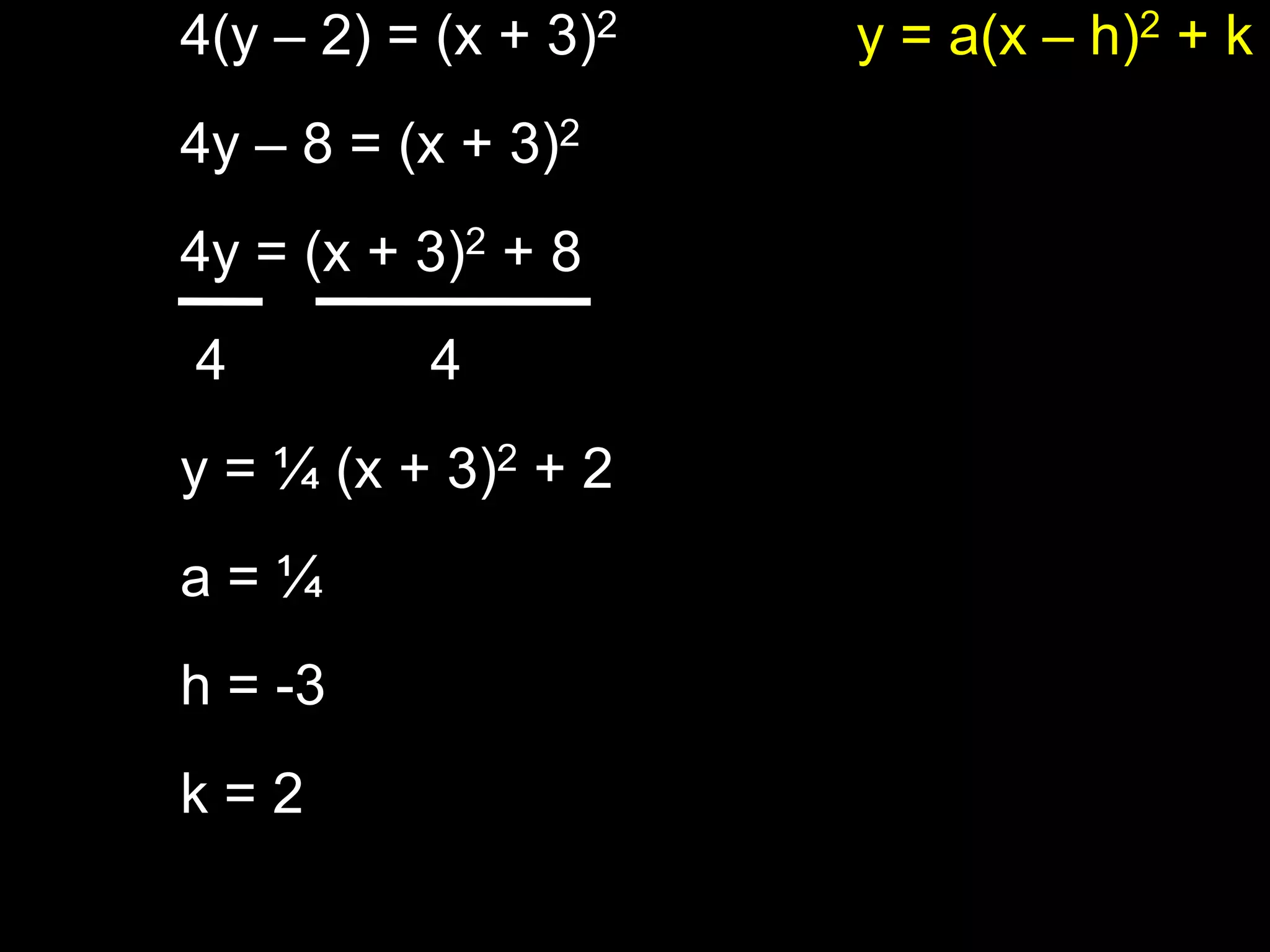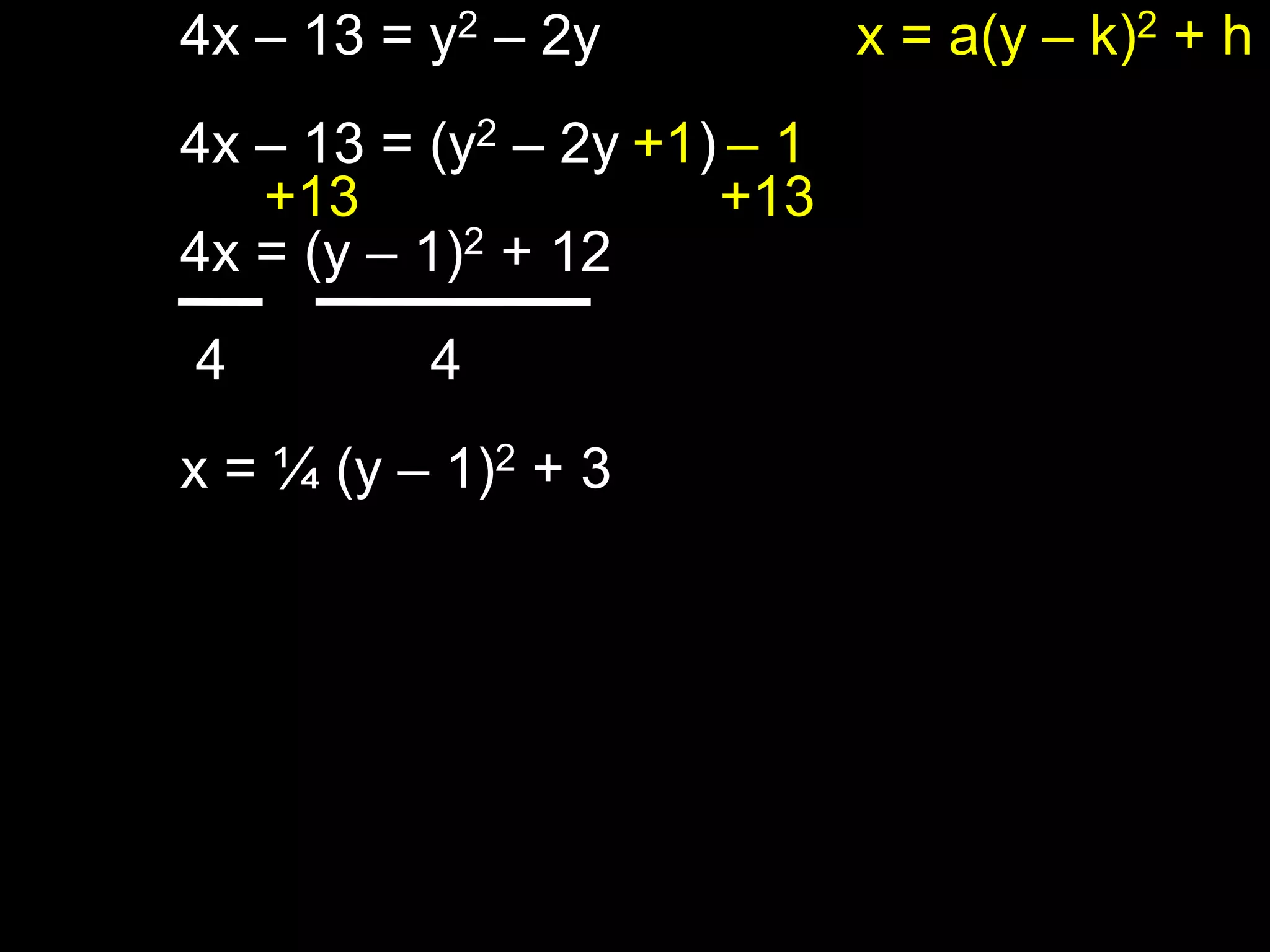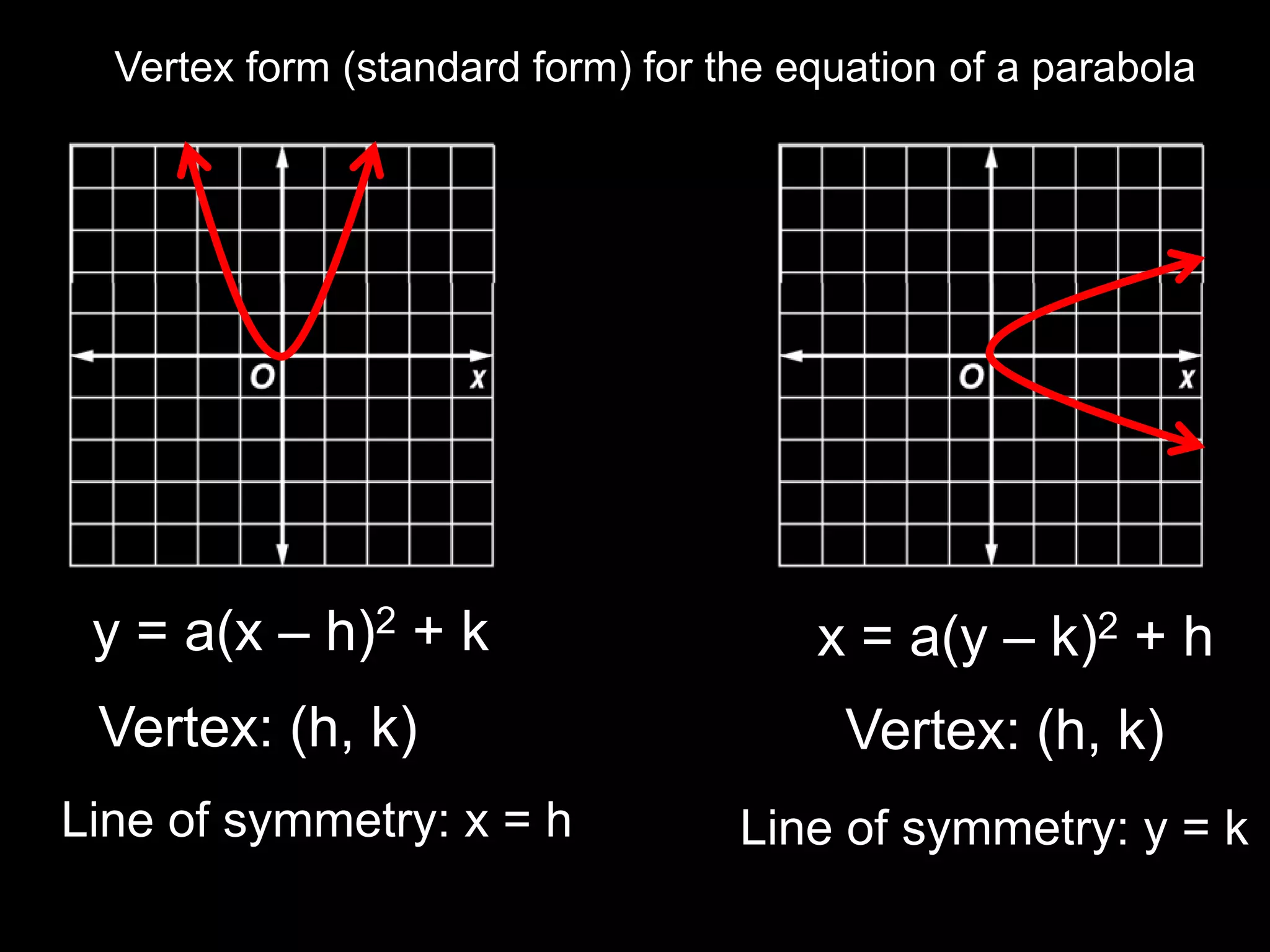
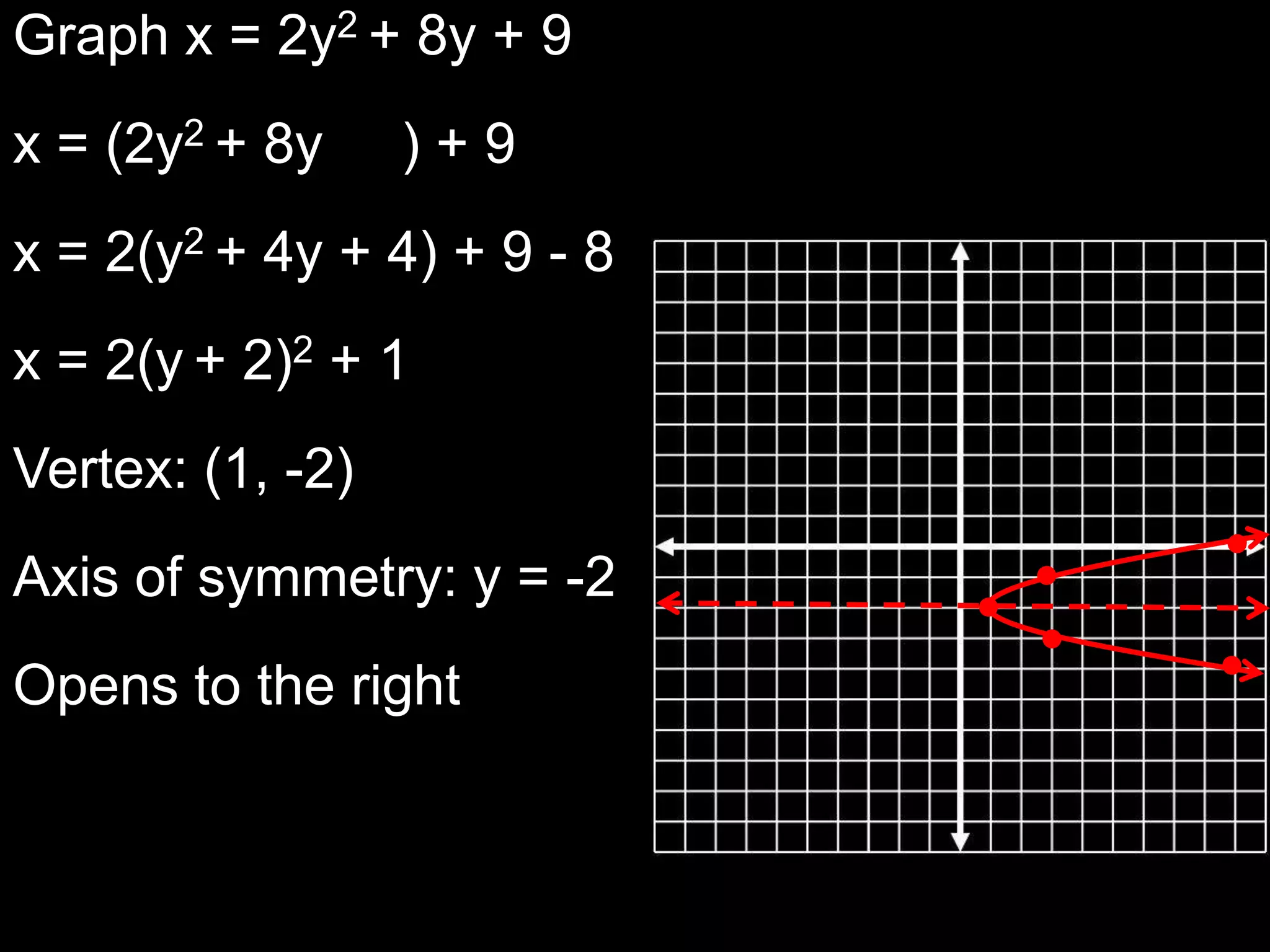
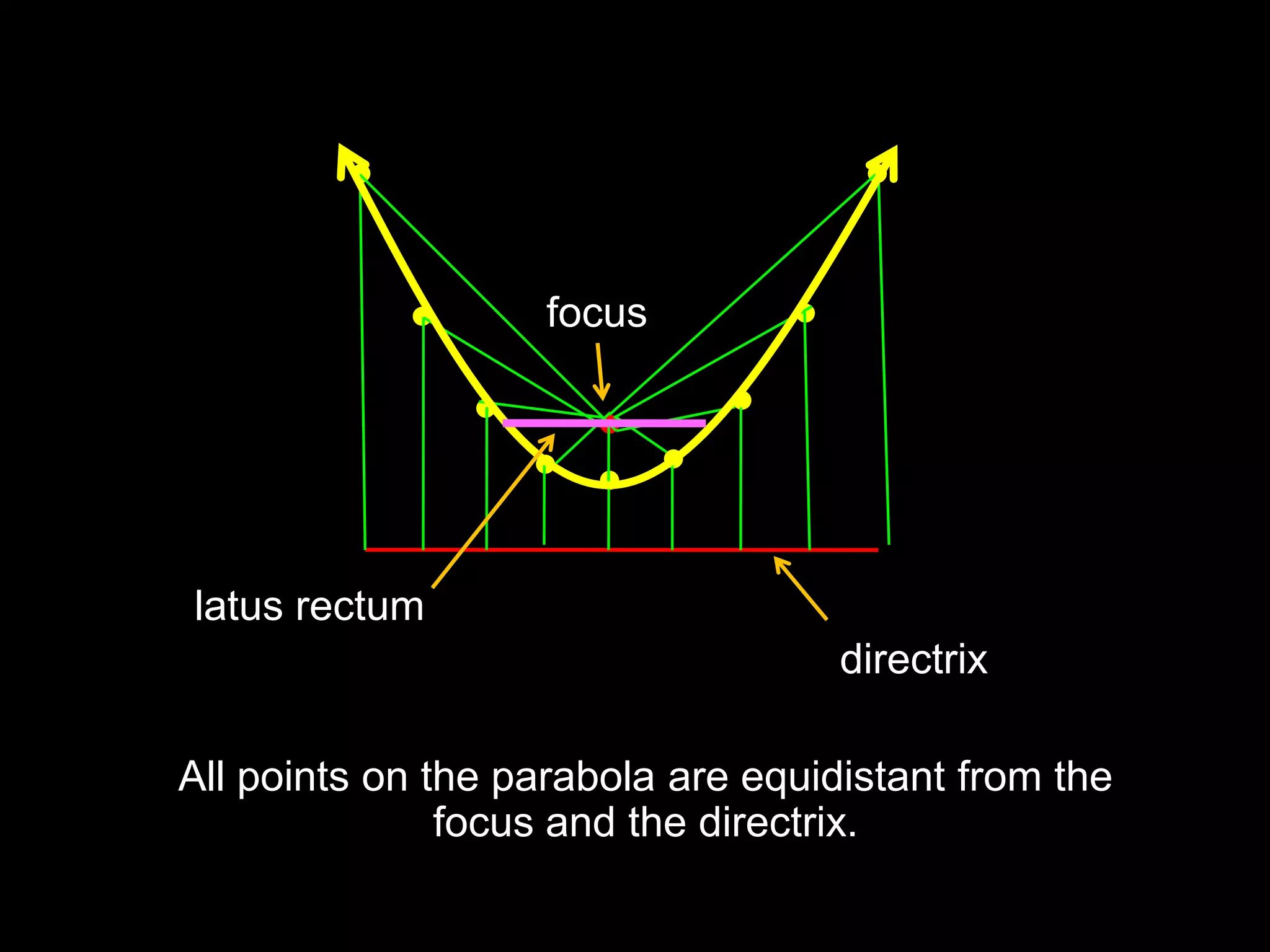
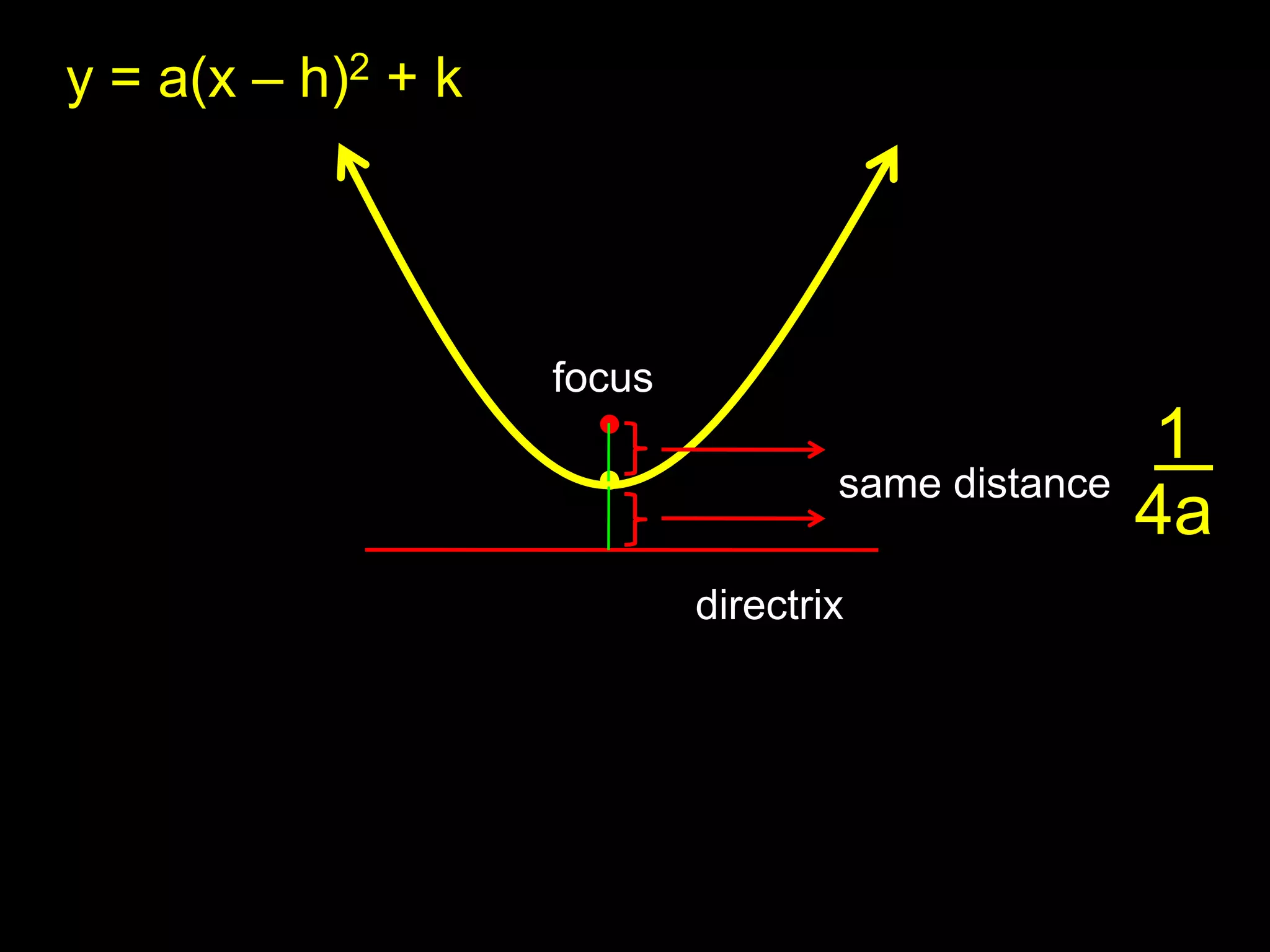
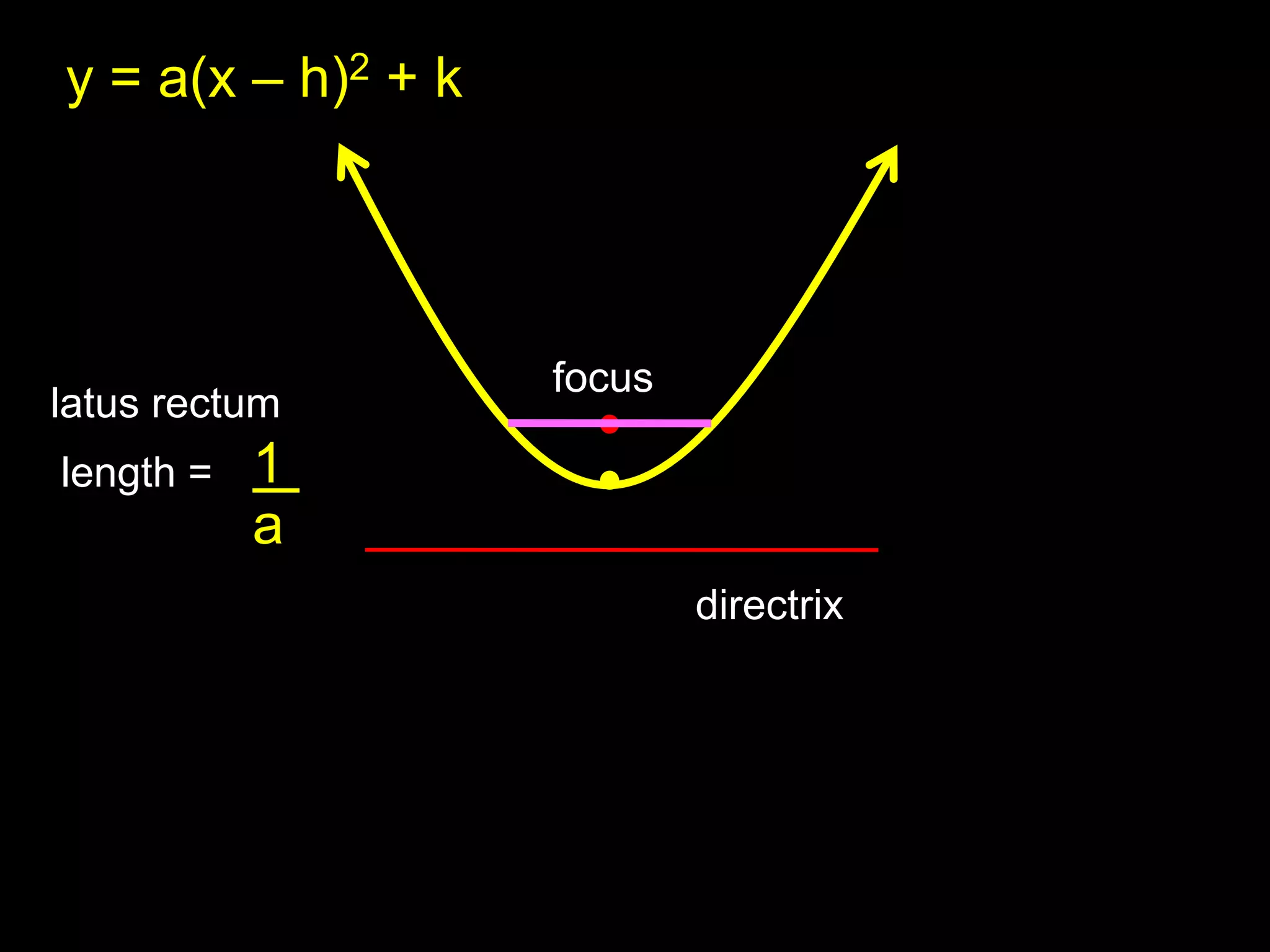
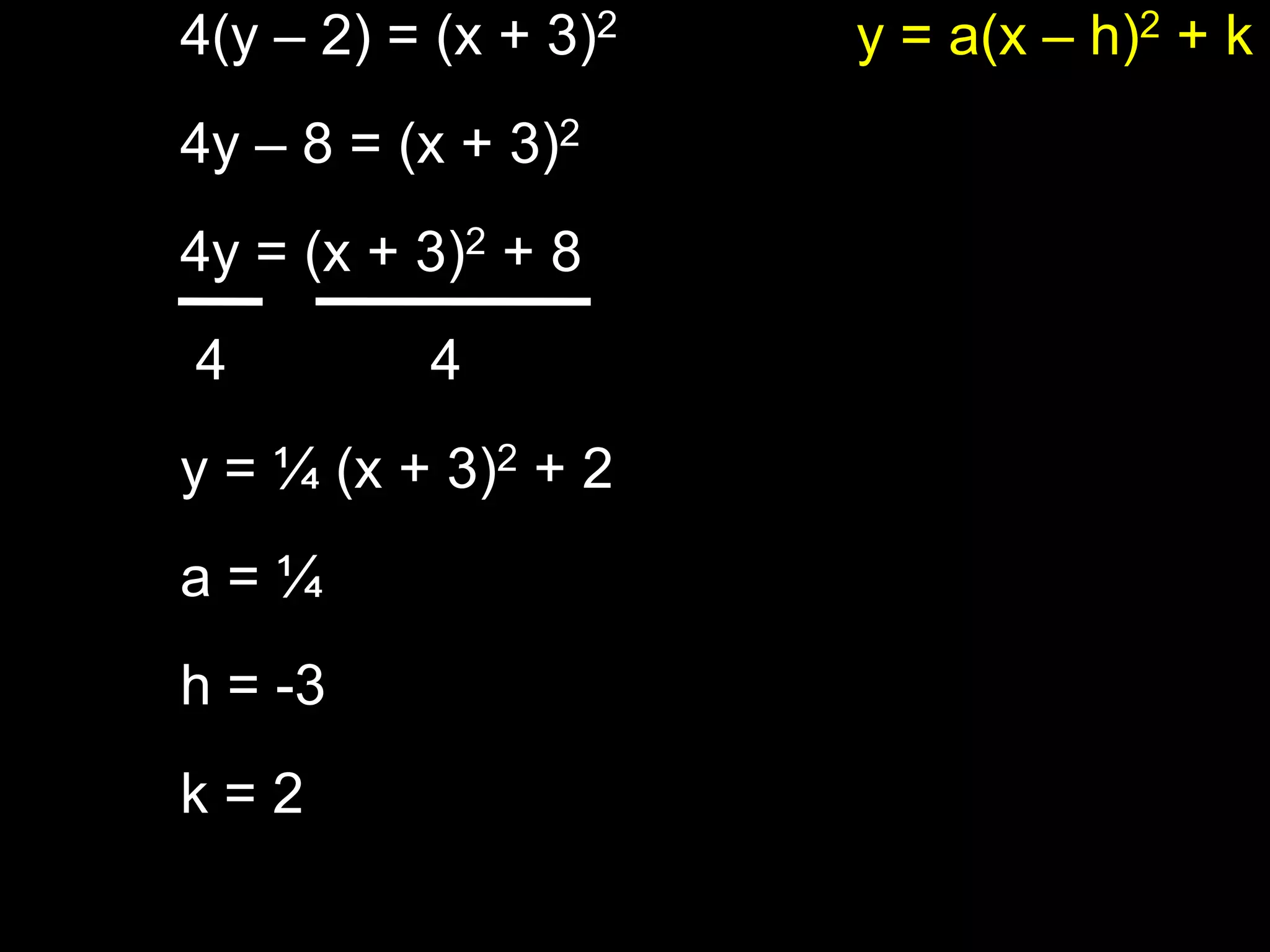
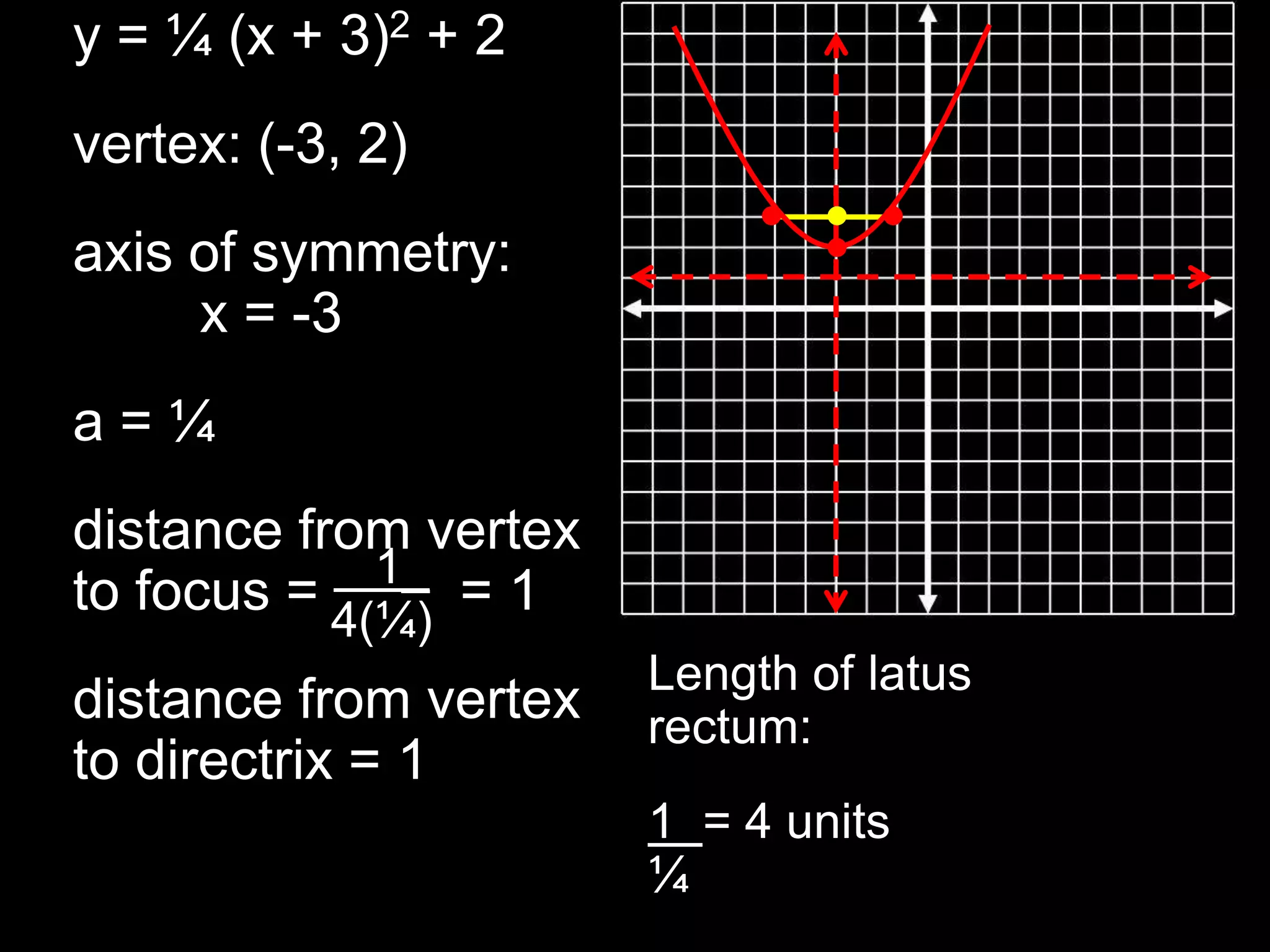
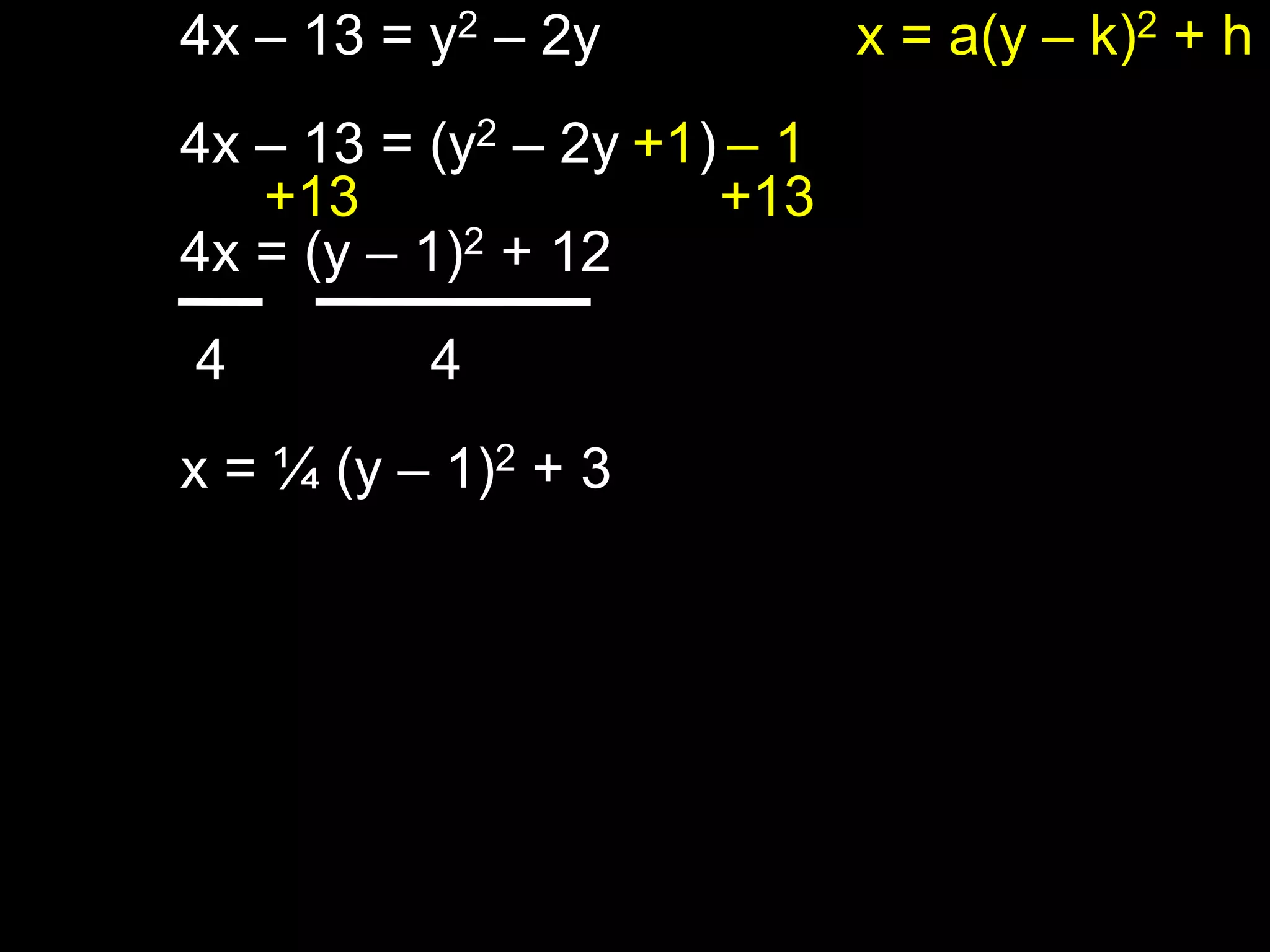
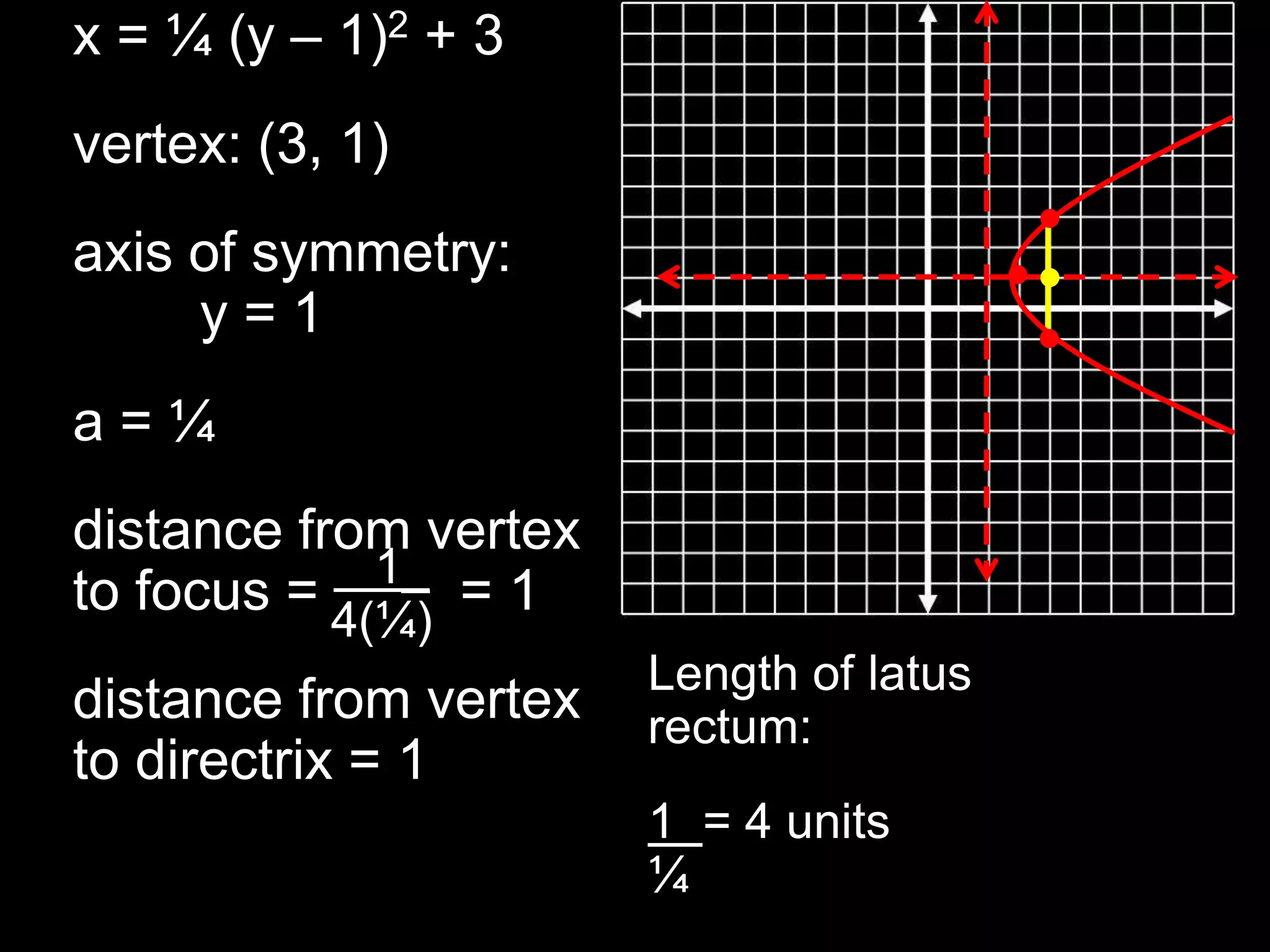
This document discusses key properties of parabolas in vertex form, including the vertex, line of symmetry, focus, directrix, and latus rectum. It provides examples of writing equations of parabolas in vertex form and extracting the vertex, axis of symmetry, and other properties. The vertex is the point (h, k) and the line of symmetry is x=h or y=k depending on the form of the equation. The focus and directrix define the parabola such that all points on the curve are equidistant from these elements.

1. Vertex form (standard form) for the equation of a parabola y = a(x – h)2 + k x = a(y – k)2 + h Vertex: (h, k) Vertex: (h, k) Line of symmetry: x = h Line of symmetry: y = k

2. Graph x = 2y2 + 8y + 9 x = (2y2 + 8y ) + 9 x = 2(y2 + 4y + 4) + 9 - 8 x = 2(y+ 2)2 + 1 Vertex: (1, -2) Axis of symmetry: y = -2 Opens to the right

3. focus latus rectum directrix All points on the parabola are equidistant from the focus and the directrix.

4. y = a(x – h)2 + k focus 1 4a same distance directrix

5. y = a(x – h)2 + k focus latus rectum 1 a length = directrix

6. Pg 422

7. 4(y – 2) = (x + 3)2 4y – 8 = (x + 3)2 4y = (x + 3)2 + 8 4 4 y = ¼ (x + 3)2 + 2 a = ¼ h = -3 k = 2 y = a(x – h)2 + k

8. y = ¼ (x + 3)2 + 2 vertex: (-3, 2) axis of symmetry: x = -3 a = ¼ distance from vertexto focus = = 1 distance from vertexto directrix = 1 1_4(¼) Length of latus rectum: 1 = 4 units¼

9. 4x – 13 = y2 – 2y 4x – 13 = (y2 – 2y ) 4x = (y – 1)2 + 12 4 4 x = ¼ (y – 1)2 + 3 x = a(y – k)2 + h +1 – 1 +13 +13

10. x = ¼ (y – 1)2 + 3 vertex: (3, 1) axis of symmetry: y = 1 a = ¼ distance from vertexto focus = = 1 distance from vertexto directrix = 1 1_4(¼) Length of latus rectum: 1 = 4 units¼