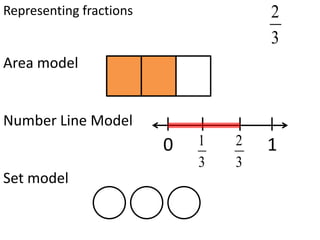
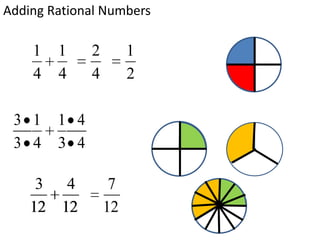
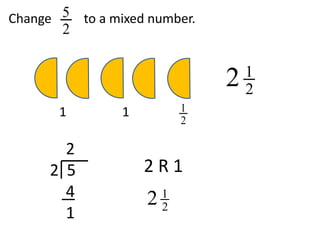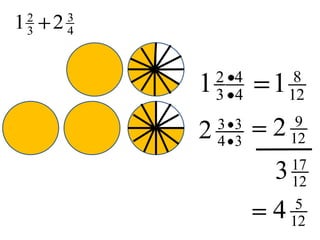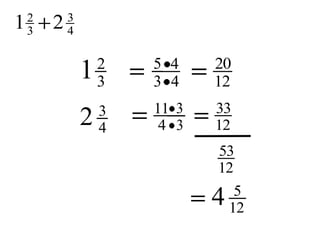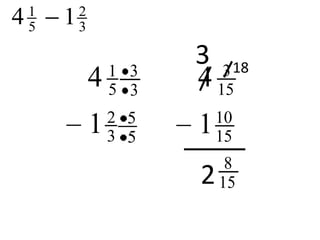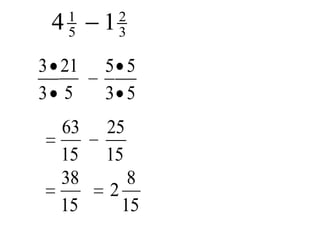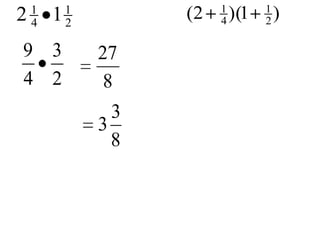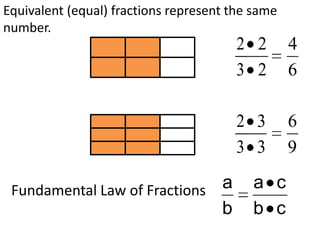
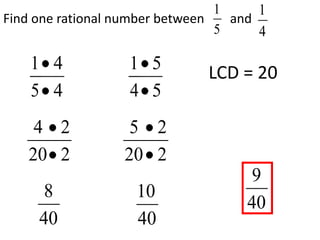
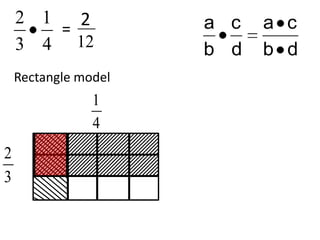
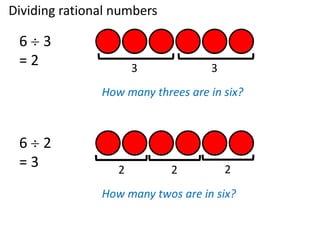
This document provides an overview of rational numbers including: - Integers and fractions written in the form a/b where a and b are integers and b ≠ 0 - Equivalent fractions represented by the same number - Ordering and comparing rational numbers - Converting between improper fractions and mixed numbers - Basic operations of addition, subtraction, multiplication, and division of rational numbers - Word problems involving rational numbers

1. Rational
Numbers

2. Integers: …, -3, -2, -1, 0, 1, 2, 3, …
A Rational Number can be written in the
form a , where a and b are integers and
b ≠ 0. b
2
3
www.visualfractions.com

3. Representing fractions 2
3
Area model
Number Line Model
0 1 2 1
3 3
Set model

4. Equivalent (equal) fractions represent the same
number.
2 2 4
3 2 6
2 3 6
3 3 9
Fundamental Law of Fractions a a c
b b c

5. 2 6
Show that and are equal by finding
3 9
a common denominator.
The least common denominator of two
fractions is the LCM of their denominators.
LCM(3,9) = 9
2 3 6
3 3 9

6. 2 6
Show that and are equal by
3 9
simplifying both fractions.
A fraction is in simplest form if its
numerator and denominator have no
common factor other than 1.
2 is simplified
6 3 2
3 9 3 3

7. 2 6
Show that and
3 9 are equal by cross
multiplying.
a c
if ad bc
b d
18 18 18 = 18
2 6 so 2 6
3 9 3 9

8. Ordering rational numbers
Place <, > or = between the two numbers:
2 3
< 0 1 2 3 4 5 6
1
7 7 7 7 7 7 7 7 7
1 3
> 7
5 5
1
1 1
< 5
5 4 1
4

9. 1 1
Find one rational number between and
5 4
1 4 1 5 LCD = 20
5 4 4 5
4 2 5 2
20 2 20 2
9
8 10
40
40 40

10. 1 1
Find two rational numbers between and
6 5
1 5 1 6 LCD = 30
6 5 5 6
5 2 6 2
30 2 30 2
10 2 12 2
60 2 60 2
21 22 23
20 24 , ,
120 120 120
120 120

11. A mixed number represents the sum of an integer
and a fraction.
1 1
1 2 1 2
1 1
1 2 1 2
-2 11
2 -1 0
1
1 1 2
2

12. 2
Change 1 3
to an improper fraction.
An improper fraction has a numerator that is greater
than or equal to its denominator.
2 3 2
1 3 3 3
2
1 3 5
3

13. Change 5 to a mixed number.
2
1
2 2
1 1 1
2
2
2 5 2R1
4 2 1
2
1

14. Adding Rational Numbers
1 1 2 1
4 4 4 2
3 1 1 4
3 4 3 4
3 4 7
12 12 12

15. 2 3
1 3 2 4
2 4 8
1 3 4 1 12
9
2 3 3
4 3
2 12
17
3 12
5
4 12

16. 2 3
1 3 2 4
2 5 4 20
1 3 3 4 12
3 11 3 33
2 4 4 3 12
53
12
5
4 12

17. Subtracting Rational Numbers
4 2 1 3 8 3 5
4 9 12 3 36 36 36
2 2 1 5 4 5 1
2 5 2 5 10 10 10

18. 1 2
4 5 1 3
1 3
3 3 18
4 5 3 4 15
2 5 10
1 3 5 1 15
8
2 15

19. 1 2
4 5 1 3
3 21 5 5
3 5 3 5
63 25
15 15
38 8
2
15 15

21. Multiplication of Rational Numbers
3·2
=6
3 groups of 2
3·½ =
3
= 1 ½ or
2
3 groups of ½

22. 2 1 2 a c a c
=
3 4 12 b d b d
Rectangle model
1
4
2
3

23. 1 1 1 1
2 4 1 2
(2 4 )(1 2 )
9 3 27
4 2 8
3
3
8

24. Dividing rational numbers
6 3
=2 3 3
How many threes are in six?
6 2
=3 2 2 2
How many twos are in six?

25. 6 ½
= 12
How many one-halfs are in six?
6 ¼
= 24
How many one-fourths are in six?

26. 1 1
3 6
=2
How many one-sixths are in one-third?
a c a d
b d b c
1 1 1 6 6
2
3 6 3 1 3

27. Jane has 20 yards of fabric. How many blouses
can she make if each blouse requires:
a) 2 yards of fabric
20 2 = 10 blouses

28. Jane has 20 yards of fabric. How many blouses
can she make if each blouse requires:
b) 2 ½ yards of fabric 8 blouses
1 5 20 2 40
20 2 2 20 2 1 5 5 =8
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20

29. Jane has 20 yards of fabric. How many blouses
can she make if each blouse requires:
c) 2 1
yards of fabric 8 blouses
3
1 7 20 3 60 4
20 2 3 20 3 1 7 7 8 7
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
d) How many yards of fabric is left over?
1 7 56 2
Fabric used: 8 2 3 8 3 3 18 3 yards
Fabric left: 20 18 2 1 1 yards
3 3