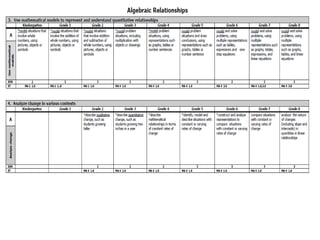
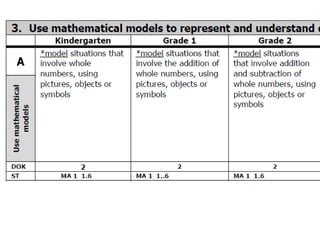
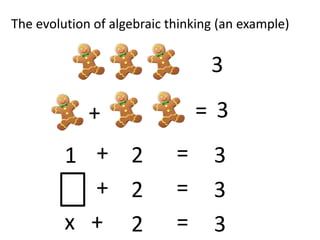
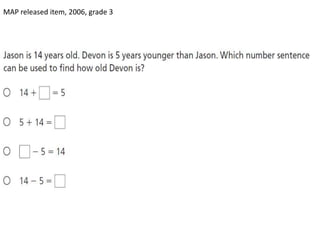
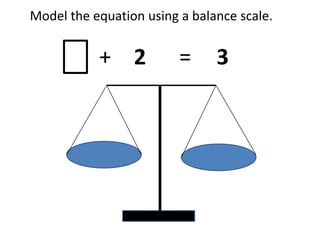
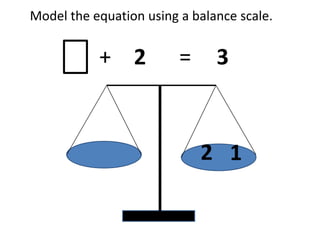
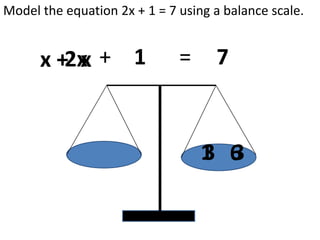
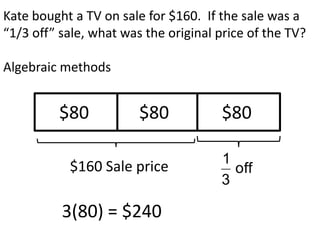
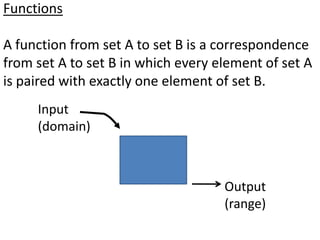
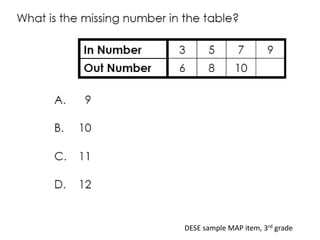
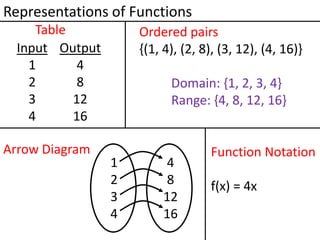
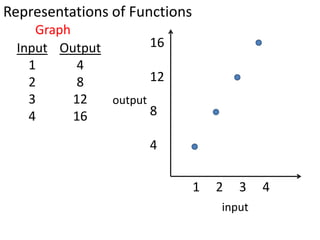
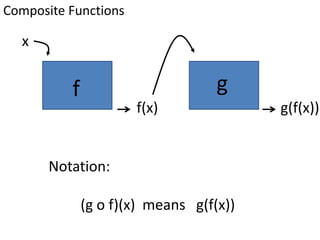
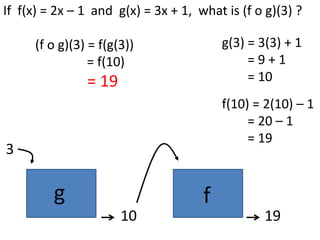
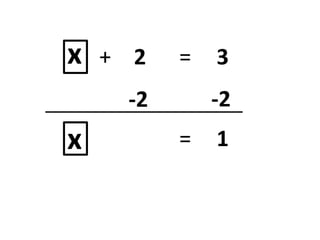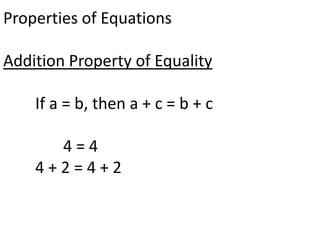Algebraic thinking involves recognizing patterns, modeling situations with symbols, and analyzing change. It relies on understanding variables to represent unknown quantities. The document traces the evolution of algebraic thinking from simple equations to more complex concepts like functions, composite functions, and properties of equations. It provides examples of how algebraic reasoning and symbols can be used to represent and solve real-world problems.

1. Algebraic
Thinking
and
Algebra

2. Algebraic Thinking involves:
•Recognizing patterns
•Modeling situations with
objects, pictures or symbols
•Analyzing the effects of change
Understanding variables (letters that
stand for an unknown) is key to algebraic
thinking.

5. The evolution of algebraic thinking (an example)
3
+ =3
1 + 2 = 3
+ 2 = 3
x + 2 = 3

6. MAP released item, 2006, grade 3

7. DESE released item 2004 MAP test, grade 4

8. MAP released item, 2006, 5th grade

9. MAP released item, 2006, grade 7

10. What does an equal sign mean?
1 + 2 = 3
1 + 2 =
ETA Cuisenaire

11. Model the equation using a balance scale.
+ 2 = 3

12. Model the equation using a balance scale.
+ 2 = 3
2 1

13. x + 2 = 3
-2 -2
x = 1

14. http://illuminations.nctm.org/ActivityDetail.aspx?ID=26
http://illuminations.nctm.org/ActivityDetail.aspx?ID=33

15. Properties of Equations
Addition Property of Equality
If a = b, then a + c = b + c
4=4
4+2=4+2

16. Multiplication Property of Equality
If a = b, then a · c = b · c
4=4
4·2=4·2

17. Distributive Property of Multiplication over
Addition
a(b + c) = a · b + a · c
2(3 + 4) = 2 · 3 + 2 · 4
5(14) = 5(10 + 4)
= 5 · 10 + 5 · 4
= 50 + 20
= 70

18. Model the equation 2x + 1 = 7 using a balance scale.
x +2x + 1
x = 7
1 6
3 3

19. If you triple a number and add 3, the result is 36. Find
the number.
Algebra Algebraic methods
3x + 3 = 36
- 3 -3
3x = 33 3 11 36 11
33 11 3
3 3
x = 11

20. Kate bought a TV on sale for $160. If the sale was a
“1/3 off” sale, what was the original price of the TV?
Algebra
Let x = the original price
original price - 1/3 of the original price = sale price
1
x - x 160
3
3 2 3
x 160
2 3 2
x = 240

21. Kate bought a TV on sale for $160. If the sale was a
“1/3 off” sale, what was the original price of the TV?
Algebraic methods
$80 $80 $80
1
$160 Sale price off
3
3(80) = $240

22. Write down any three consecutive numbers.
Multiply the first and third numbers.
Square the middle number.
What do you notice?
First times last is one less than square of middle
5 6 7
36
n–1 n n+1
35
n2
(n – 1)(n + 1)
10 11 12
121
(n – 1)(n + 1) = n2 – 1
120
difference of squares

23. Functions
A function from set A to set B is a correspondence
from set A to set B in which every element of set A
is paired with exactly one element of set B.
Input
(domain)
Output
(range)

24. DESE sample MAP item, 3rd grade

25. Representations of Functions
Table Ordered pairs
Input Output {(1, 4), (2, 8), (3, 12), (4, 16)}
1 4
2 8 Domain: {1, 2, 3, 4}
3 12 Range: {4, 8, 12, 16}
4 16
Arrow Diagram Function Notation
1 4
2 8 f(x) = 4x
3 12
4 16

26. Representations of Functions
Graph
Input Output 16
1 4
2 8 12
3 12 output
4 16 8
4
1 2 3 4
input

27. Use function notation to write a rule for the function
{(1, 2), (2, 5), (3, 8), (4, 11)}
Input Output Arithmetic sequence
1 a1 = 2 an = a1 + (n – 1)d
2 a2 = 5 a1 = 2
3 a3 = 8 d=3
4 a4 = 11
an = 2 + (n – 1)3
an = 2 + 3n – 3
an = 3n – 1
f(x) = 3x - 1

28. Composite Functions
x
f g
f(x) g(f(x))
Notation:
(g o f)(x) means g(f(x))

29. If f(x) = 2x – 1 and g(x) = 3x + 1, what is (f o g)(3) ?
(f o g)(3) = f(g(3)) g(3) = 3(3) + 1
= f(10) =9+1
= 19 = 10
f(10) = 2(10) – 1
= 20 – 1
= 19
3
g f
10 19