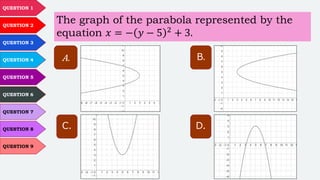
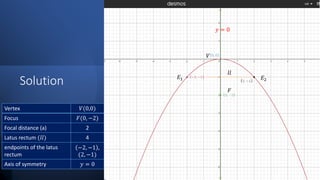
The document provides an overview of parabolas, including their definitions, properties, equations, and methods for graphing them. It contains practice questions and activities focused on identifying key features such as vertices, axes of symmetry, focus, and latus rectum. Additionally, it addresses the transformation of quadratic functions into vertex form and provides examples for better understanding.