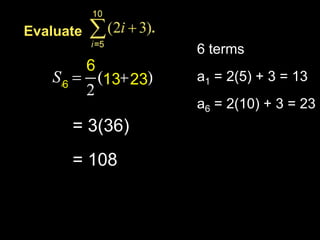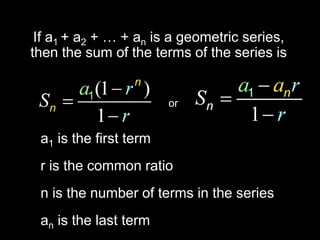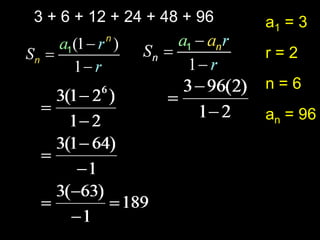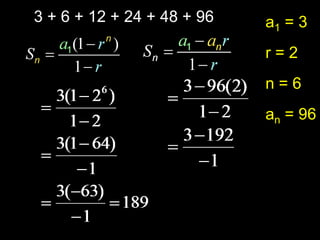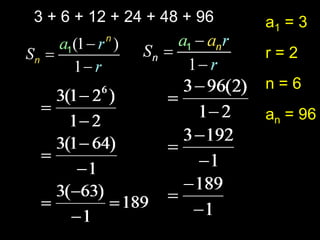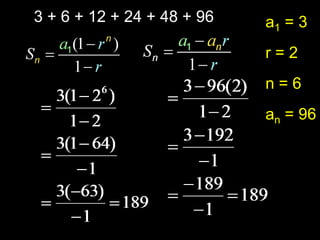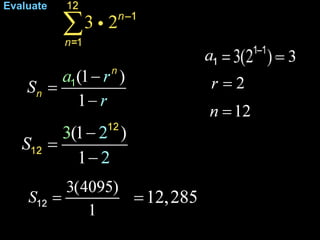The document provides information about arithmetic and geometric series. It defines arithmetic and geometric series, provides examples of finding sums of arithmetic series using formulas, and defines the key terms (first term, common ratio, number of terms, last term) used in the formula to calculate the sum of a geometric series.

1. An arithmetic series is the sum of the
indicated terms of an arithmetic sequence.
4, 6, 8 arithmetic sequence
4+6+8 arithmetic series

2. Find the sum: 6 + 13 + 20 + 27 + 34 + 41 + 48
S7 = 6 + 13 + 20 + 27 + 34 + 41 + 48
S7 = 48 + 41 + 34 + 27 + 20 + 13 + 6
2S7 = 54 + 54 + 54 + 54 + 54 + 54 + 54
2S7 = 7(54)
S7 = 7(54) = 189
2

3. Find the sum of the first 20 even numbers, beginning
with 2.

4. Find the first four terms of an arithmetic series in
which
17 20 23 26
14+__+__+__+__+29=129
+d +d +d +d +d
14
14 + 5d = 29
5d = 15
d=3

5. Sn = 4 + 8 + 12 + 16 + 20
Sigma notation can be used to express an
arithmetic series
Last value for n Formula for
generating terms
First value for n

6. How many terms are in the series
10 – 5 + 1 = 6 terms
What are the terms a1 = 2(5) + 3 = 13
in the series?
a2 = 2(6) + 3 = 15
a3 = 2(7) + 3 = 17
a4 = 2(8) + 3 = 19
a5 = 2(9) + 3 = 21
a6 = 2(10) + 3 = 23

7. Evaluate
6 terms
6
6 13 23 a1 = 2(5) + 3 = 13
6
a6 = 2(10) + 3 = 23
= 3(36)
= 108

8. Geometric Series

9. If a1 + a2 + … + an is a geometric series,
then the sum of the terms of the series is
or
a1 is the first term
r is the common ratio
n is the number of terms in the series
an is the last term

10. 3 + 6 + 12 + 24 + 48 + 96 a1 = 3
r=2
n=6
an = 96

11. 3 + 6 + 12 + 24 + 48 + 96 a1 = 3
r=2
n=6
an = 96

12. 3 + 6 + 12 + 24 + 48 + 96 a1 = 3
r=2
n=6
an = 96

13. 3 + 6 + 12 + 24 + 48 + 96 a1 = 3
r=2
n=6
an = 96

14. 3 + 6 + 12 + 24 + 48 + 96 a1 = 3
r=2
n=6
an = 96

15. 3 + 6 + 12 + 24 + 48 + 96 a1 = 3
r=2
n=6
an = 96

16. 3 + 6 + 12 + 24 + 48 + 96 a1 = 3
r=2
n=6
an = 96

17. 3 + 6 + 12 + 24 + 48 + 96 a1 = 3
r=2
n=6
an = 96

18. Evaluate

19. Find a1 in a geometric series for which
and