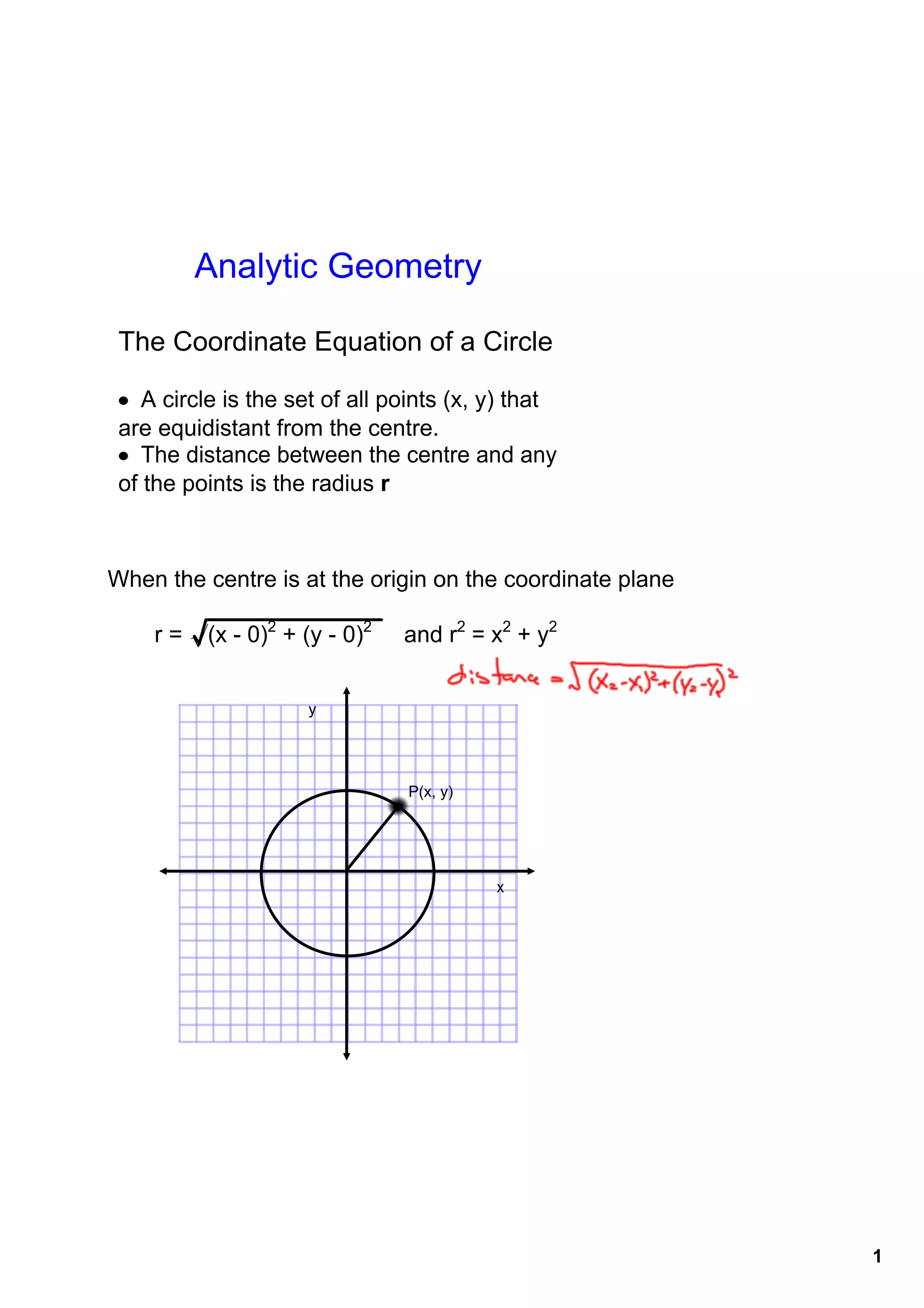
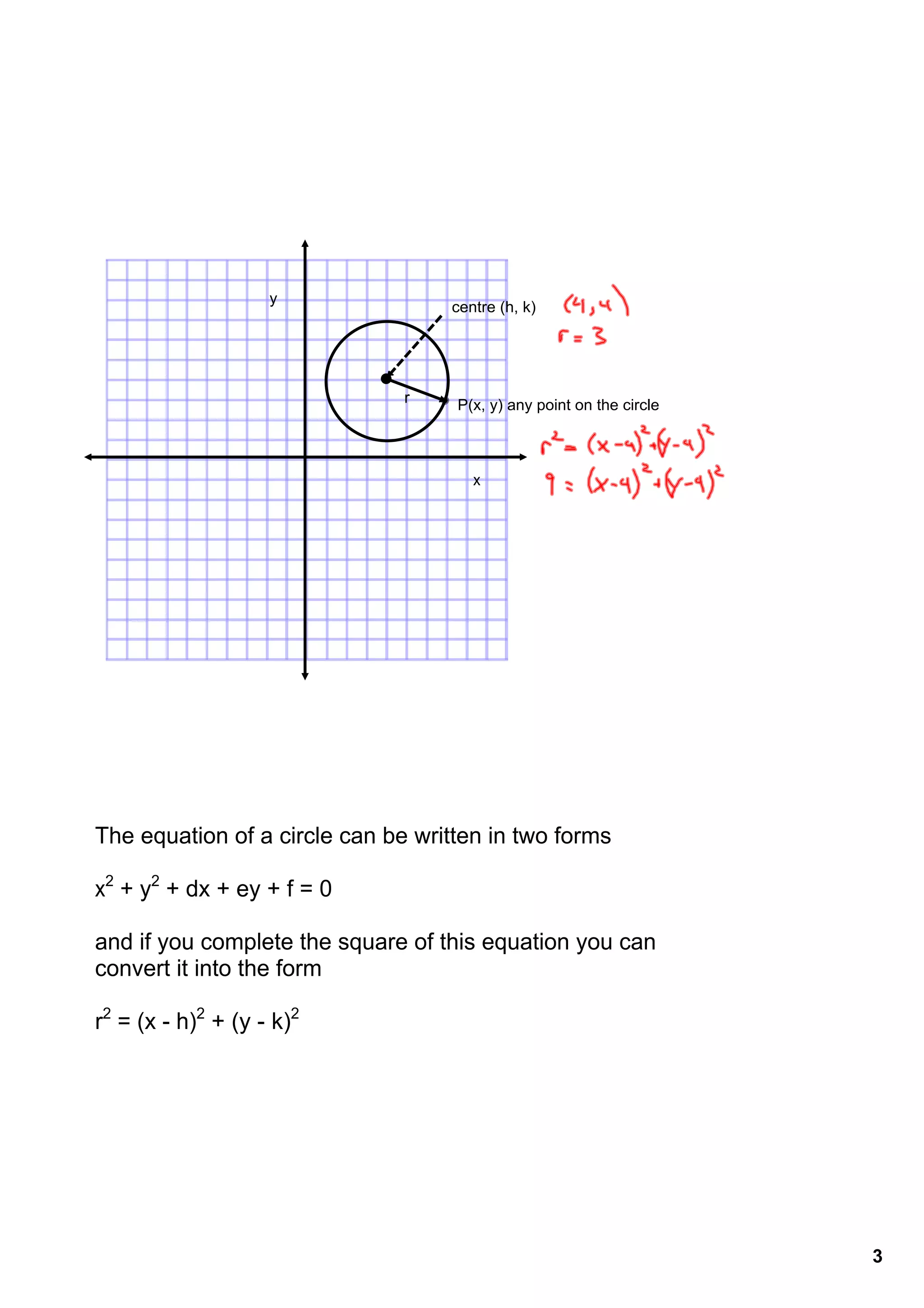
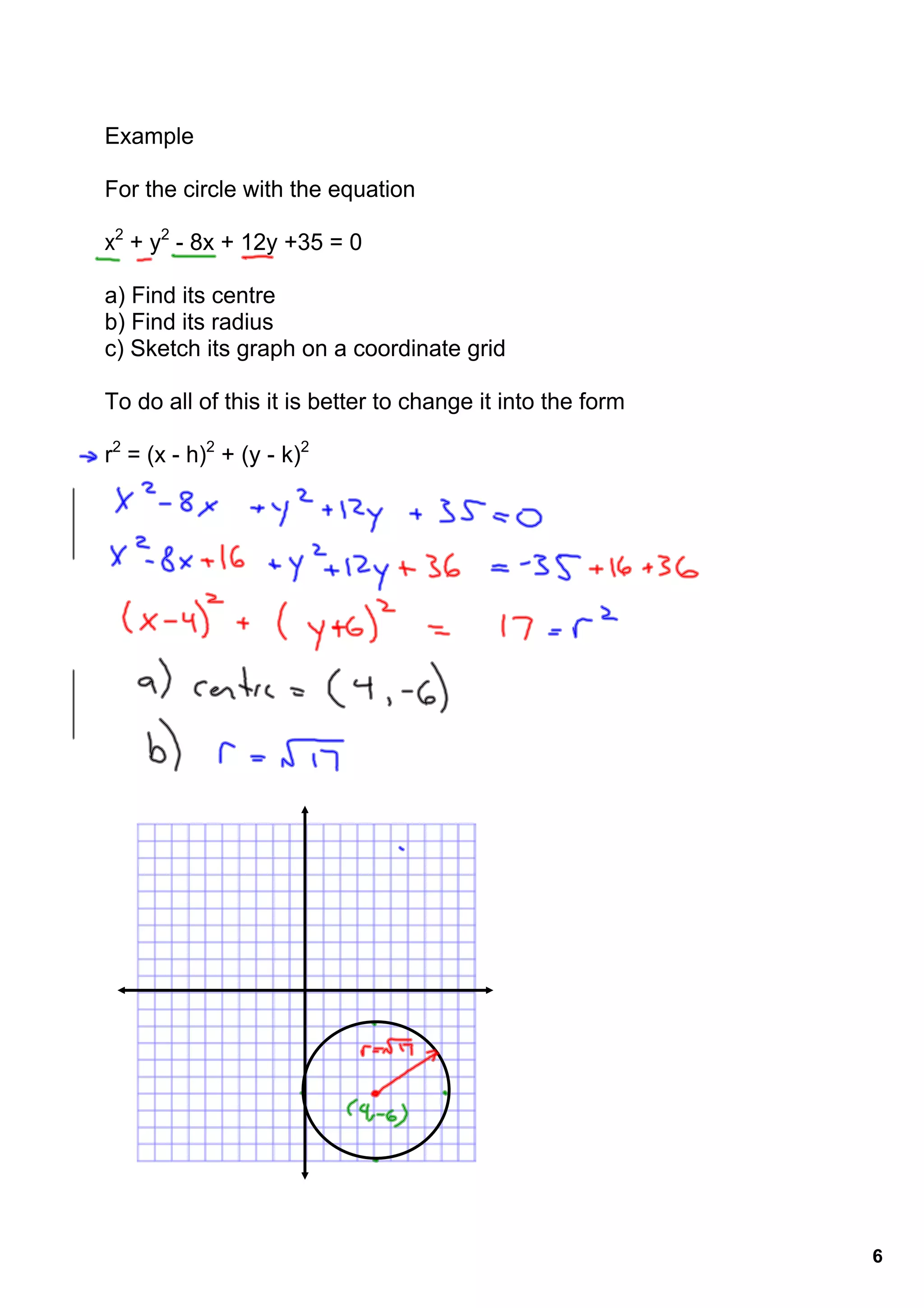
The document discusses the coordinate equation of a circle. It states that a circle can be defined as all points that are equidistant from the center point. The standard form of the equation of a circle is r2 = (x - h)2 + (y - k)2, where (h, k) are the coordinates of the center and r is the radius. It provides examples of writing the equation of a circle given properties like the center point and radius or a point on the circle.

1. Analytic Geometry
The Coordinate Equation of a Circle
• A circle is the set of all points (x, y) that
are equidistant from the centre.
• The distance between the centre and any
of the points is the radius r
When the centre is at the origin on the coordinate plane
r = √(x ­ 0)2 + (y ­ 0)2 and r2 = x2 + y2
y
P(x, y)
x
1

2. When the centre of the circle is not at the origin then:
The standard form for the equation of the radius in relation to
any point on the circle is
r = (x1 ­ x2)2 + (y1 ­ y2)2
If you know the coordinates of the centre of the circle (h,k) then
the coordinate form of the equation is
r = (x ­ h)2 + (y ­ k)2
or
r2 = (x ­ h)2 + (y ­ k)2
Note: This is the equation of the circle located with the centre
at the origin shifted h units horizontally and k units vertically
2

3. y
centre (h, k)
r P(x, y) any point on the circle
x
The equation of a circle can be written in two forms
x2 + y2 + dx + ey + f = 0
and if you complete the square of this equation you can
convert it into the form
r2 = (x ­ h)2 + (y ­ k)2
3

4. a) What is the coordinate of the
cente?
b) What is the radius?
c) Change the equation to the
form x2 + y2 + dx + ey + f = 0
4

5. Example
Give the equation of a circle whose centre is at (­2, 1)
and that has a radius of √7
Example
Give the equations in standard for that have the following
properties.
a) Centre is at (5, 0) and has a diameter of 10
b) Centre is at (4, 3) and passes through (1, 2)
c) Centre is at (0, 0) and has an area of 12π square
units
5

6. Example
For the circle with the equation
x2 + y2 ­ 8x + 12y +35 = 0
a) Find its centre
b) Find its radius
c) Sketch its graph on a coordinate grid
To do all of this it is better to change it into the form
r2 = (x ­ h)2 + (y ­ k)2
6

7. 7