Embed presentation
Downloaded 30 times























![P=[(a^-1)(Y-k)] % 26
Here this (a^-1) is not the multiplicative
inverse of a but it is the modular inverse of a.](https://image.slidesharecdn.com/dm-latest-170329171518/85/Affine-Cypher-Encryption-Decryption-24-320.jpg)

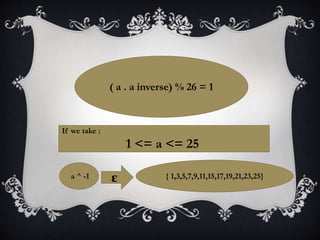
![key( a , k )=( 7,2 )
a inverse = 15
Y = 18
P = [a inverse ( Y – k) ] % 26
P = [ 15 ( 18 - 2 ) ] % 26
P = 6](https://image.slidesharecdn.com/dm-latest-170329171518/85/Affine-Cypher-Encryption-Decryption-28-320.jpg)
![key( a , k )=( 7,2 )
a inverse = 15
Y = 18
P = [a inverse ( Y – k) ] % 26
P = [ 15 ( 18 - 2 ) ] % 26
P = 6
Its CORRECT !](https://image.slidesharecdn.com/dm-latest-170329171518/85/Affine-Cypher-Encryption-Decryption-29-320.jpg)



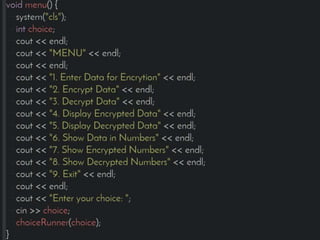
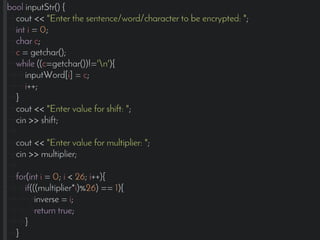
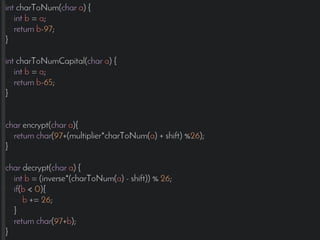
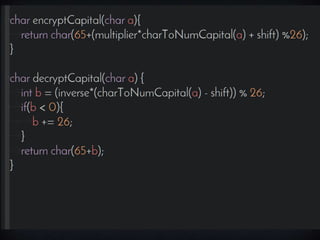

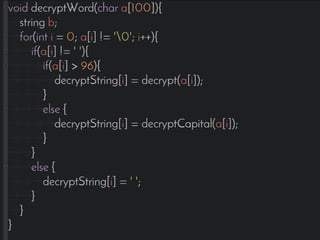

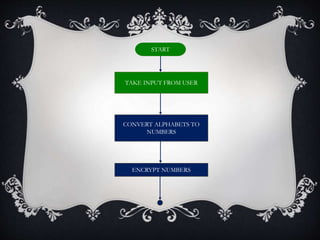
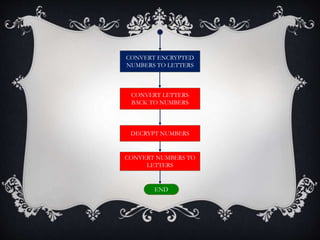


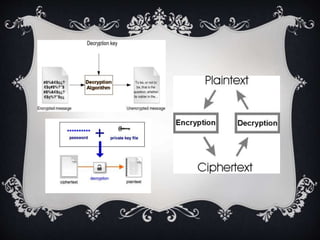
This document introduces the affine cipher encryption technique. It explains how to encrypt and decrypt messages using an affine cipher by: 1. Converting letters to numbers using their position in the alphabet. 2. Using the formula Y=(aP+k)%26 to encrypt numbers, where a is the multiplier, k is the shift, and p is the original letter's number. 3. Decrypting using the inverse of the multiplier and the same shift in the formula P=[(a^-1)(Y-k)]%26. Worked examples are provided to illustrate encrypting the letter 'g' to 's' and decrypting it back. Flowcharts outline the full encryption and decryption processes























![P=[(a^-1)(Y-k)] % 26
Here this (a^-1) is not the multiplicative
inverse of a but it is the modular inverse of a.](https://image.slidesharecdn.com/dm-latest-170329171518/85/Affine-Cypher-Encryption-Decryption-24-320.jpg)



![key( a , k )=( 7,2 )
a inverse = 15
Y = 18
P = [a inverse ( Y – k) ] % 26
P = [ 15 ( 18 - 2 ) ] % 26
P = 6](https://image.slidesharecdn.com/dm-latest-170329171518/85/Affine-Cypher-Encryption-Decryption-28-320.jpg)
![key( a , k )=( 7,2 )
a inverse = 15
Y = 18
P = [a inverse ( Y – k) ] % 26
P = [ 15 ( 18 - 2 ) ] % 26
P = 6
Its CORRECT !](https://image.slidesharecdn.com/dm-latest-170329171518/85/Affine-Cypher-Encryption-Decryption-29-320.jpg)













