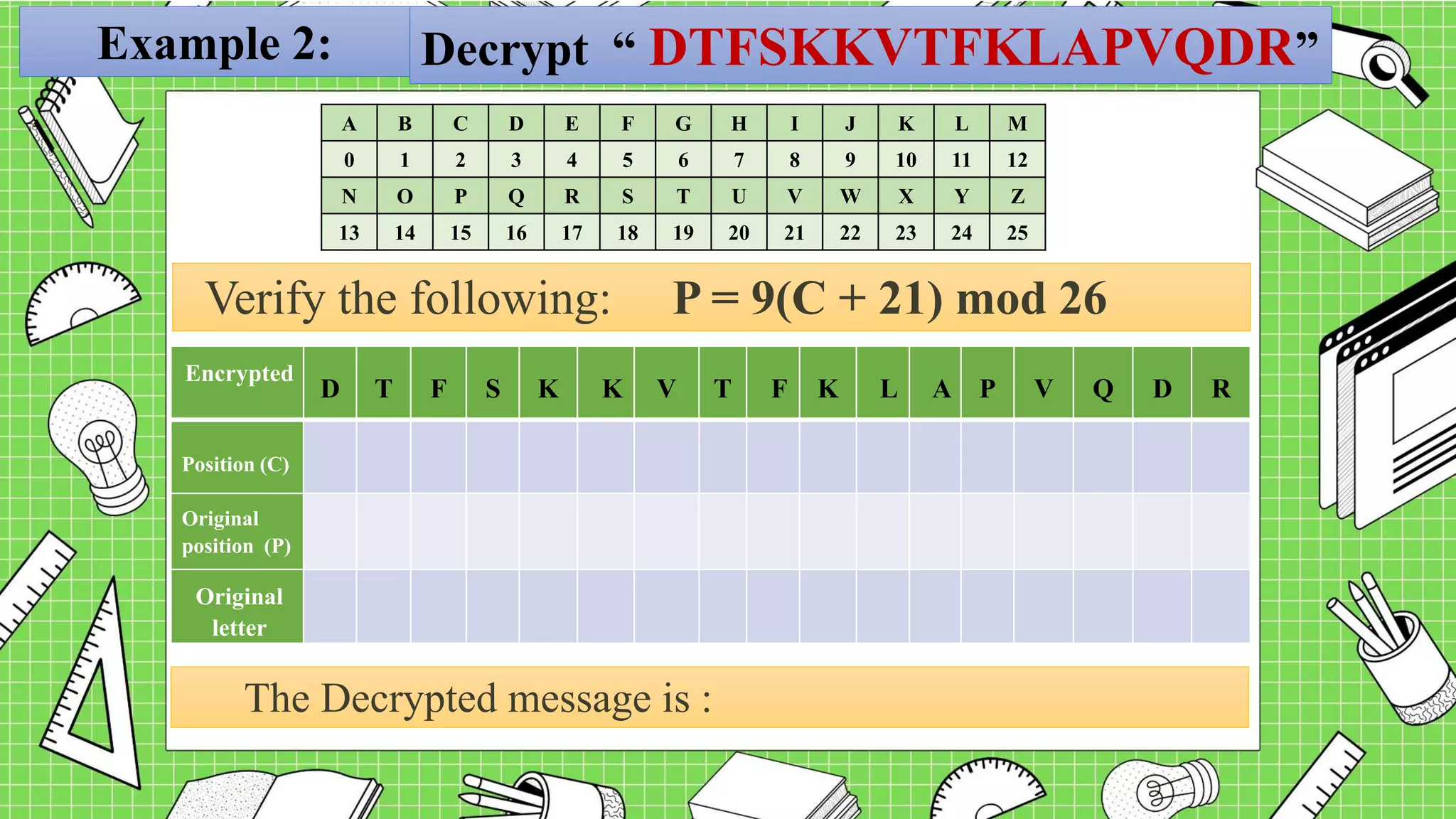
The document describes the affine cipher, which is a more complex cipher than the shift cipher. The affine cipher involves multiplying the cipher value of each letter by a value m, plus adding a constant value K, and taking the result modulo 26. It provides the encryption and decryption formulas for the affine cipher, which use m, K, and the original and ciphered positions of each letter. Examples are given to demonstrate encrypting and decrypting messages using specific m and K values with the affine cipher.

2. Affine Cipher
A more complicated
cipher formula involves
multiplying the cipher
value of each letter of the
original message. In a
way, this will be more
difficult to track than the
shift cipher technique.

3. Affine Cipher
M
Encryption Cipher (m, K): C = (mP + K) mod 26
Decryption Cipher (m, K): P = (C – K) mod 26
• 𝑃 is the original position of a letter in the given message
• 𝐶 is the shifted position (code letter),
• 𝐾 is a constant that determines the fixed number of shift
positions.

4. Affine Cipher
M
Encryption Cipher (m, K): C = (mP + K) mod 26
Decryption Cipher (m, K): P = (C – K) mod 26
As a reminder, denotes the multiplicative
inverse of m with respect to modulo 26
operation.

5. Affine Cipher
Encryption Cipher (m, K): C = (mP + K) mod 26
Decryption Cipher (m, K): P = (C – K) mod 26
Note also that the pair (m, K) is a valid
encryption cipher parameters if m and 26
are relatively prime.

6. Encryption with Affine Cipher
Encryption Formula: C = (3P + 5) mod 26
Example 1
Encrypt the message “Let us
drink coffee” using the affine
cipher pair (m, K) = (3, 5).
Encryption Cipher (m, K): C = (mP + K) mod 26
A B C D E F G H I J K L M
0 1 2 3 4 5 6 7 8 9 10 11 12
N O P Q R S T U V W X Y Z
13 14 15 16 17 18 19 20 21 22 23 24 25

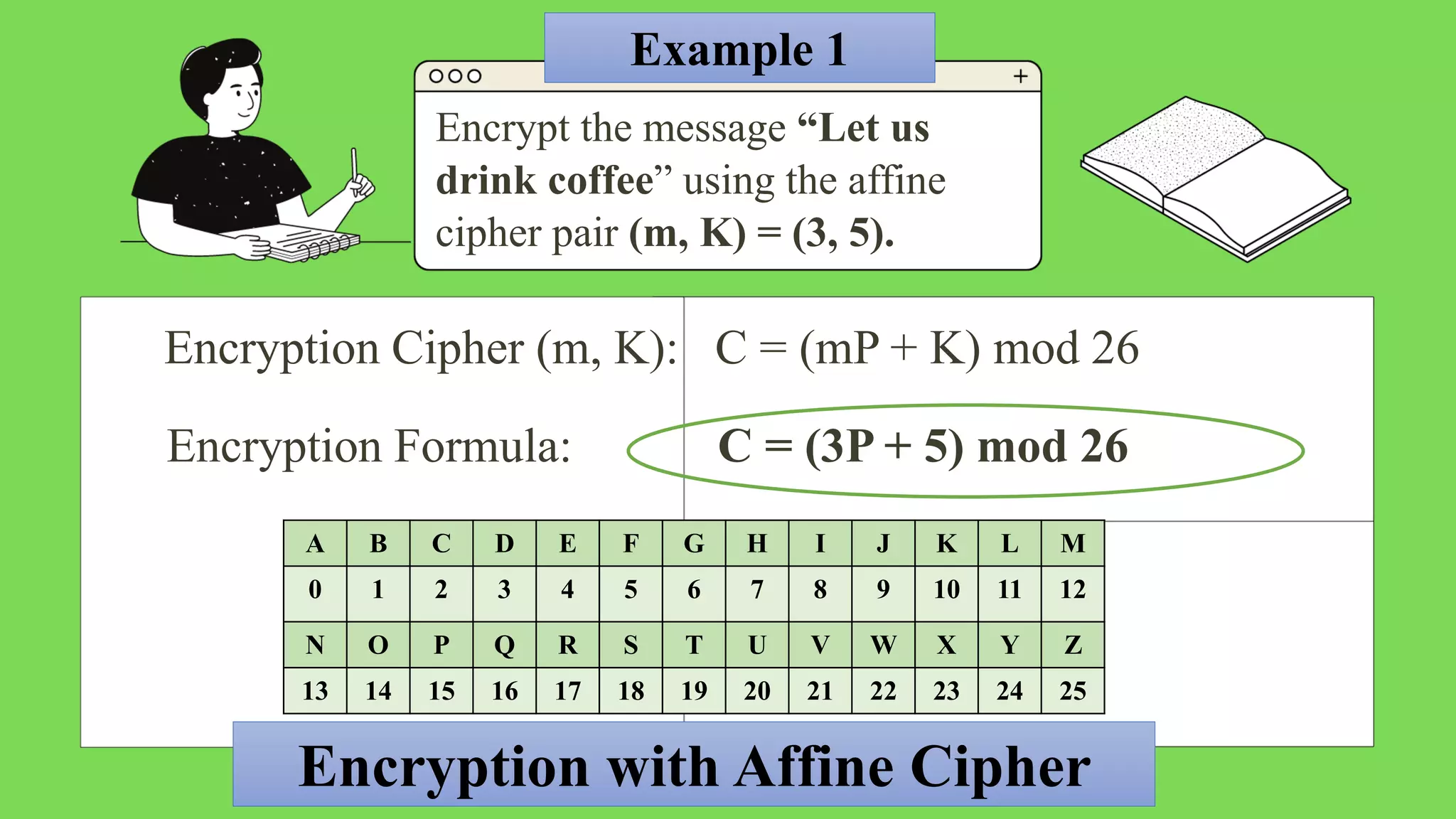
7. Example 1:
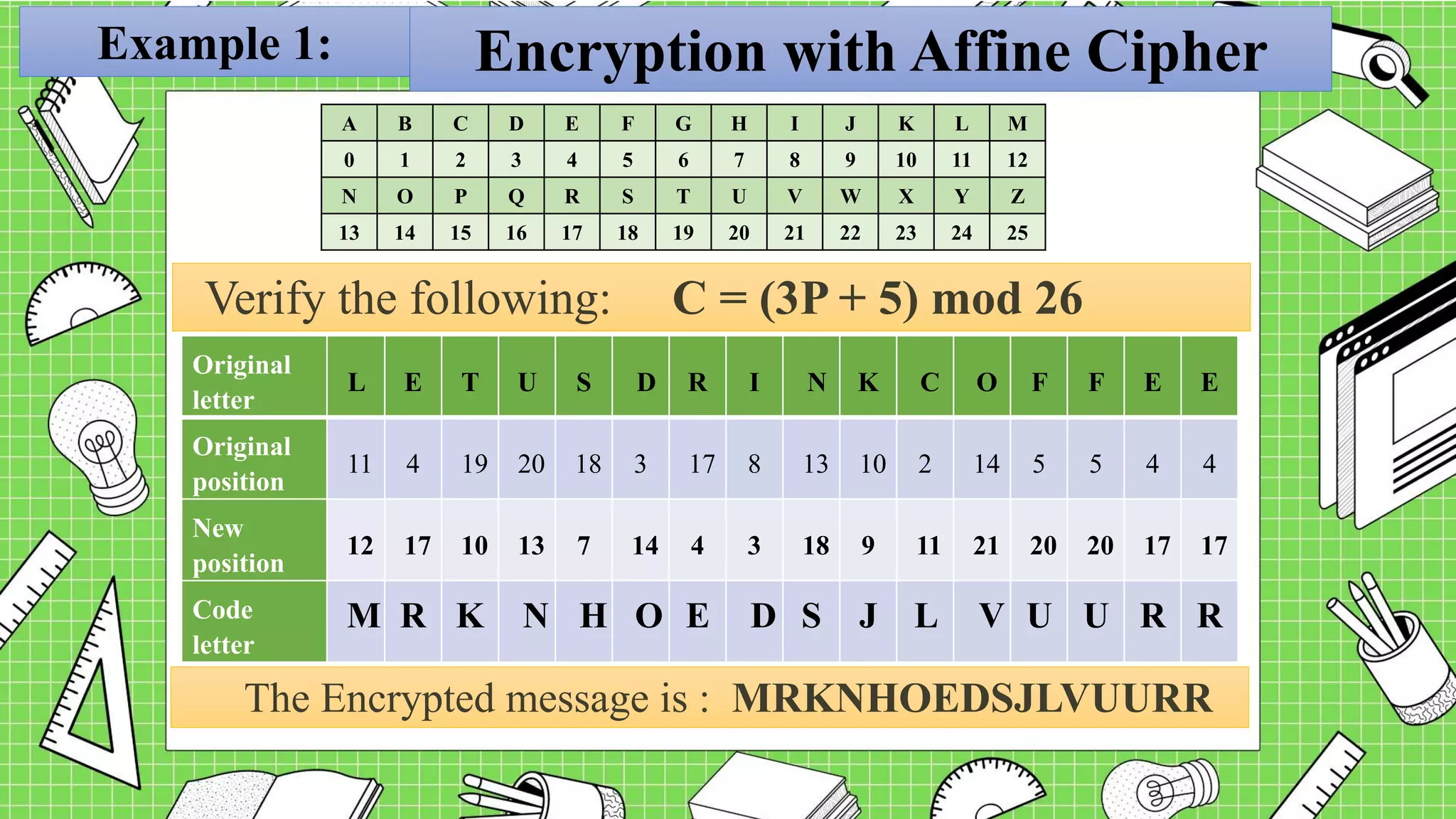
Encrypt the message “Let us drink coffee” using
the affine cipher pair (m, K) = (3, 5).
Encryption with Affine Cipher
Encryption Formula:
C = (3P + 5) mod 26
• For letter “L”, P=11
• C=[(3)(11)+5] mod 26
= 38 mod 26 = 12 the code letter for “L” is “M”
A B C D E F G H I J K L M
0 1 2 3 4 5 6 7 8 9 10 11 12
N O P Q R S T U V W X Y Z
13 14 15 16 17 18 19 20 21 22 23 24 25

8. Example 1:
Verify the following: C = (3P + 5) mod 26
Encryption with Affine Cipher
A B C D E F G H I J K L M
0 1 2 3 4 5 6 7 8 9 10 11 12
N O P Q R S T U V W X Y Z
13 14 15 16 17 18 19 20 21 22 23 24 25
Original
letter
L E T U S D R I N K C O F F E E
Original
position
11 4 19 20 18 3 17 8 13 10 2 14 5 5 4 4
New
position
12 17 10 13 7 14 4 3 18 9 11 21 20 20 17 17
Code
letter
M R K N H O E D S J L V U U R R
The Encrypted message is : MRKNHOEDSJLVUURR

9. Encryption with Affine Cipher
Encryption Formula: C = (5P + 8) mod 26
Example 2
Encrypt the message “Math is
Fun” using the affine cipher pair
(m, K) = (5, 8).
Encryption Cipher (m, K): C = (mP + K) mod 26
A B C D E F G H I J K L M
0 1 2 3 4 5 6 7 8 9 10 11 12
N O P Q R S T U V W X Y Z
13 14 15 16 17 18 19 20 21 22 23 24 25

10. Example 2:
Verify the following: C = (5P + 8) mod 26
Encryption with Affine Cipher
A B C D E F G H I J K L M
0 1 2 3 4 5 6 7 8 9 10 11 12
N O P Q R S T U V W X Y Z
13 14 15 16 17 18 19 20 21 22 23 24 25
Original letter
M A T H I S F U N
Original
position
New
position
Code letter
The Encrypted message is :

11. Affine Cipher
M
Decryption Cipher (m, K): P = (C – K) mod 26
As a reminder, denotes the multiplicative
inverse of m with respect to modulo 26
operation.

12. Example 1: Decryption with Affine Cipher
Determine a decryption formula for
the pair (m, K)=(3, 5)
Decryption Cipher (m, K): P =
𝟏
𝒎
(C – K) mod 26
1
𝑚
=
1
3
≅ 9 mod 26, since (3)(9) mod 26 = 27 mod 26 = 1
-K = -5 ≅ 21 mod 26, since 5 + 21 = 26 ≅ 0 mod 26
Again, recall that
1
3
denotes the multiplicative inverse of 3 mod 26
while -5 denotes the additive inverse of 5 mod 26.

13. Example 1: Decrypt for (m, K)=(3, 5)
mod 26, since (3)(9) mod 26 = 27 mod 26 = 1
-K = -5 ≅ 21 mod 26, since 5 + 21 = 26 ≅ 0 mod 26
Again, recall that
1
3
denotes the multiplicative inverse of 3 mod 26
while -5 denotes the additive inverse of 5 mod 26.
1
𝑚
=
1
3
≅ 9
Decryption Cipher (m, K): P =
𝟏
𝒎
(C – K) mod 26
Decryption formula:
P = 9(C + 21) mod 26 or
P = 9(C – 5) mod 26

14. Example 1: Decrypt : MRKNHOEDSJLVUURR
Decryption formula:
P = 9(C + 21) mod 26 or
P = 9(C – 5) mod 26
Let us use : P = 9(C + 21) mod 26

15. Example 1: Decrypt : MRKNHOEDSJLVUURR
Decryption formula:
P = 9(C + 21) mod 26
For letter “M”, C=12
==> P=9(12+21) mod 26
= 9 (33) mod 26
= 297 mod 26 = 11
==> P = 11, corresponds to letter “L”
A B C D E F G H I J K L M
0 1 2 3 4 5 6 7 8 9 10 11 12
N O P Q R S T U V W X Y Z
13 14 15 16 17 18 19 20 21 22 23 24 25

16. Example 1:
Let us use : P = 9 (C + 21) mod 26
A B C D E F G H I J K L M
0 1 2 3 4 5 6 7 8 9 10 11 12
N O P Q R S T U V W X Y Z
13 14 15 16 17 18 19 20 21 22 23 24 25
Encrypted
M R K N H O E D S J L V U U R R
Position (C) 12 17 10 13 7 14 4 3 18 9 11 21 20 20 17 17
Original
position (P)
Original
letter
The Decrypted message is :
11 4 19 20 18 3 17 8 13 10 2 14 5 5 4 4
L E T U S D R I N K C O F F E E
LET US DRINK COFFEE
Decrypt : MRKNHOEDSJLVUURR

17. Example 1: Decrypt : MRKNHOEDSJLVUURR
Decryption formula:
P = 9(C + 21) mod 26 or
P = 9(C – 5 ) mod 26
Let us use : P = 9(C - 5) mod 26

18. Example 1: Decrypt : MRKNHOEDSJLVUURR
Decryption formula:
P = 9(C - 5) mod 26
For letter “M”, C=12
==> P=9(12-5) mod 26
= 9 (7) mod 26
= 63 mod 26 = 11
==> P = 11, corresponds to letter “L”
A B C D E F G H I J K L M
0 1 2 3 4 5 6 7 8 9 10 11 12
N O P Q R S T U V W X Y Z
13 14 15 16 17 18 19 20 21 22 23 24 25

19. Example 1:
Let us use : P = 9 (C – 5 ) mod 26
A B C D E F G H I J K L M
0 1 2 3 4 5 6 7 8 9 10 11 12
N O P Q R S T U V W X Y Z
13 14 15 16 17 18 19 20 21 22 23 24 25
Encrypted
M R K N H O E D S J L V U U R R
Position (C) 12 17 10 13 7 14 4 3 18 9 11 21 20 20 17 17
Original
position (P)
Original
letter
The Decrypted message is :
11 4 19 20 18 3 17 8 13 10 2 14 5 5 4 4
L E T U S D R I N K C O F F E E
LET US DRINK COFFEE
Decrypt : MRKNHOEDSJLVUURR

20. Example 2: Decrypt “ DTFSKKVTFKLAPVQDR”
Decrypt “DTFSKKVTFKLAPVQDR”
using the affine cipher pair (m, K) = (3, 5).
Decryption formula:
P = 9(C + 21) mod 26 or
P = 9(C – 5 ) mod 26

21. Example 2:
Verify the following: P = 9(C + 21) mod 26
A B C D E F G H I J K L M
0 1 2 3 4 5 6 7 8 9 10 11 12
N O P Q R S T U V W X Y Z
13 14 15 16 17 18 19 20 21 22 23 24 25
Encrypted
D T F S K K V T F K L A P V Q D R
Position (C)
Original
position (P)
Original
letter
The Decrypted message is :
Decrypt “ DTFSKKVTFKLAPVQDR”

22. 1. Apply Affine Cipher using (m, K) = (3, 4) to
encrypt the message: “STOPTONIGHT”
2. Apply Affine Cipher using (m, K) = (3, 7) to
decrypt the message: “HWWFUTNFABTG”

23. FOR LISTENING