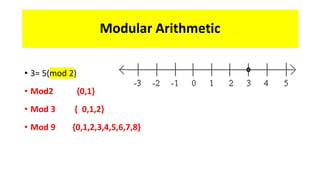
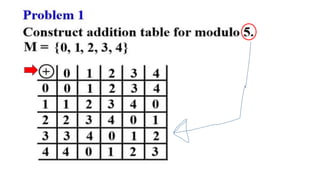
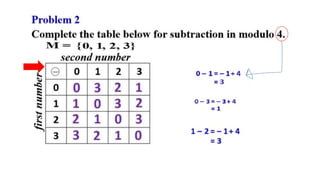
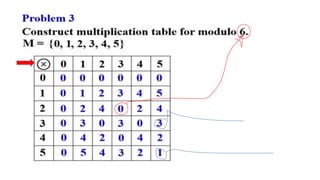
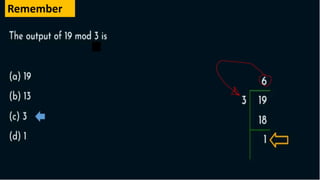
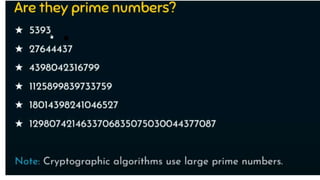
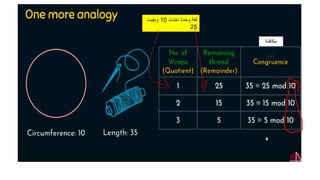
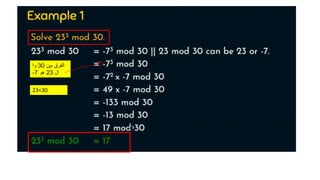
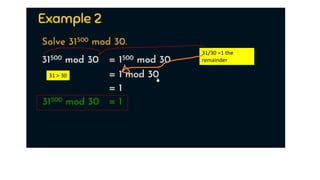
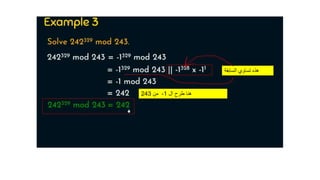
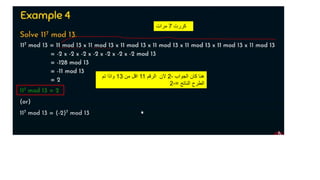
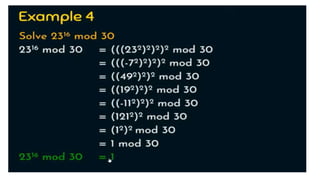
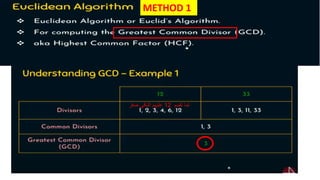
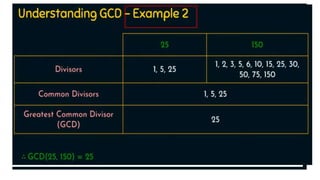
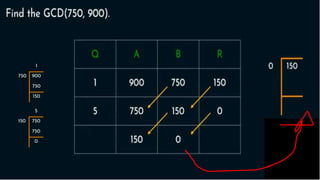
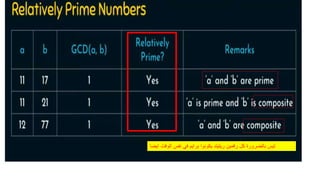
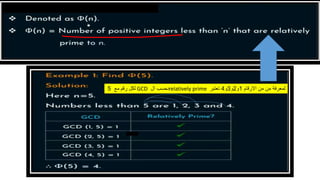
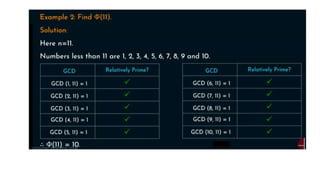
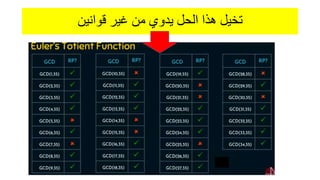
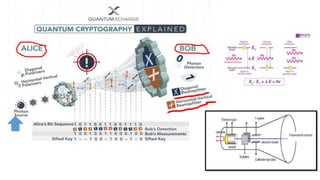
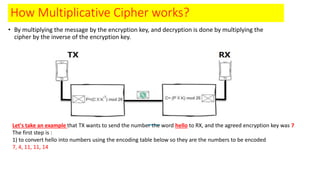
Modern cryptography relies heavily on abstract algebra and number theory. Modular arithmetic involves dividing numbers and taking the remainder. The multiplicative cipher encrypts messages by multiplying them by an encryption key, and decrypts them by multiplying the cipher by the inverse of the key. The affine cipher combines the additive and multiplicative ciphers, applying one then the other, to further strengthen security.

1. Chapter 4
Algebra and Number theory
in Cryptography

3. • The Modern cryptography is heavily dependent on:
abstract algebra and number theory.

5. Modular Arithmetic
• 3= 5(mod 2)
• Mod2 {0,1}
• Mod 3 { 0,1,2}
• Mod 9 {0,1,2,3,4,5,6,7,8}

9. Remember

10. 10X10

13. ‫تعود‬ ‫اليومية‬ ‫الساعة‬
‫رقم‬ ‫الى‬ ‫تصل‬ ‫عندما‬
‫ال‬ ‫حال‬ ‫وهذا‬ ‫معين‬
Modulus
1----12

14. ‫اخذت‬ ‫وحدة‬ ‫لفة‬
10
‫وبقيت‬
25
‫مكافئة‬

16. ‫هنا‬
10
‫تقسيم‬
6
=
1
‫والباقي‬
4
‫مش‬
2
‫على‬ ‫قسمنا‬ ‫انا‬ ‫فرضنا‬ ‫لو‬
12
‫واالجابة‬
2
‫و‬
2
‫في‬
12
‫تساوي‬
24
‫من‬
38
=
14

22. ‫بين‬ ‫الفرق‬
30
‫وا‬
‫ال‬
23
‫هو‬
7
-
23<30

23. 31/30 =1 the
remainder
31 > 30

24. ‫السابقة‬ ‫تساوي‬ ‫هذه‬
‫ال‬ ‫طرح‬ ‫هنا‬
1
-
‫من‬
243

25. ‫كررت‬
7
‫مرات‬
‫الجواب‬ ‫كان‬ ‫هنا‬
-
2
‫الرقم‬ ‫الن‬
11
‫من‬ ‫اقل‬
13
‫تم‬ ‫واذا‬
‫الناتج‬ ‫الطرح‬
=
-
2

28. ‫تقسم‬ ‫لما‬
12
‫صفر‬ ‫الباقي‬ ‫عليهم‬
METHOD 1

30. ‫الرقم‬ ‫يوضع‬ ‫هنا‬
‫االكبر‬
33 ‫االصغر‬ ‫الرقم‬
12
‫كوشن‬
‫صفر‬ ‫ليست‬ ‫طالما‬
‫الحل‬ ‫نكرر‬ ‫نبقى‬
3 is the biggest number can be divided by 12 and 33

32. HW

33. GCD Method 2

34. STOP

35. 83 and 19 are relatively prime

36. Relatively Prime (Co-Prime) Numbers

39. ‫النها‬
3
‫مش‬
1

40. ‫ايضا‬ ‫الوقت‬ ‫نفس‬ ‫في‬ ‫برايم‬ ‫يكونوا‬ ‫ريليتد‬ ‫رقمين‬ ‫كل‬ ‫بالضرورة‬ ‫ليس‬

42. ‫االرقام‬ ‫من‬ ‫من‬ ‫لمعرفة‬
1
‫و‬
2
‫و‬
3
‫و‬
4
‫تعتبر‬
relatively prime
‫ال‬ ‫نحسب‬
GCD
‫رقم‬ ‫لكل‬
‫مع‬
5

44. ‫ليست‬
1

45. Solved examples

46. ‫للحفظ‬ ‫قوانين‬

47. ‫بالقو‬ ‫السابق‬ ‫المثال‬ ‫حل‬
‫انين‬

49. ‫هناك‬ ‫ان‬ ‫اي‬
24
‫من‬ ‫اقل‬ ‫رقم‬
35
‫وتحوي‬
relative prime numbers
‫يعتبر‬ ‫ال‬ ‫رقم‬ ‫على‬ ‫المثال‬ ‫هذا‬prime number
‫للحب‬ ‫وقت‬ ‫سيستغرق‬ ‫كان‬ ‫كم‬ ‫قانةن‬ ‫من‬ ‫تتخيل‬ ‫ان‬ ‫لك‬

50. ‫قوانين‬ ‫غير‬ ‫من‬ ‫يدوي‬ ‫الحل‬ ‫هذا‬ ‫تخيل‬

54. • Quantum cryptography is different from traditional cryptographic
systems in that it relies on physics, rather than mathematics, as the
key aspect of its security model.

57. Multiplicative Cipher
Encryption in the Multiplicative Cipher algorithm is done by :
- multiplying the message by the encryption key,
- and decryption is done by multiplying the cipher by the inverse of the
encryption key.
Multiplicative group: The group whose elements have the greatest common divisor and the group number is 1,
and all of whose elements are less than the group number.
Group number means the number below the letter Z, such as multiplication groups.

58. • The inverse of a number (Inverse): which is symbolized by the number raised to the
power of negative one, the inverse of the number.
• The inverse of p is the smallest number that makes the remainder of (p * a) ÷ b equal
to 1.
• Attention: the combination of the multiple of 5 and the remainder of the division of 5
are the same.
• Important: for an inverse to exist, the greatest common divisor of the number and the
divisor for the remainder must be 1.
• As following examples:
The inverse of p is the smallest number that makes the remainder of the division of (p * a) ÷ p 1.
Try to understand the writing here do not make algebraic and mathematical.
(1) Inverse of 3 remainder of division by 5.
a = 3, b = 5. The inverse of p is the smallest number that makes (p * a)% b = 1.
If inverse of 3 = 2.
(2) Inverse of 4 remainder of division by 5.
a = 4, b = 5.
Find p where (p * 4)% 5 = 1.
You find the number = 4, where 16% 5 = 1.
And so on ..
Note that the inverse is just the smallest number that satisfies the equation

59. How Multiplicative Cipher works?
• By multiplying the message by the encryption key, and decryption is done by multiplying the
cipher by the inverse of the encryption key.
Let's take an example that TX wants to send the number the word hello to RX, and the agreed encryption key was 7
The first step is :
1) to convert hello into numbers using the encoding table below so they are the numbers to be encoded
7, 4, 11, 11, 14

60. Encrypt numbers using an encryption algorithm
(7 * 7) % 26 = 23
(4*7) % 26 = 2
(11 * 7) % 26 = 25
(11 * 7) % 26 = 25
(14 * 7) % 26 = 20
Convert numbers to letters using the cipher table
23 = x
2 = c
25 = z
20 = u
The encrypted message becomes xczzu

61. • Example of decryption using the multiplex encryption algorithm
• We find the inverse of the encryption key, 7, which is 15. Why?
• Because 15 is the smallest number, the remainder of 7*15/26 equals 1.
• We convert the characters of the xczzu code into numbers
• 23 = x
• 2 = c
• 25 = z
• 20 = u
• We perform the decoding algorithm
• (23 * 15) % 26 = 7
• (2 * 15) % 26 = 4
• (25 * 15) % 26 = 11
• (20 * 15) % 26 = 14
• Convert the numbers into letters 7, 4, 11, 11, 14 and the word is hello.

62. Affine Cipher
• combining more than one encryption algorithm might result in a
more secure code: Avini coding algorithm applies this important
concept.
• applying the algorithm more than once always increases the strength
of the cipher, and that applying more than one encryption algorithm
on the message will increase the strength of the cipher. The code
always.

63. • Avini encryption algorithm have two ways,
• 1) direct encryption
• 2) detailed encryption:
• Detailed encryption is that you use your knowledge that the affine
algorithm consists of the addition encryption algorithm and the
Multiplicative encryption algorithm, and you apply the Multiplacteive
encryption first and then the addition encryption, and thus you have
produced a code by the affine algorithm. However, when decoding, you
must take into account that it reverses the order of application of the
two algorithms, that is, you apply the addition decoding algorithm first,
and then the multiplication algorithm decoding.
• Direct encryption is to use a single algorithm that combines both the
addition encryption algorithm and the multiplex encryption algorithm,
as shown below.
• Avene coding algorithm

64. • The number of keys in the affine encryption algorithm
• You will not miss that there are two encryption keys K1 and k2,
because the algorithm uses two algorithms, the first key is used in the
Multiplactive
• encryption algorithm and the second is used in the addition
encryption algorithm. And the existence of the key does not mean
that they are related to each other in any way. The first key may be
any number, and the second key may also be any number.
• But if you wondered about what is the inverse of the encryption key
K^-1, it is the inverse of the encryption key, which explained the
encryption method by Multiplicative.

65. •An example of encoding with the Avini algorithm
• You and I will encrypt oolom using encryption keys 3 and 5.
• We convert the word oolom into numbers using the coding table (if you don't know it, you will find it
here) to be
• 14, 14, 11, 14, 12.
• We encode these values ​​using direct encoding and converting the encoding value through the coding table
• cipher 14 = 21 = v.
• cipher 11 = 12 = m.
• cipher 12 = 15 = p.
• The code becomes vvmvp.

66. An example of decoding with the Avini algorithm
• Well, you got the code that your friend sent you in the name of the blog where he found this
algorithm, and the code was vvmp, and you know that the key is 3 and 5.
• The first step is to get the inverse of the first key (3), (how to get the inverse is explained here)
• Inverse of 3 = 9.
• Convert letters to numbers using the encoding and decoding table
• v = 21, decoding = ( (21 - 5) * 9) % 26 = 14 = o.
• m = 12, decoder = 11 = o.
• p = 15, decoder = 12 = p.
• The original message becomes oolum.

67. • https://www.oolom.com/1897/%D8%AE%D9%88%D8%A7%D8%B1%
D8%B2%D9%85%D9%8A%D8%A9-
%D8%A7%D9%84%D8%AA%D8%B4%D9%81%D9%8A%D8%B1-
%D8%A8%D8%A7%D9%84%D9%85%D8%B6%D8%A7%D8%B9%D9%8
1%D8%A9-multiplicative-cipher/
• ‫للتشفير‬ ‫رائع‬ ‫مثال‬