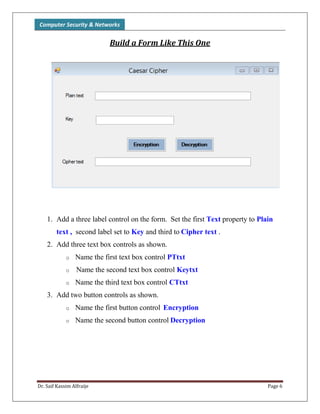
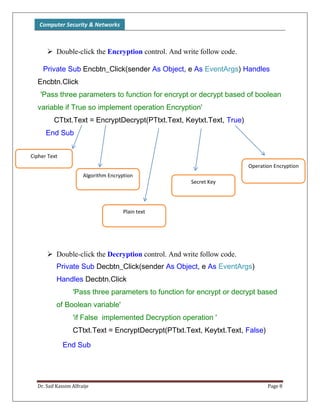
The document discusses classical encryption techniques, focusing on monoalphabetic ciphers and the Caesar cipher. It provides details on how the Caesar cipher works, including encrypting and decrypting messages by shifting letters of the alphabet based on a key. Code examples are given for implementing the Caesar cipher in a program using a dictionary to store the alphabet and encrypting/decrypting strings by adding or subtracting the key from letter numbers modulo 26.