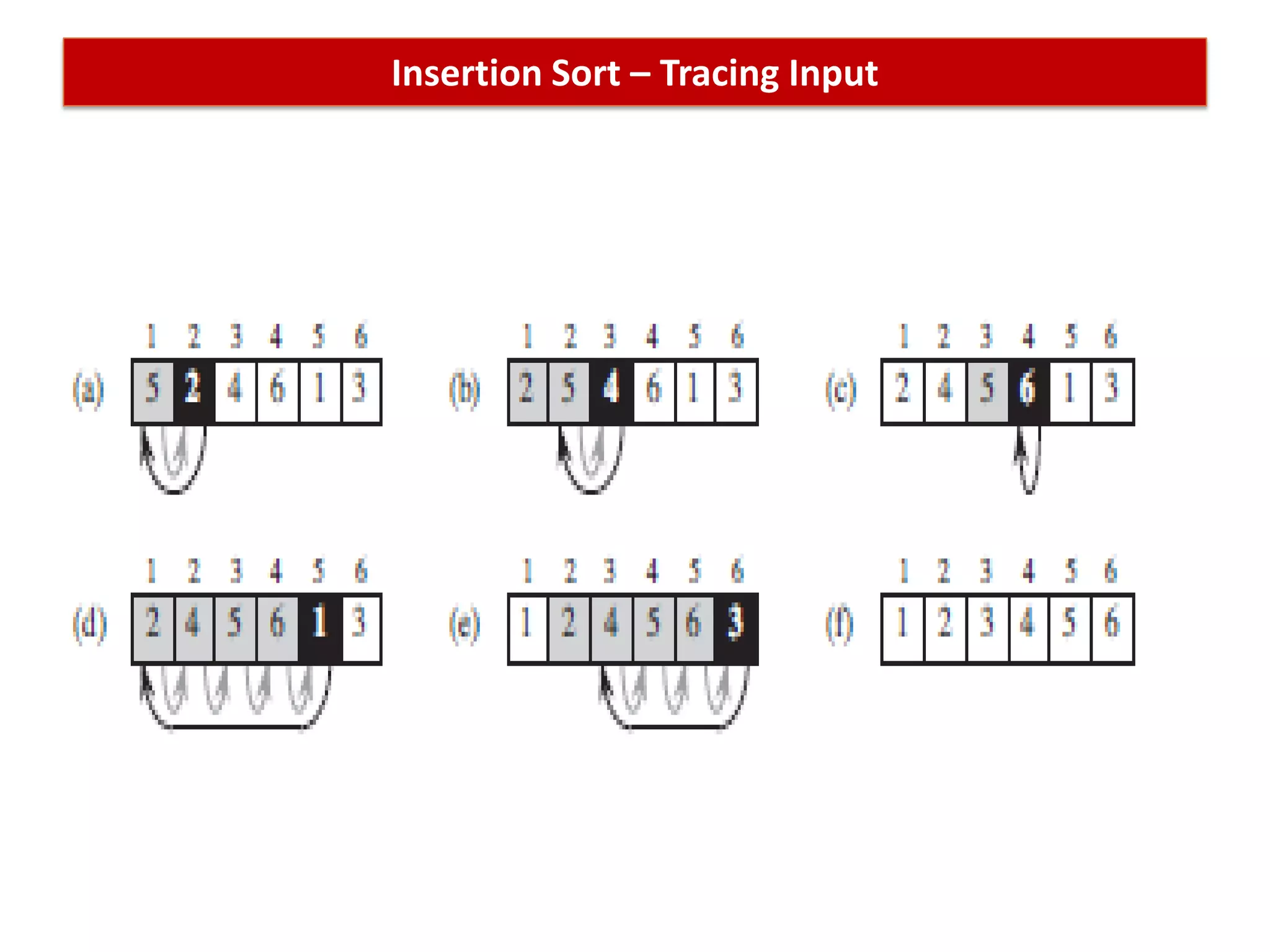
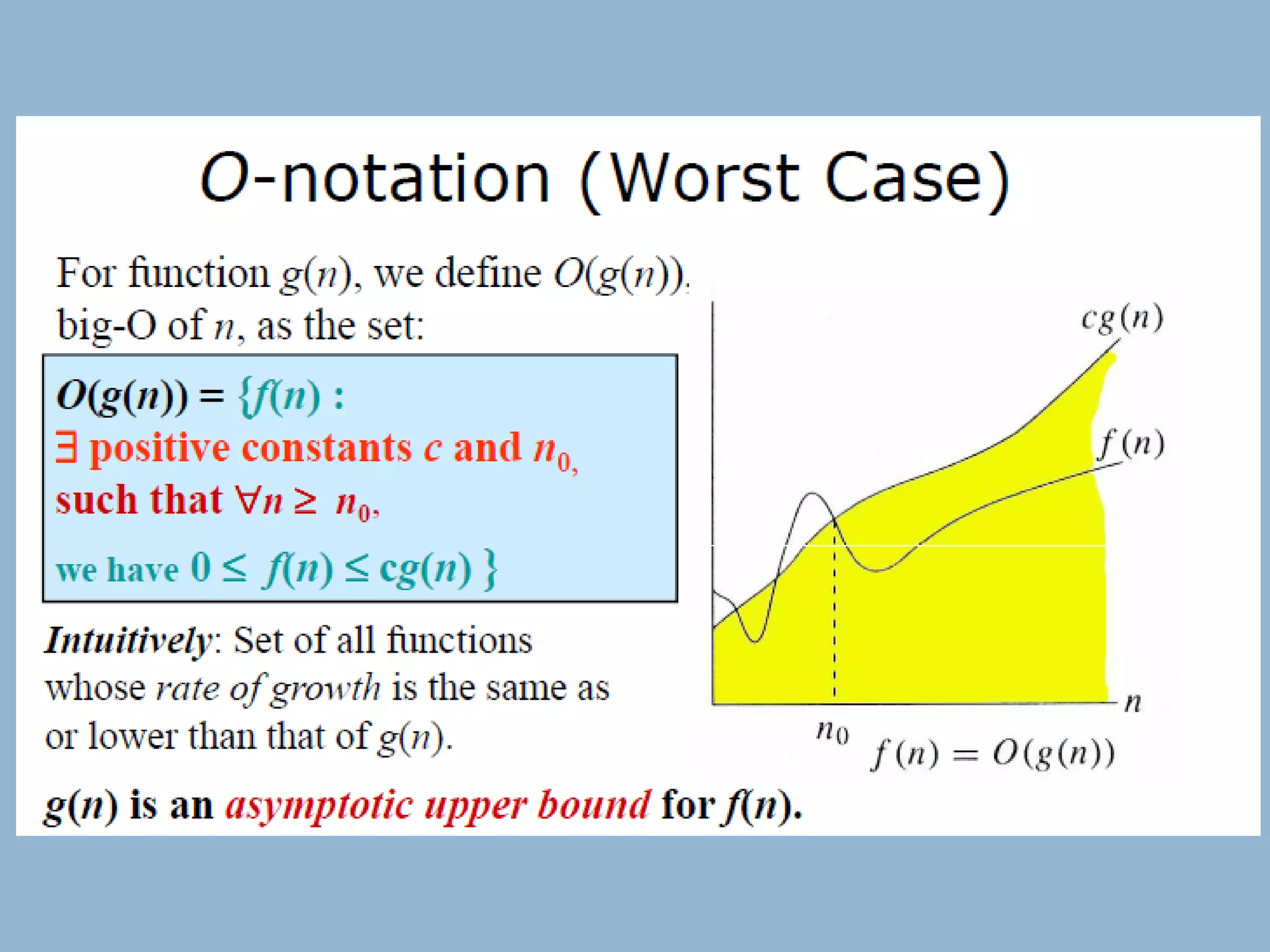
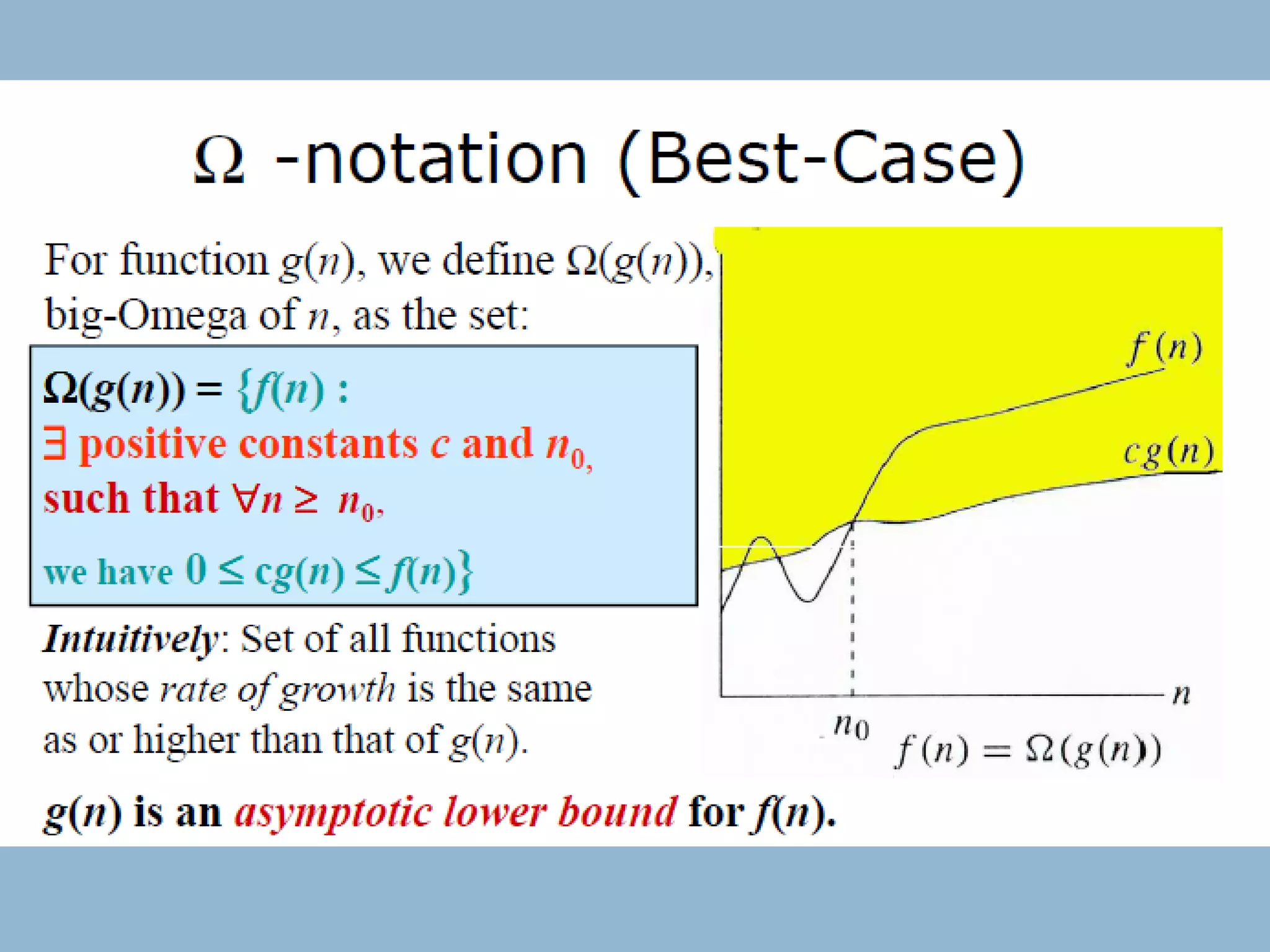
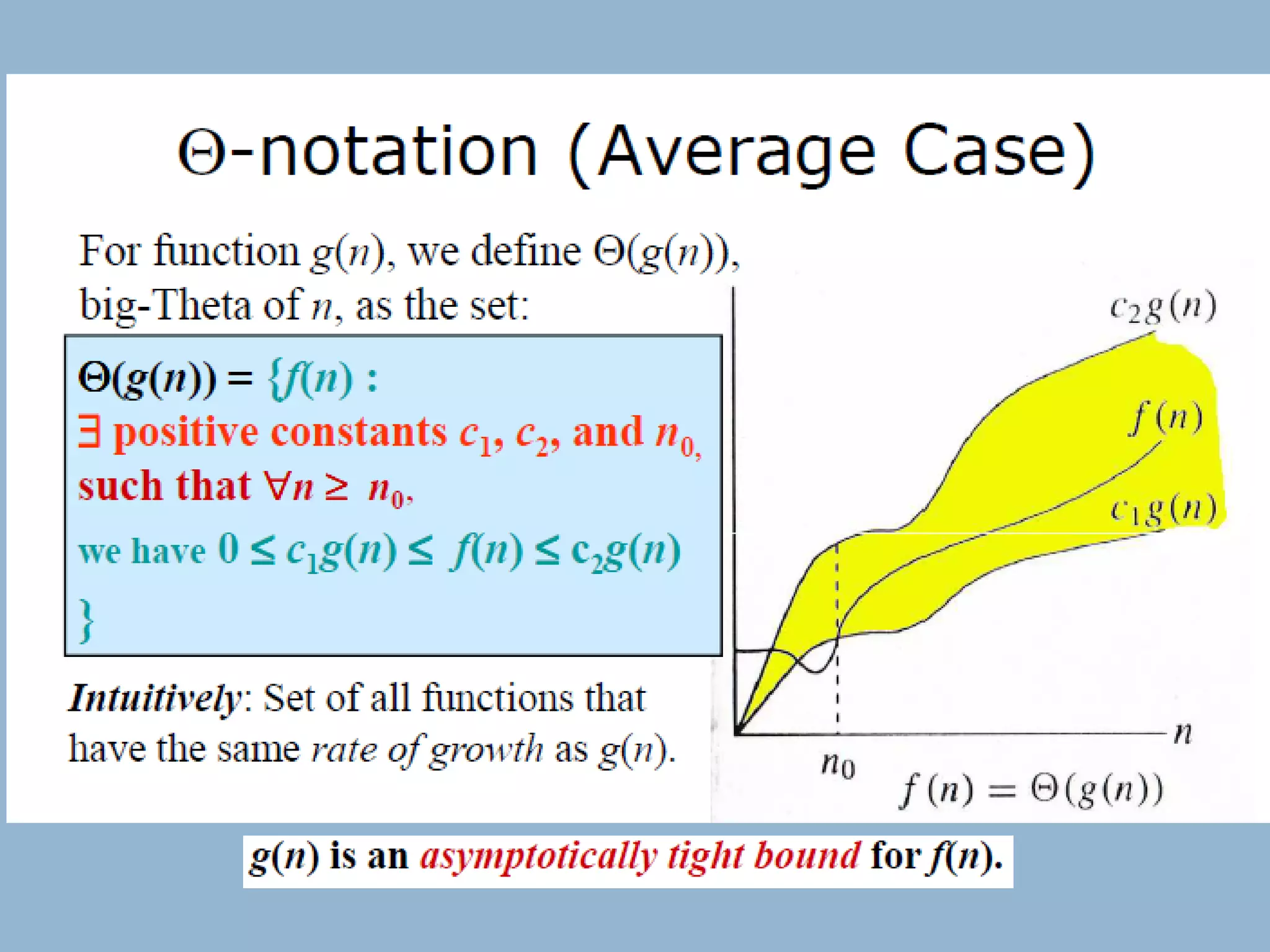
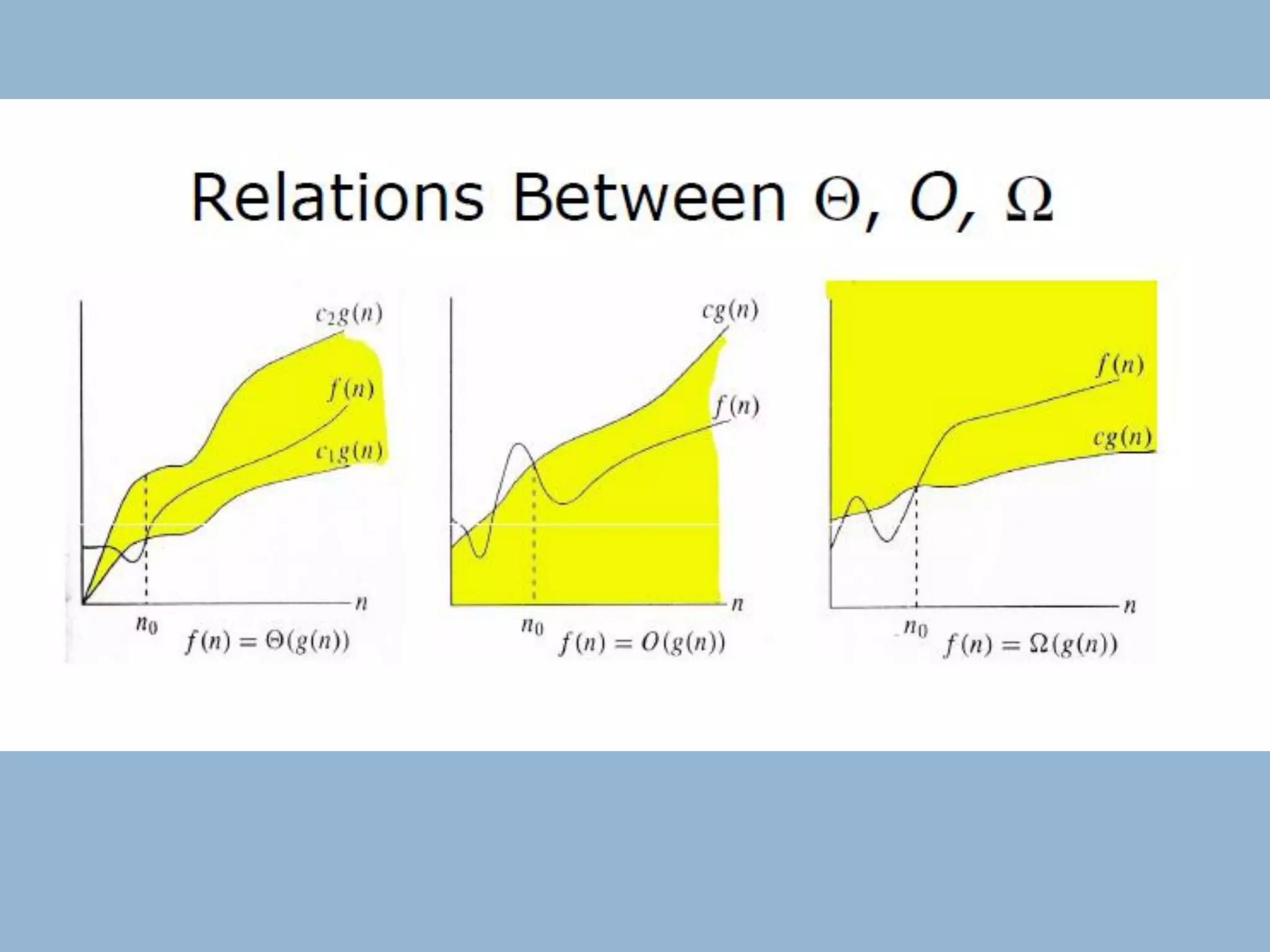
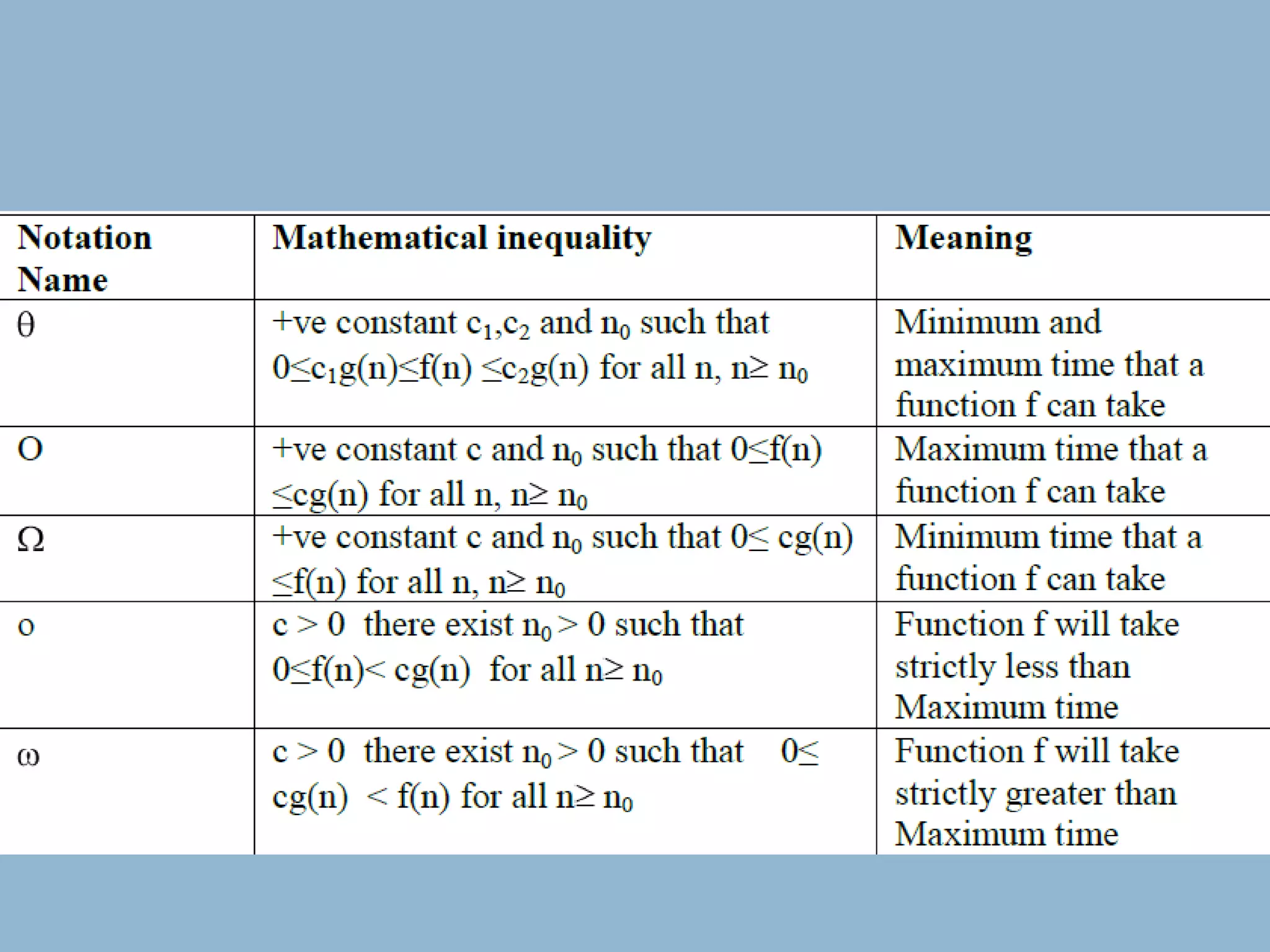
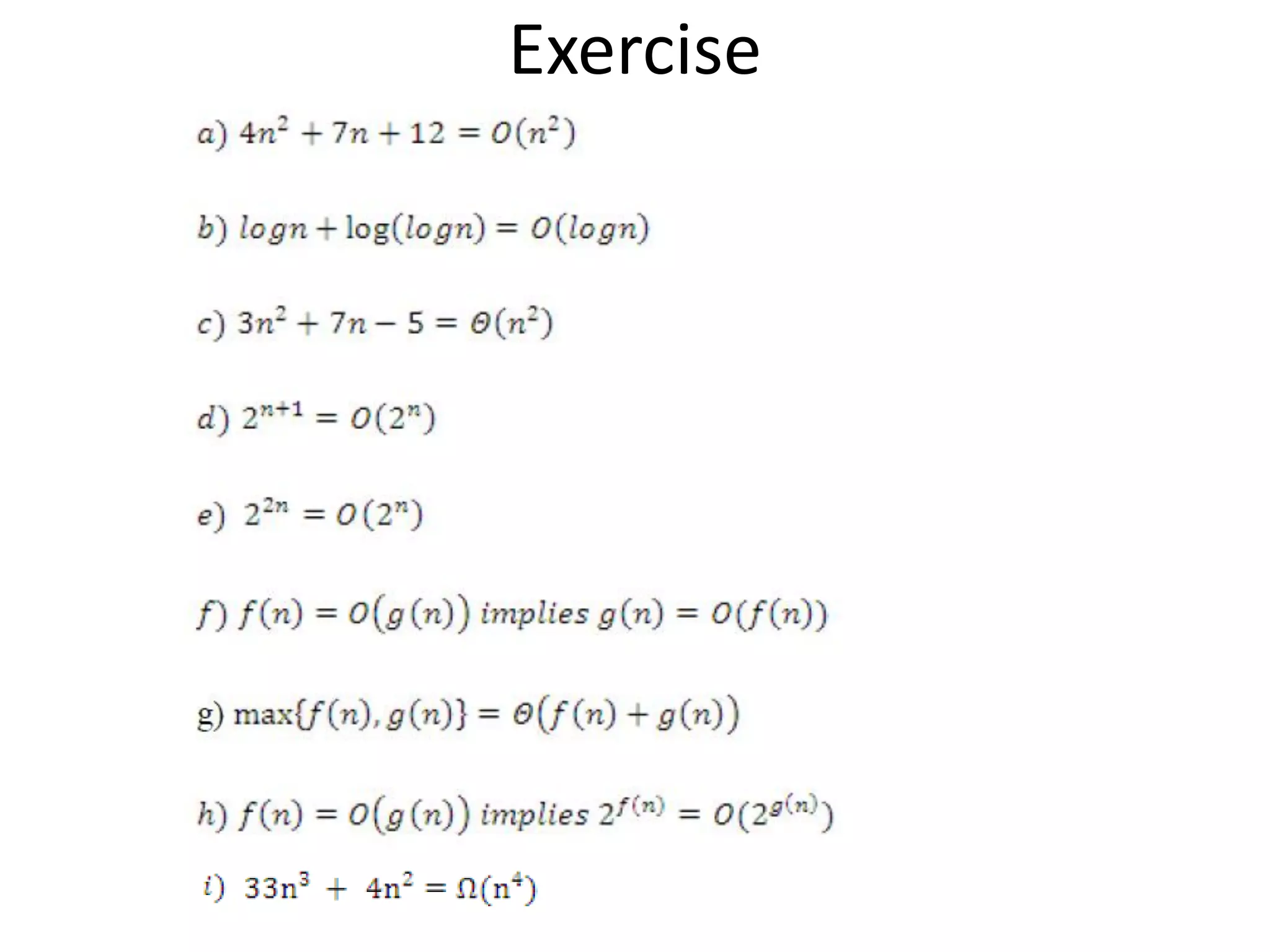This document discusses asymptotic notations and their use in analyzing the time complexity of algorithms. It introduces the Big-O, Big-Omega, and Big-Theta notations for describing the asymptotic upper bound, lower bound, and tight bound of an algorithm's running time. The document explains that asymptotic notations allow algorithms to be compared by ignoring lower-order terms and constants, and focusing on the highest-order term that dominates as the input size increases. Examples are provided to illustrate the different orders of growth and the notations used to describe them.

1. Lecture 4 : Asymptotic Notations
Jayavignesh T
Asst Professor
SENSE

2. How to calculate running time then?
for (i=0; i < n ; i ++) // 1 ; n+1 ; n times
{
for (j=0; j < n ; j ++) // n ; n(n+1) ; n(n)
{
c[i][j] = a[i][j] + b[i][j];
}
}
3n2+4n+ 2 = O(n2)

3. Analysis – Insertion Sort

4. Insertion Sort – Tracing Input

5. Analysis – Insertion Sort
• Assume that the i th line takes time ci , which is a constant.
(Since the third line is a comment, it takes no time.)
• For j = 2, 3, . . . , n, let tj be the number of times that the
while loop test is executed for that value of j .
• Note that when a for or while loop exits in the usual way -
due to the test in the loop header - the test is executed
one time more than the loop body.

6. Analysis – Insertion Sort – Running time

7. Best case Analysis

10. Worst case Analysis

11. Average Case

13. Importance of Constants during Algorithmic
Analysis
• Problem Size gets sufficiently large, lower order
terms and constants do not matter and are dropped
• Two Algorithms may have same Big-Oh Time
Complexity even if one is faster than other
• Algorithm 1 : N2 time
• Algorithm 2 : 10N2 + N
– Both these algorithms time is O(N2) but Alg 1 faster.
• Constants do not matter when algorithm scales?

14. Linear Time vs Quadratic Time
2 Algorithms have different Big-Oh time complexity, constants & lower order terms
matter only when problem size is small.

15. What is Asymptote?
• Provides a behavior in respect of other function for
varying value of input size.
• An asymptote is a line or curve that a graph
approaches but does not intersect.
• An asymptote of a curve is a line in such a way that
distance between curve and line approaches zero
towards large values or infinity.

17. Asymptotic Notations
• Asymptotic notations (as n tends to ∞)
– used to express the running time of an algorithm in terms
of function, whose domain is the set of natural numbers
N={1,2,3,…..}.
• Asymptotic notation gives the rate of growth,
– i.e. performance of the run time for “sufficiently large
input sizes” (as n tends to infinity)
• Easier to predict bounds for the algorithm than to
predict an exact speed.
– Short-hand way to represent fastest possible, slowest
possible running times of algorithm using high and low
bounds on speed.

18. Asymptotic Notations contd..
• O (Big – Oh)
– This notation is used to express Upper bound (maximum
steps) required to solve a problem
– Worst case growth of algorithm
• Ω (Big – Omega)
– To express Lower bound i.e. minimum (at least) steps
required to solve a problem
– Best case growth of algorithm
• Θ (Big - Theta)
– To express both Upper & Lower bound, also called tight
bound
– (i.e. Average case) on a function

19. Asymptotic Order of Growth
• A way of comparing functions that ignores constant
factors and small input sizes
• O(g(n)): class of functions f(n) that grow no faster
than g(n)
• Θ(g(n)): class of functions f(n) that grow at same
rate as g(n)
• Ω(g(n)): class of functions f(n) that grow at least as
fast as g(n)

20. Why are asymptotic notations important?
• They give a simple characterization of an algorithm’s
efficiency.
• They allow the comparison of the performances of
various algorithms.
• For large values of components/inputs, the
multiplicative constants and lower order terms of an
exact running time are dominated by the effects of
the input size (the number of components).

21. Asymptotic – Summary
• A way to describe behavior of functions in the limit.
• Describe growth of functions.
• Focus on what’s important by abstracting away low order
terms and constant factors.
• Indicate running times of algorithms.
• A way to compare “sizes” of functions.
• Examples: – n steps vs. n+5 steps, – n steps vs. n2 steps
• Running time of an algorithm as a function of input size n for
large n.
• Expressed using only the highest-order term in the expression
for the exact running time.

26. Asymptotic Notations..

27. Asymptotic Notations..

29. Problems – Big Oh, Big Omega, Big Thetha
• First two functions are linear and hence have a lower order
of growth than g(n) = n2, while the last one is quadratic and
hence has the same order of growth as n2
• Functions n3 and 0.00001n3 are both cubic and hence have a
higher order of growth than n2, and so has the fourth-
degree polynomial n4 + n + 1

30. Problems – Big Oh, Big Omega, Big Thetha
• Ω(g(n)), stands for the set of all functions with a higher or
same order of growth as g(n) (to within a constant multiple,
as n goes to infinity).
• Θ(g(n)) is the set of all functions that have the same order of
growth as g(n) (to within a constant multiple, as n goes to
infinity). Every quadratic function an2 + bn + c with a > 0 is in
Θ(n2).

31. Exercise