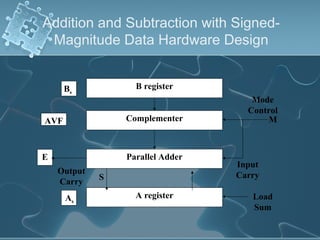
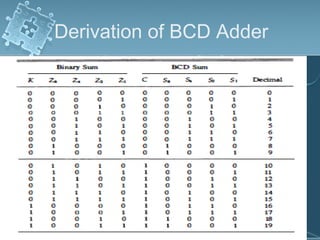
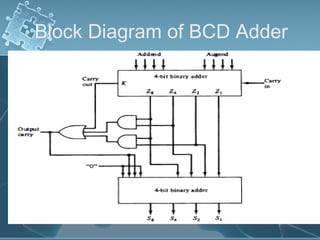
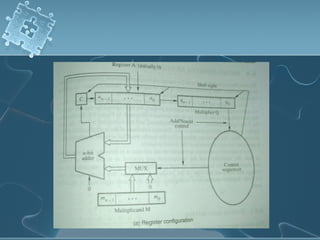
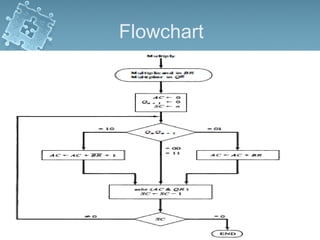
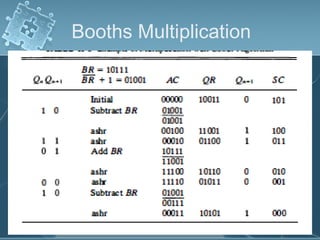
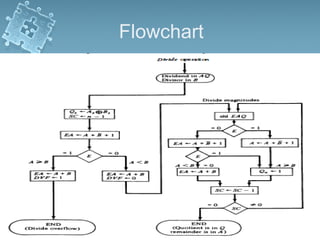
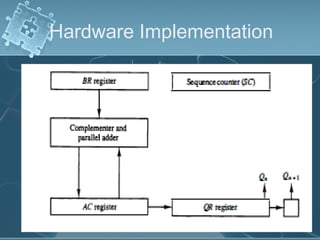
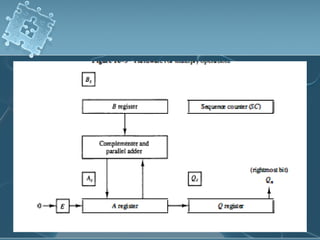
1) There are several algorithms for performing multiplication and division with signed-magnitude numbers, including array multiplication, Booth's multiplication, restoring division, and non-restoring division. 2) Hardware implementations of these algorithms often involve adders, shifters, and correction logic to handle issues like overflow and producing results in the proper number format. 3) Division algorithms in particular require handling issues like division by zero and divide overflow through detection logic and interrupt-driven error handling.

1. Multiplication and Division with
Signed-Magnitude Data
Module II

2. Eight Conditions for Signed-
Magnitude Addition/Subtraction
Operation
ADD
Magnit
udes
SUBTRACT Magnitudes
A > B A < B A = B
(+A) + (+B) + (A + B)
(+A) + (-B) + (A – B ) - (B – A ) + (A – B )
(-A) + (+B) - (A – B ) + (B – A ) + (A – B )
(-A) + (-B) - ( A + B)
(+A) - (+B) + (A – B ) - (B – A ) + (A – B )
(+A) - (-B) + (A + B)
(-A) - (+B) - ( A + B)
(-A) - (-B) - (A – B ) + (B – A ) + (A – B )

3. Examples
Example of adding
two magnitudes
when the result is
the sign of both
operands:
+3 0 011
+ +2 0 010
+5 0 101
Example of adding two
magnitudes when the
result is the sign of
the larger magnitude:
-3 1 011
+ +2 0 010
-( +3
011
- +2) 010

4. Flowchart of Addition and Subtraction
with Signed-Magnitude Data

5. Addition and Subtraction with Signed-
Magnitude Data Hardware Design
A register
AVF
E
Bs
As
B register
Complementer
Parallel Adder
S
Load
Sum
M
Mode
Control
Input
CarryOutput
Carry

6. Summary of Addition and Subtraction
with Signed-Magnitude Data
 The signs use an exclusive OR gate where if
the output is 0, then the signs are the same.
 Hence, add the magnitudes of the same
signed numbers. If the sum is an overflow,
then a carry is stored in E where E = 1 and
transferred to the flip-flop AVF, add-
overflow.
 Otherwise, the signs are opposite and
subtraction is initiated and stored in A.
 No overflow can occur with subtraction so
the AVF is cleared.
 If E = 1, then A > B.
 However, if A = 0, then A = B and the sign is
made positive.
 If E = 0, then A < B and sign for A is

7. BCD Adder
Is a circuit that adds two BCD digits in
parallel and produces the sum in BCD.
Correction logic

8. Derivation of BCD Adder

9. Block Diagram of BCD Adder

10. Correction logic formula
C=1 add 0110 to the binary sum

11. Operation
Decimal digits are added with input
carry with binary adder.
If output carry is zero, nothing is to be
added to the binary sum.
When output carry=1, 0110 is added to
the binary sum through the next adder.
 the next output carry can be ignored..

12. Multiplication
• A complex operation compared with
addition and subtraction
Many algorithms are used, esp. for
large numbers
Simple algorithm is the same long
multiplication taught in grade school —
Compute partial product for each digit
— Add partial products

13. Multiplication Example
 1011 Multiplicand (11 dec)
 x 1101 Multiplier (13 dec)
 1011 Partial products
0000 Note: if multiplier bit is 1 copy
1011 multiplicand (place value)
1011 otherwise zero
10001111 Product (143 dec)
Note: need double length result

14. Multiplication Algorithms

15. looking at successive bits of the multiplier, least
significant bit first.
If the multiplier bit is a 1, the multiplicand is
copied down;
otherwise, zeros are copied down.
The numbers copied down in successive lines
are shifted one position to the left from the
previous number.
Add these numbers.

16. Array Multiplier
Positive numbers can be implemented
in a combinational two-dimensional
array
Main component of each cell is a full
adder FA

19. Array multiplier is well known due to its
regular structure. Multiplier circuit is based
on add and shift algorithm. Each partial
product is generated by the multiplication of
the multiplicand with one multiplier bit. The
partial product are shifted according to their
bit orders and then added. The addition can
be performed with normal carry propagate
adder. N-1 adders are required where N is
the multiplier length

22. Flowchart

24. Booths Multiplication
Algorithms
1. The multiplicand is subtracted from the
partial product upon encountering the first least
significant 1 in a string of 1's in the multiplier.
2. The multiplicand is added to the partial
product upon encountering the first 0 (provided
that there was a previous 1) in a string of O's in
the multiplier.
3. The partial product does not change when
the multiplier bit is identical to the previous
multiplier bit.

25. Hardware Implementation

26. Flowchart

27. Booths Multiplication

28. Division Algorithms

29. Hardware Implementation for
Signed-Magnitude Data for
restoring divioin
Instead of shifting the partial product to
the right,the divisor and partial product
are shifted to the right.
For subtraction, perform 2’s
complemented addition.

31. Algorithms steps
Do the following n times
Shift A and Q left one binary position
Subtract M from A, and place the answer
back in A.(2’s complement addition of
divisor)
If E=1 A>=B set Qn=1.
Quotient bit 1 is added in Qn bit of partial
remainder and that is shifted to the left.

32. If E=0,A<B so the quotient in Qn
remains a 0.
 The value of B is then added to the partial
remainder and is shifted to the left.
Finally, , the quotient is in Q and final
remainder in A.

34. Divide Overflow
Critical when implemented in hardware
The length of the registers is finite and
will not hold a number exceeds its
length.
When the dividend is twice as long as
the divisor, overflow occurs:
If the high-order half bits of the dividend
constitute a number greater than or equal
to the divisor.

35. Division by zero must be avoided.
 detected by DVF(divide overflow
flipflop).

36. Handling Divide Overflow
Duty of the programmer
The occurrence of a divide overflow
stopped the computer (divide stop).
Not recommended(time consuming)
Provide an interrupt request when DVF
is set.
Suspend the current program and branch
to a service routine to take the corrective
actions.

37. Corrective measure:
Remove the program and type an error
message stating the reason.
The best way to avoid divide overflow
is use floating point data.

38. Flowchart