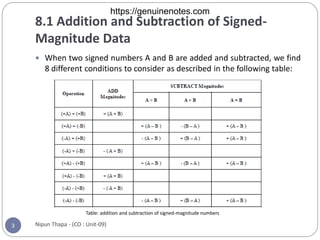
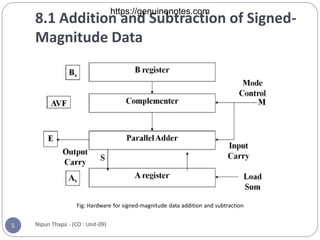
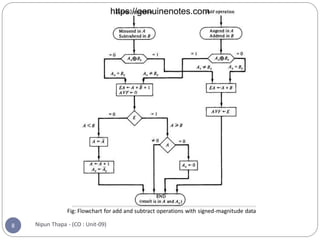
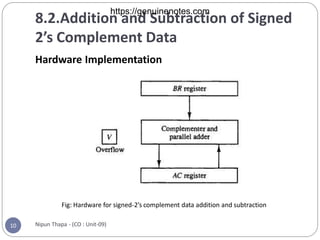
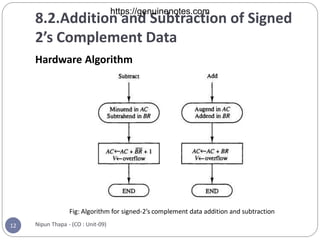
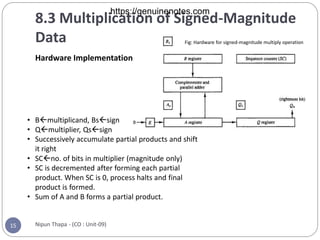
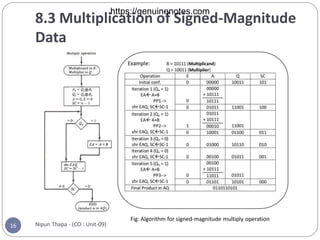
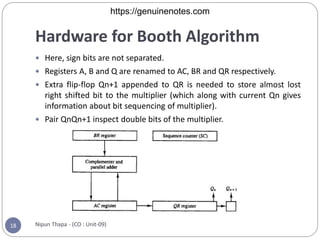
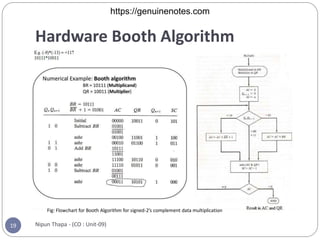
Chapter 8 covers computer arithmetic, focusing on arithmetic operations like addition, subtraction, multiplication, and their representations in signed magnitude and signed 2’s complement forms. It details the algorithms and hardware implementations for performing these operations, highlighting the differences between the two representations and their respective processes. The chapter also introduces the Booth multiplication algorithm for signed 2’s complement data, which optimizes multiplication through a specific set of rules.