Unsharp masking (USM) is an image processing technique that enhances detail by increasing edge contrast through a high-pass filter. The adaptive unsharp masking approach aims to minimize overshoot artifacts by emphasizing medium-contrast details while being robust against noise in smooth areas. This method uses an iterative adaptation algorithm to optimize scaling factors for correction signals, improving local dynamics in images.

1. ADAPTIVE UNSHARP MASKING
Digital Image Processing

2. Contents
• What is Unsharp Masking..?
• Concept of Operation
• Drawbacks
• Adaption Algorithm
• Advantages of Unsharp Masking

3. Unsharp Masking
• Unsharp masking (USM) is an image manipulation
technique.
• An unsharp mask cannot create additional detail, but it can
greatly enhance the appearance of detail by increasing
small-scale acutance (the edge contrast of an image).
• Normally an "unsharp mask" is used to sharpen an image
which can help us to emphasize texture and detail of the
image.

4. Concept of Operation
• Normally in Unsharp Masking, a highpass filtered, scaled
version of an image is added to the image itself.
• This will improve the visual appearance of an image
significantly by emphasizing its high frequency contents to
enhance the edge and detail information in it.
• Generally an unsharp mask is a filter that amplifies high-
frequency components.

5. • The enhanced image y(n,m) is obtained from the input
image x(n,m) as
y(n,m) = x(n,m) + ƛz(n,m)
• where z(n,m) is the correction signal computed as the
output of a linear high pass filter.
• ƛ is the positive scaling factor that controls the level of
contrast enhancement achieved at the output.

6. hx hy
0 -1 0 0 0 0
0 2 0 -1 2 -1
0 -1 0 0 0 0
Zx=conv(x,hx) Zy=conv(x,hy)
z(n,m) = [zx(n,m), zy(n,m)]T
y(n,m) = x(n,m) + ƛz(n,m)

7. Zx Zy
Original Image(x) Output Image(y)

8. Drawbacks
• Even though this method is simple and works well in many
applications, it suffers from two main drawbacks.
i) The presence of the linear high pass filter makes the system
extremely sensitive to noise. This results in perceivable and
undesirable distortions in the images.
ii) It enhances high-contrast areas much more than areas that
do not exhibit high image dynamics. Consequently, some
unpleasant overshoot artifacts may appear in the output
image.

9. Adaptive Unsharp Masking
• In this approach, we introduce a variation of the basic
Unsharp Masking scheme that contains an adaptive filter in
the correction path.
• The objective of the adaptive filter is to emphasize the
medium-contrast details in the input image more than large-
contrast details such as abrupt edges so as to avoid overshoot
effects in the output image.
• The adaptive filter does not perform a sharpening operation
in smooth areas, and therefore the overall system is more
robust to the presence of noise in the input images than
traditional approaches.

10. Implementation diagram

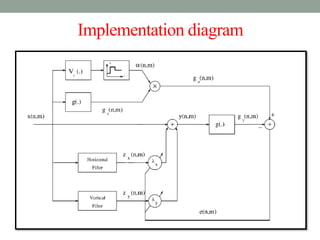
11. Here we go with the approach as below :
y(n,m) = x(n,m) + ƛz(n,m)
where ƛ is the positive scaling factor that controls the level of
contrast enhancement achieved at the output.
ƛ (n,m) = [ƛx(n,m), ƛy(n,m)]T
y(n,m) =x(n,m) + ƛx(n,m)zx(n,m)+ ƛy(n,m)zy(n, m)

12. Objective of this approach
• In the previous equation, ƛx(n,m) and ƛy (n,m) are the
scaling factors for the two components of the correction
signal at the (n,m)th pixel.
• Our objective is to recursively update these parameters
using an adaptation algorithm so as to produce an output
image whose local dynamics are increased in the detail
areas and left unchanged in the uniform areas.
• i,.e., little or no enhancement is applied in smooth areas of
the image, maximum enhancement is applied in medium
contrast areas, and large contrast areas are only moderately
enhanced.

13. Local dynamics
• To determine this classification, we first measure the local
dynamics of the image.
• The local variance computed over a 3 × 3 pixel block is
given by :

14. •
g
-1 -1 -1
-1 8 -1
-1 -1 -1

15. •

16. Adaption Algorithm
•

17. • This process is iteratively repeated until we acquire the
‘error(e)’ in the desired range.
• When the desired range of error is achieved, we stop the
procedure and display the image y which is defined as
y(n,m) =x(n,m) + ƛx(n,m)zx(n,m)+ ƛy(n,m)zy(n, m)
Original Unsharped Image

18. Advantages of Unsharp Masking
• Enhanced apparent sharpness through “edge effects”.
• An important advantage of unsharp masking is that it
increases the sharpness of the prints.
• Reduction of contrast on negatives of excessive contrast.
• Improved print shadow detail.
• Well known benefits in the printing and graphics arts
industries.

19. References:
• http://www.ieee.org
• Andrea Polesel, Giovanni Ramponi, and V. John Mathews
“Image Enhancement via Adaptive Unsharp Masking”, IEEE
TRANSACTIONS ON IMAGE PROCESSING
• Google Images
• MATLAB images

20. THANK YOU