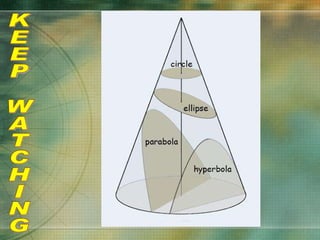
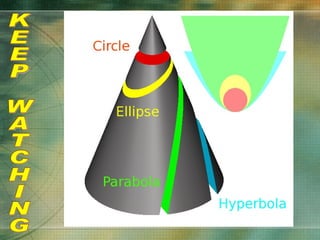
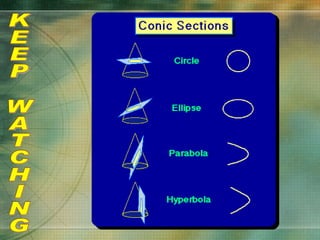
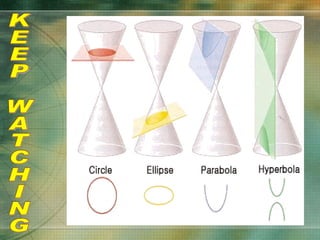
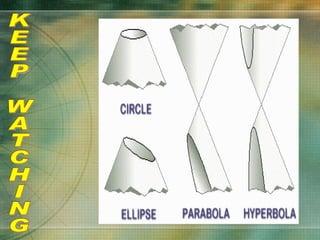
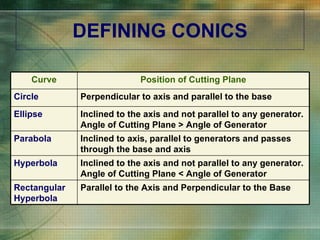
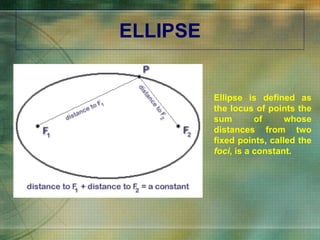
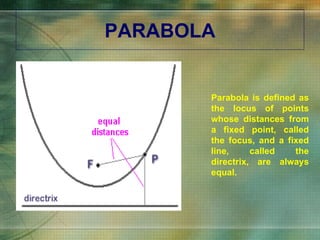
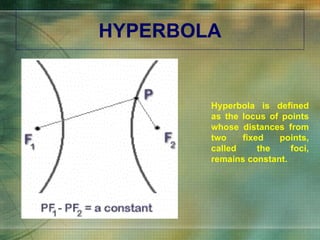
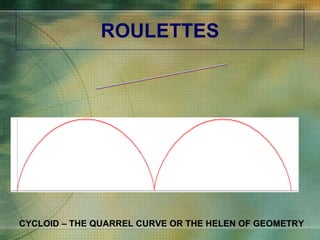
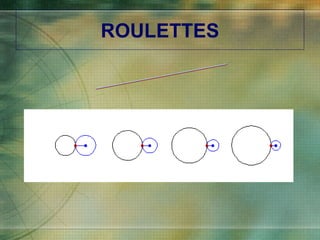
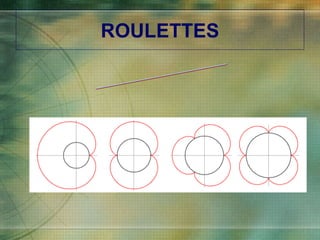
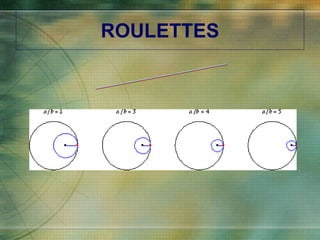
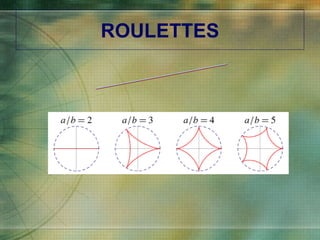
The document discusses various types of curves that are important in engineering applications. It covers conic sections like ellipses, parabolas and hyperbolas. It also discusses roulettes like cycloids and trochoids that are generated by a point on a moving circle. Involutes, which are curves traced by a point unwinding from a circle, are also covered. Examples are provided of how these curves are used in civil, mechanical and electrical engineering applications.

1. CURVES IN ENGINEERING An attempt on lucidity & holism PON.RATHNAVEL

2. Syllabus Conics – Construction of ellipse, Parabola and hyperbola by eccentricity method – Construction of cycloid and involutes of square and circle – Drawing of tangents and normal to the above curves. 10 hours Synopsis Introduction to Curves – Classification of Curves – Introduction to Conics, Roulettes and Involutes Terminology in Curves - Properties of Conics, Roulettes and Involutes - Construction of ellipse by eccentricity method - Construction of Parabola by eccentricity method - Construction of hyperbola by eccentricity method – Construction of cycloid – Construction of Involute of square – Construction of Involute of Circle 05 periods

3. WHY CURVES? CIVIL ENGINEERING Bridges, Arches, Dams, Roads, Manholes etc. MECHANICAL ENGINEERING Gear Teeth, Reflector Lights, Centrifugal Pumps etc ECE Design of Satellites, Missiles etc, Dish Antennas, ECG & EEG Machines CSE & IT Computer Graphics, Networking Concepts ENGINEERING GRAPHICS EXAM 2 Marks - 4 & 15 Marks - 1

4. JUMBLE ? U O L C S

5. LOCUS SET OF POINTS GIVEN CONDITIONS PATH Vs LOCUS Locus is a collection of points which share a property. It is used to define curves in a geometry.

6. CURVE A curve is considered to be the locus of a set of points that satisfy an algebraic equation

8. STICKING TO SYLLABUS Theory CONICS ROULETTES INVOLUTES Practical ELLIPSE PARABOLA HYPERBOLA CYCLOID INVOLUTE OF SQUARE INVOLUTE OF CIRCLE

10. KEEP WATCHING

11. KEEP WATCHING

12. KEEP WATCHING

13. KEEP WATCHING

14. KEEP WATCHING

15. DEFINING CONICS Parallel to the Axis and Perpendicular to the Base Rectangular Hyperbola Inclined to the axis and not parallel to any generator. Angle of Cutting Plane < Angle of Generator Hyperbola Inclined to axis, parallel to generators and passes through the base and axis Parabola Inclined to the axis and not parallel to any generator. Angle of Cutting Plane > Angle of Generator Ellipse Perpendicular to axis and parallel to the base Circle Position of Cutting Plane Curve

16. ELLIPSE Ellipse is defined as the locus of points the sum of whose distances from two fixed points, called the foci , is a constant.

17. PARABOLA Parabola is defined as the locus of points whose distances from a fixed point, called the focus, and a fixed line, called the directrix, are always equal.

18. HYPERBOLA Hyperbola is defined as the locus of points whose distances from two fixed points, called the foci, remains constant.

19. ROULETTES A cycloid is a curve generated by a point on the circumference of a circle as the circle rolls along a straight line without slipping. The rolling circle is called generating circle and the line along which it rolls is called base line or directing line. CYCLOID

20. ROULETTES CYCLOID CYCLOID – THE QUARREL CURVE OR THE HELEN OF GEOMETRY

21. ROULETTES CYCLOID CYCLOID – THE QUARREL CURVE OR THE HELEN OF GEOMETRY

22. ROULETTES An epicycloid is a curve generated by a point on the circumference of a circle which rolls on the outside of another circle without sliding or slipping. The rolling circle is called generating circle and the outside circle on which it rolls is called the directing circle or the base circle. EPICYCLOID

23. ROULETTES EPICYCLOID

24. ROULETTES EPICYCLOID

25. ROULETTES A hypocycloid is a curve generated by a point on the circumference of a circle which rolls on the inside of another circle without sliding or slipping. The rolling circle is called generating circle/hypocircle and the inside circle on which it rolls is called the directing circle or the base circle. HYPOCYCLOID

26. ROULETTES HYPOCYCLOID

27. ROULETTES HYPOCYCLOID

28. ROULETTES A trochoid is a curve generated by a point either inside or outside the circumference of a circle that rolls along a straight line without slipping. When the point is inside the circumference of the circle, it is called inferior trochoid. If it is outside the circumference of the circle, it is called superior trochoid. An inferior trochoid is also called prolate cycloid. A superior trochoid is also called curtate cycloid. TROCHOID

29. ROULETTES EPITROCHOID An epitrochoid is a curve generated by a point either inside or outside the circumference of a circle that rolls along the outside of an circle without slipping. When the point is inside the circumference of the circle, it is called inferior epitrochoid. If it is outside the circumference of the circle, it is called superior epitrochoid.

30. ROULETTES HYPOTROCHOID A hypotrochoid is a curve generated by a point either inside or outside the circumference of a circle that rolls along the outside of an circle without slipping. When the point is inside the circumference of the circle, it is called inferior hypotrochoid. If it is outside the circumference of the circle, it is called superior hypotrochoid.

31. INVOLUTES An involute is a curve traced by a point as it unwinds from around a circle or polygon. The concerned circle or polygon is called as evolute.

32. INVOLUTES

33. INVOLUTES

34. INVOLUTES