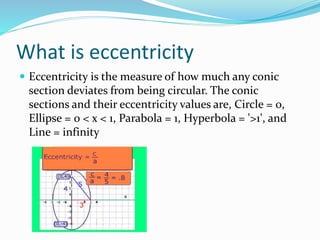
This document discusses various geometric shapes and concepts. It defines angles, polygons, involutes, ellipses, hyperbolas, parabolas, directrix, foci, and eccentricity. Some key points covered include: angles are formed by two rays with a common endpoint; there are four types of angles; polygons are plane figures formed by straight line segments that form a closed chain; involutes are curves traced by unwinding a thread from a circle or polygon; ellipses and hyperbolas are conic sections formed by intersecting a plane with a cone; parabolas are curves formed when a plane is parallel to a cone's side; directrix is the base line of different curves; foci are points related

1. Naumaan Anees
Sarmad Tufail
Talha Ali
Waseem Akram
 Muhammad Asad
Ansub Azeem

2. What is an ANGLE
 ANGLE:
In planar geometry, an angle is the figure formed by
two rays, called the sides of the angle, sharing a
common endpoint, called the vertex of the angle.
Angles formed by two rays lie in a plane

3. Types Of Angle
 Acute Angle:
The acute angle is the small angle which is less than 90°.
 Right Angle:
The angle equal to 90° is right angle.

4.  Obtuse Angle:
The obtuse angle is the smaller angle. It is more than
90° and less than 180°.
 Reflex Angle:
The reflex angle is the larger angle. It is more than 180°
but less than 360°.

5. What are Polygons
 In elementary geometry, a polygon is a plane 2d figure
that is bounded by a finite chain of straight line
segments closing in a loop to form a closed chain.

6. Use of polygons in Drawing
 Hexagonal Nut Head:
The drawing of hexagonal nut is drawn with the help
of hexagon.
 L-N Key Head:
The drawing of inside groove of head of
L-N key is made through
hexagonal construction

7.  White House Pentagon:
The mechanical structure of pentagon, Washington
DC is also made with the help of polygonal shape
pentagon.

8. What is Involute
 Involute :
An Involute is a curve traced by the free end of a thread
unwound from a circle or a polygon in such a way that
the thread is always tight and tangential to the figure.

9. Involute of a circle
The path or loci traced of an unwinding
taut or cord from a circle is called an
involute of a circle.

10. Uses of Involute
The involute has some properties that makes it
extremely important to the gear industry: If two
intermeshed gears have teeth with the profile-shape
of involutes they form an involute gear system.
Their relative rates of rotation are constant while
the teeth are engaged, and also, the gears always
make contact along a single steady line of force.

11. What is an Ellipse
an ellipse is a curve on a plane that surrounds two focal
points such that the sum of the distances to the two
focal points is constant for every point on the curve.
The length of minor axis is less than Length of Major
Axis.

12. Use Of Ellipse In Drawing
 The equation of an ellipse whose major and minor axes
coincide with the Cartesian axes is

13. Use of Ellipse In Drawing
It is use to make geometry of glasses of spectacles.
It is use to show circle on any view in an isometric
diagram.
It is also use to show a circle from a side view.

14. What is Hyperbola
 If we cut side of cone except from centre along vertical
axis than a hyperbolic curve is obtained.
• A symmetrical open curve formed by the
intersection of a circular cone with a plane at
a smaller angle with its axis than the side of the
cone.

16. Use of hyperbola in drawing
 In construction of Nuclear Reactor Walls.

17. What is Parabola
 A symmetrical open plane curve formed by the
intersection of a cone with a plane parallel to its side.
The path of a projectile under the influence of gravity
ideally follows

18. Uses of parabola in drawing
 It is use to make Mega structures of large Bridges as
they make parabolic curves for bearing load.

19. What is Directrix
 A directrix is the base line of any curve it may be
hyperbolic, parabolic, circle and ellipse.
 A directrix is a line on which maxima, minima or point
of intersection lies.

21. Directrix in parabola
 A parabola is set of all points in a plane which are an
equal distance away from a given point and given line.
The point is called the focus of the parabola, and the
line is called the directrix.
 The directrix is perpendicular to the axis of symmetry
of a parabola and does not touch the parabola. If the
axis of symmetry of a parabola is vertical, the directrix
is a horizontal line.
 If we consider only parabolas that open upwards or
downwards, then the directrix is a horizontal line of
the form y = c .

22. Relation between focus vertex and
directrix
 The vertex of the parabola is at equal distance between
focus and the directrix.
 If F is the focus of the parabola, V is the vertex and D is
the intersection point of the directrix and the axis of
symmetry, then V is the midpoint of the line segment .
.

23. Calculation of Directrix

24. What Is Foci
 Foci is a point having the property that the distances
from any point on a curve to it and to a fixed line have
a constant ratio for all points on the curve.

25. Foci of ellipse
 An ellipse has two focus points.
 The foci always lie on the major (longest) axis, spaced
equally each side of the center. If the major axis and
minor axis are the same length, the figure is a circle
and both foci are at the center. Reshape the ellipse
above and try to create this situation.

26. Calculation of foci
 if you have an ellipse with known major and minor axis
lengths, you can find the location of the foci using the
formula below.
 where F is the distance from each focus to the center
(see figure above)
 j is the semi-major axis (major radius)
 n is the semi-minor axis (minor radius)

27. What is eccentricity
 Eccentricity is the measure of how much any conic
section deviates from being circular. The conic
sections and their eccentricity values are, Circle = 0,
Ellipse = 0 < x < 1, Parabola = 1, Hyperbola = '>1', and
Line = infinity

28. Eccentricity in ellipse
 The eccentricity of an ellipse is a measure of how
nearly circular the ellipse. Eccentricity is found by the
following formula eccentricity = c/a where c is the
distance from the center to the focus of the ellipse a is
the distance from the center to a vertex

29. Calculation of Eccentricity
 The eccentricity is calculated by the formula given as
 where
c is the distance from the center to a focus.
a is the distance from that focus to a vertex