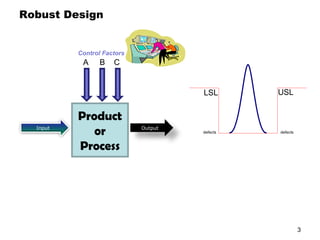
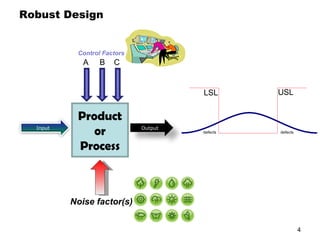
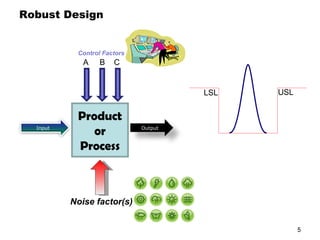
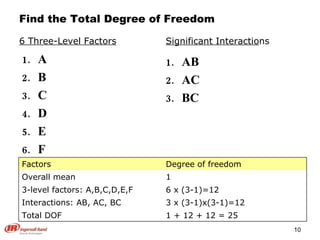
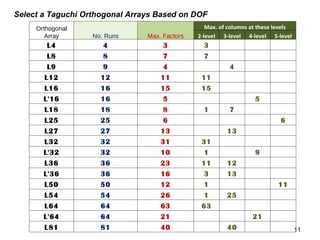
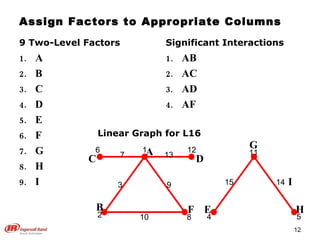
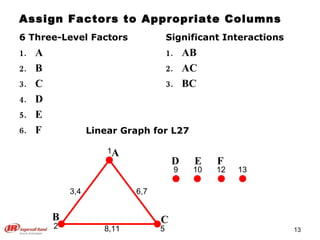
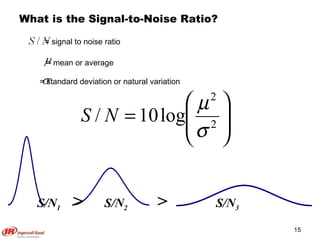
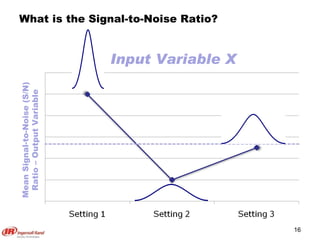
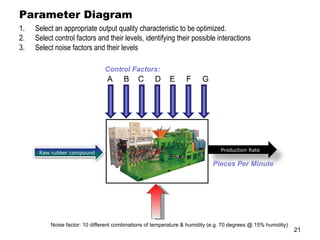
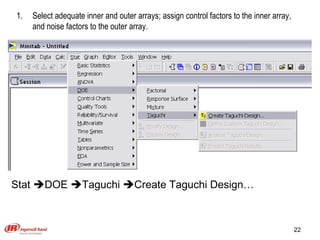
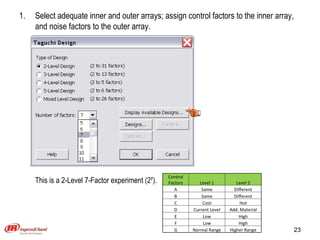
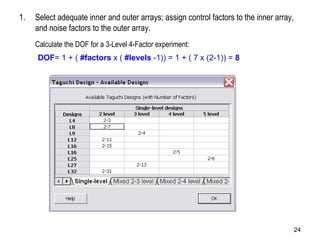
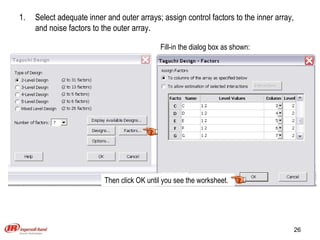
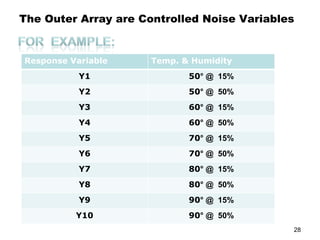
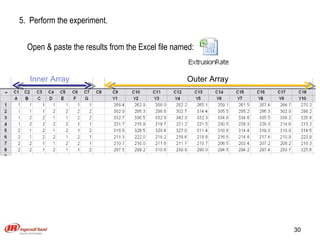
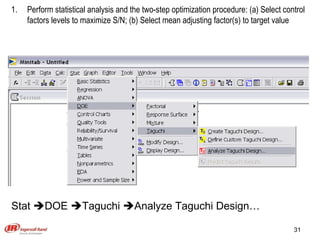
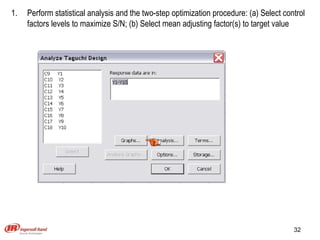
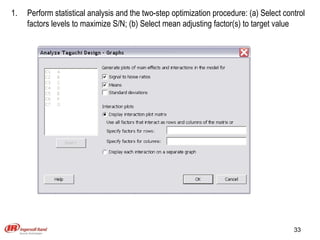
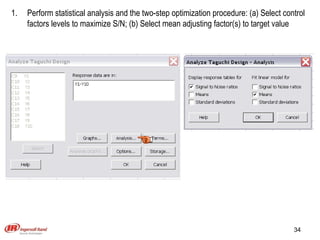
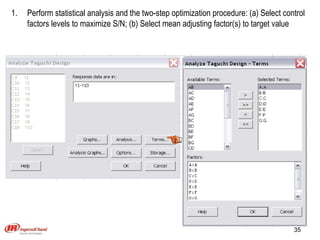
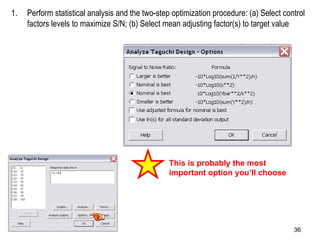
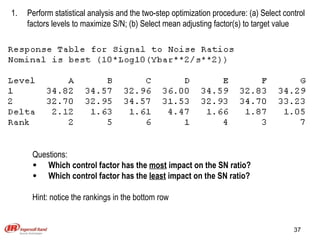
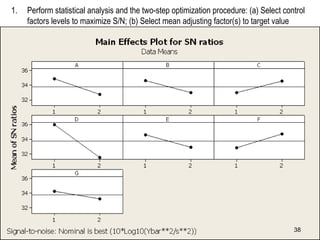
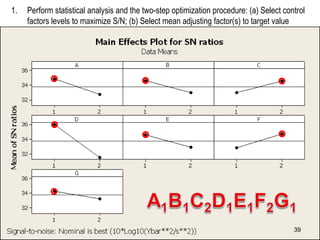
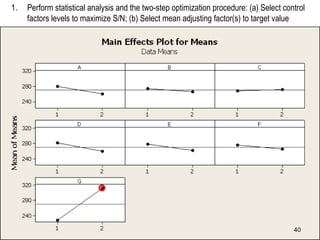
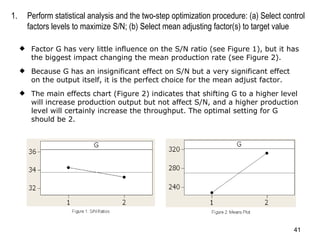
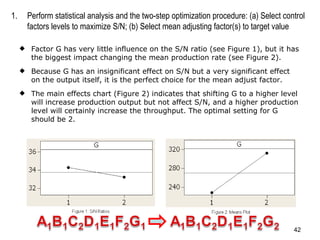
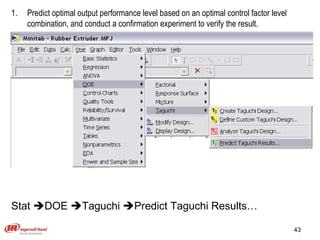
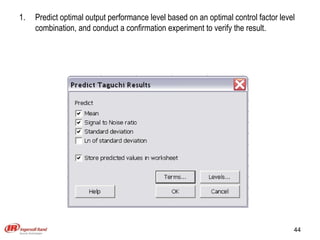
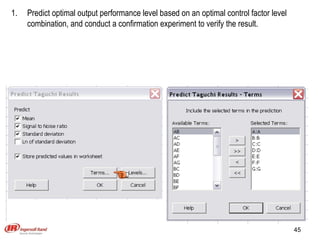
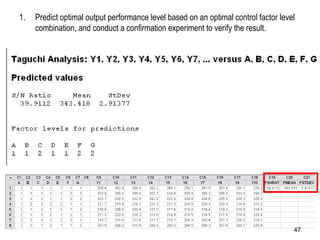
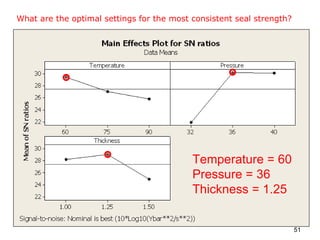
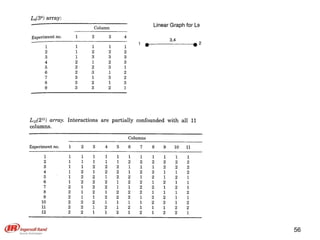
The document discusses Taguchi methods for robust design, focusing on experimental design strategies introduced by Dr. Genichi Taguchi, including the use of orthogonal arrays and signal-to-noise ratios. It outlines a structured approach for selecting factors and their levels, considering noise influences, and emphasizes maximizing quality by minimizing output variation. The document also provides an application example in the rubber industry and a class exercise involving seal strength of plastic bags.