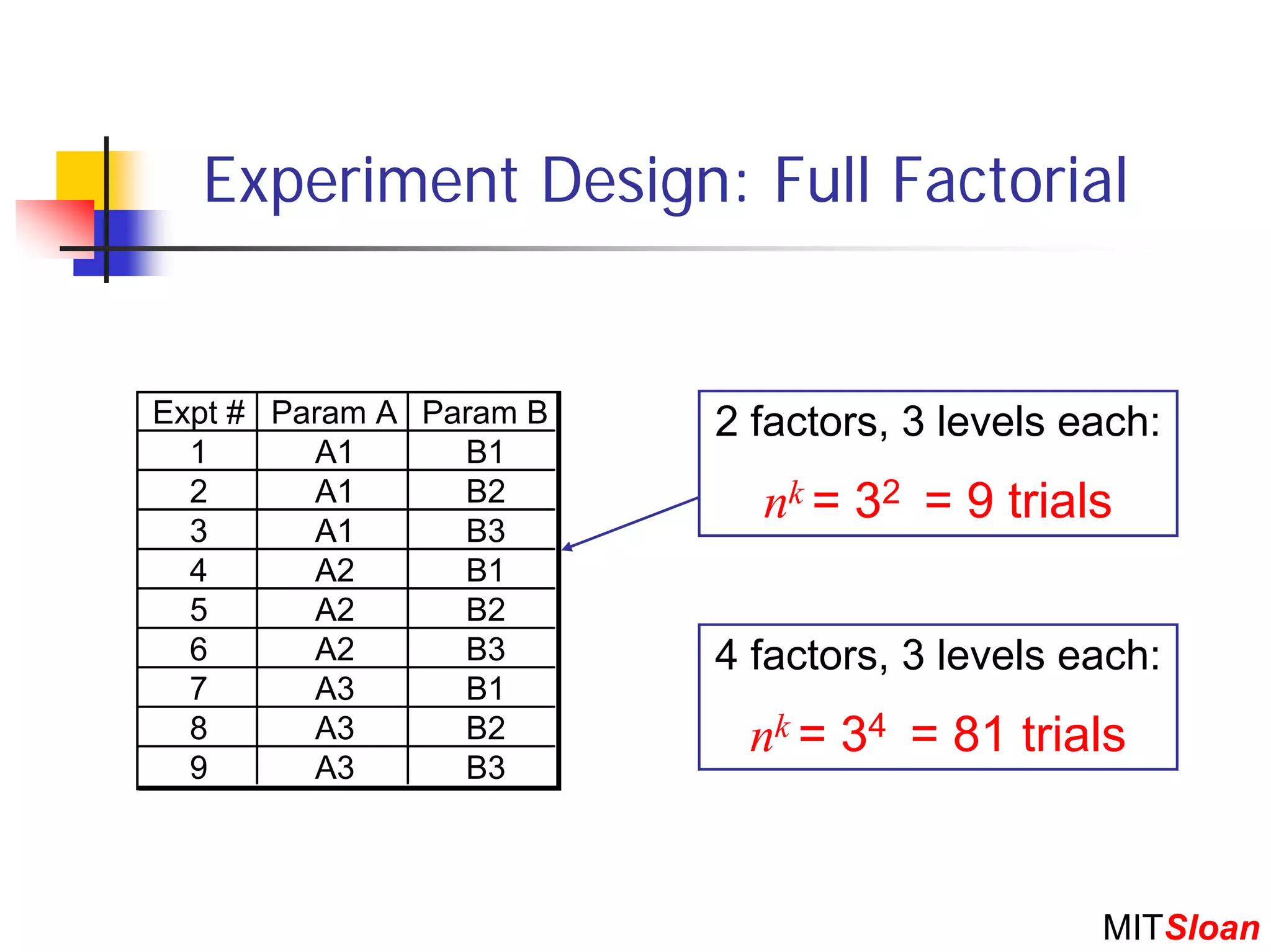
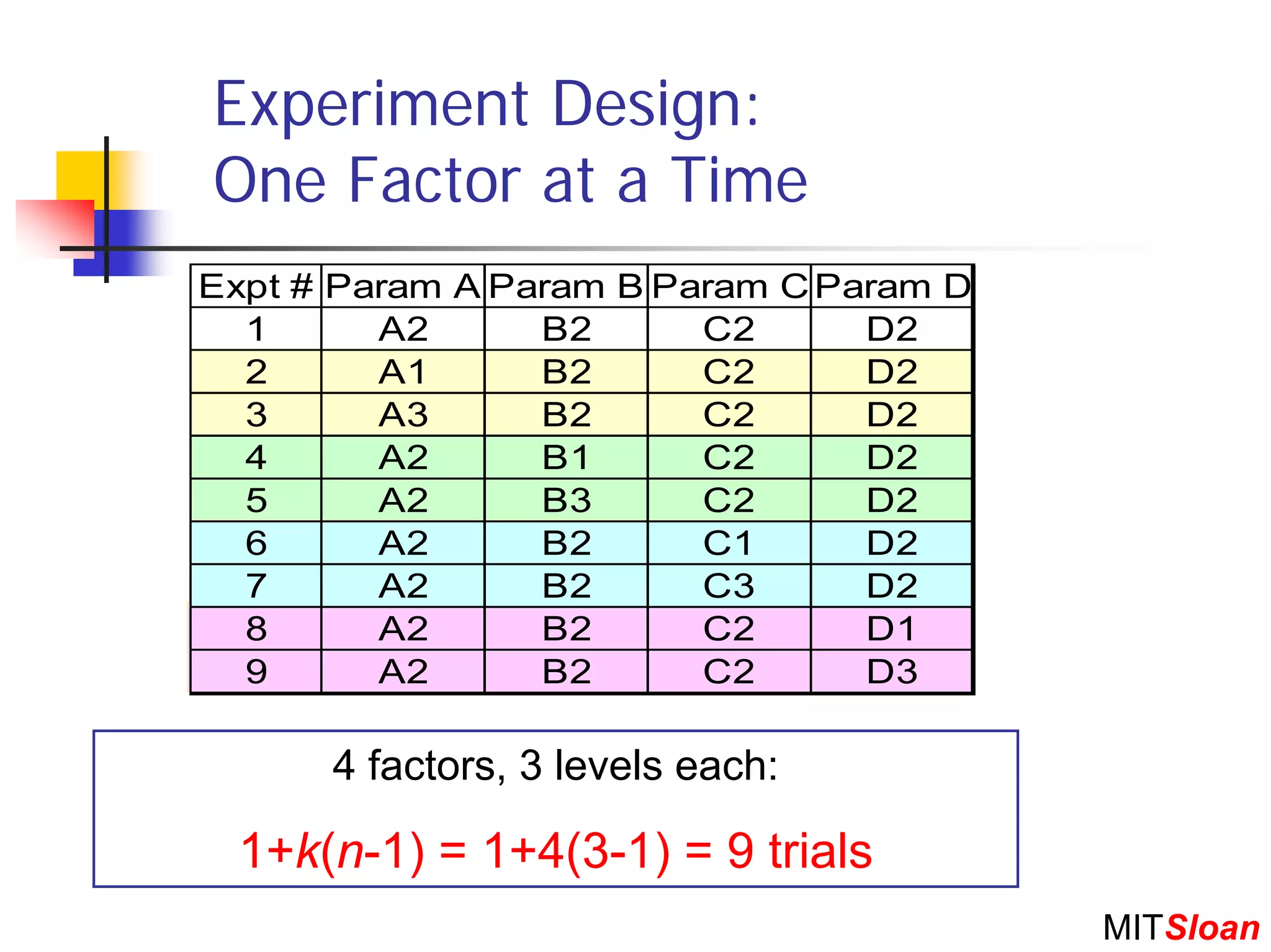
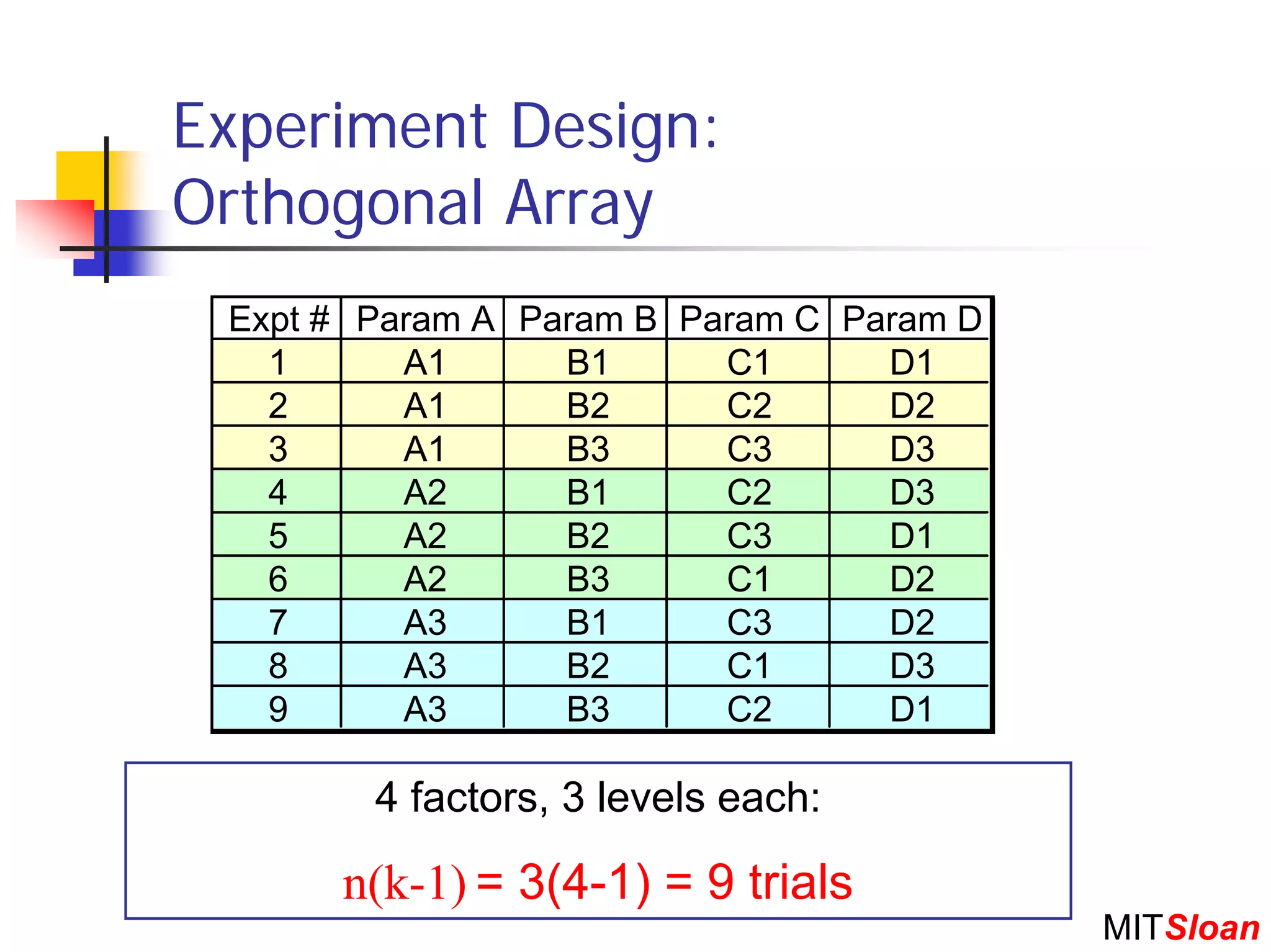
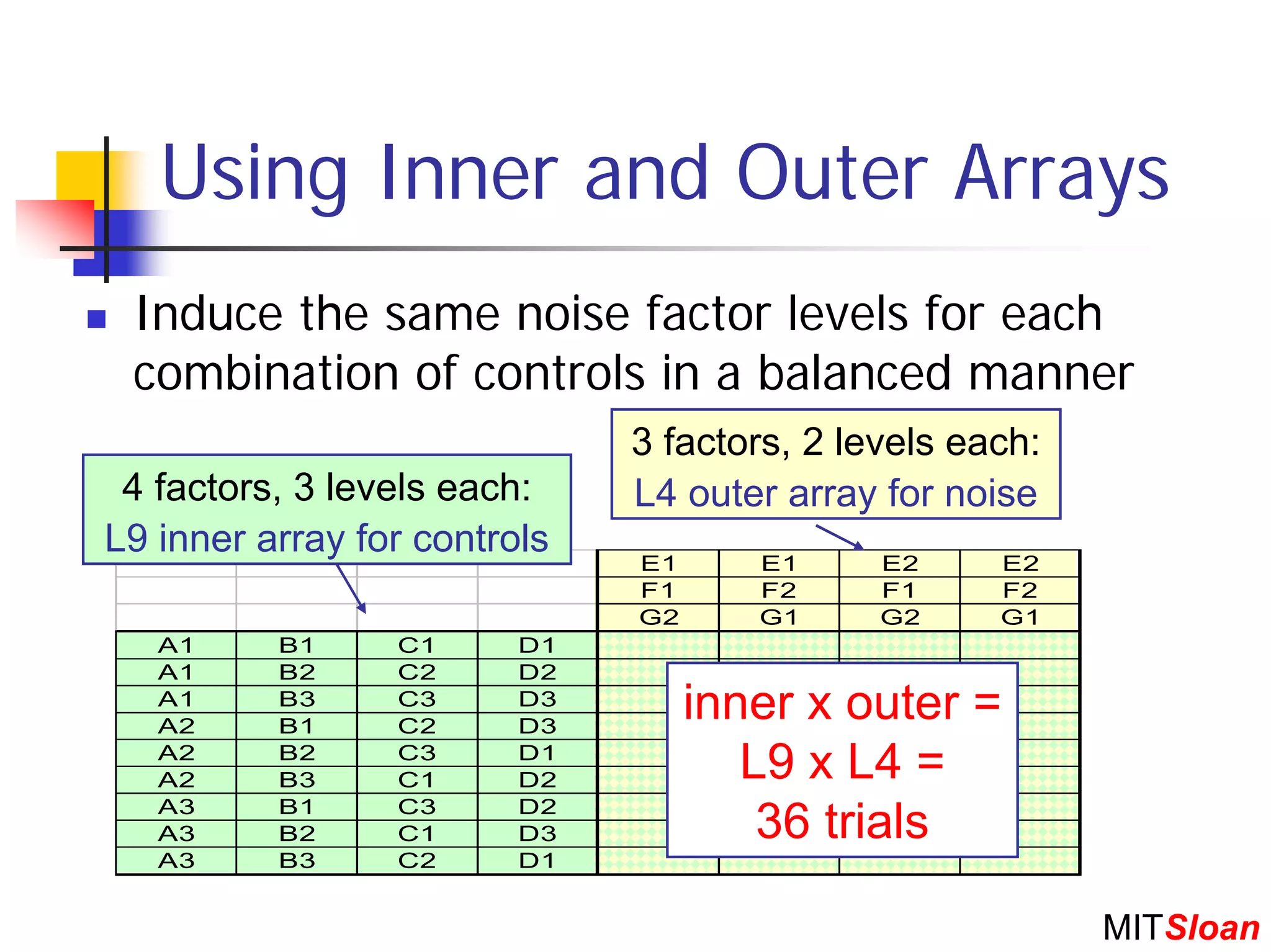
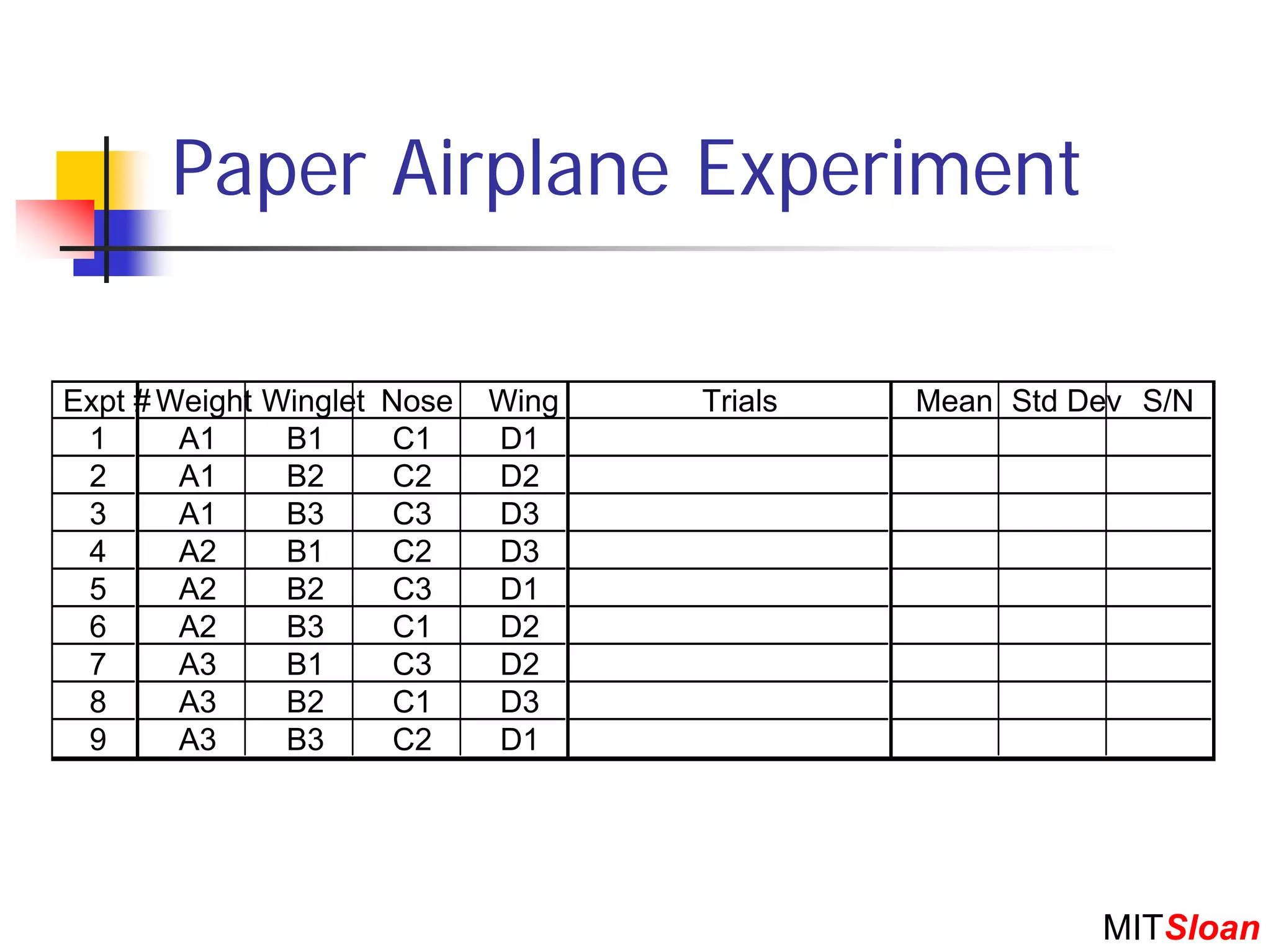
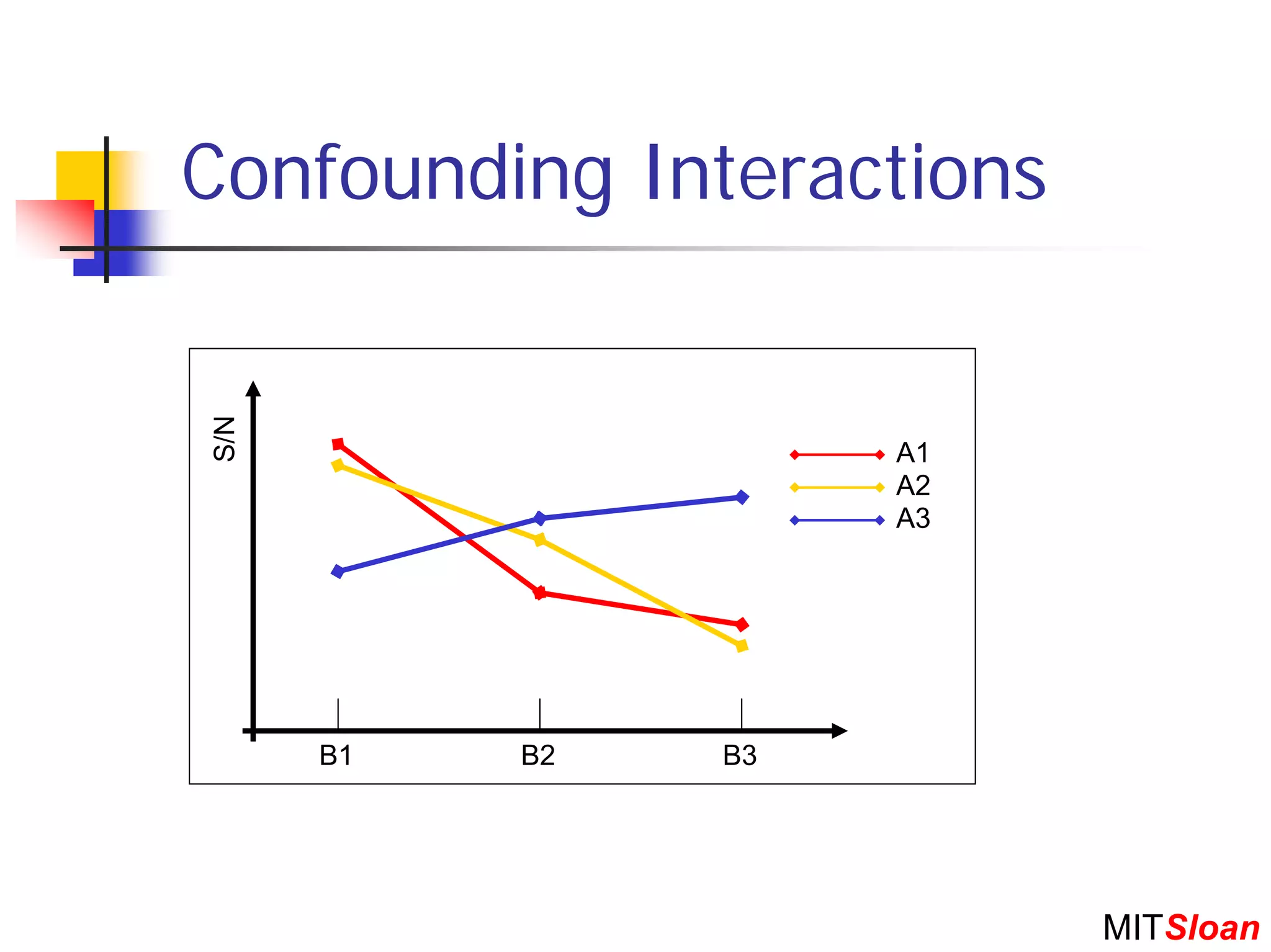
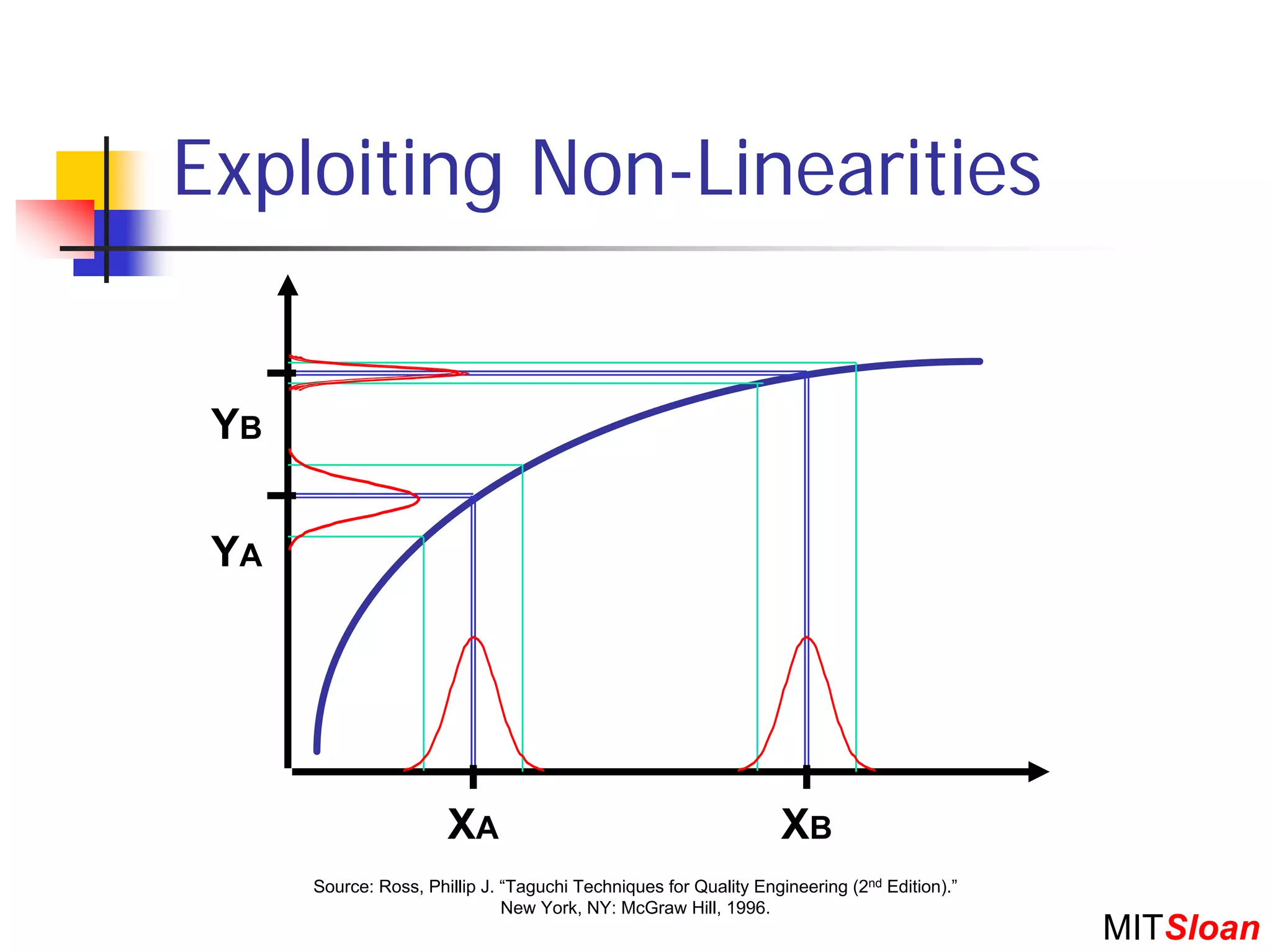
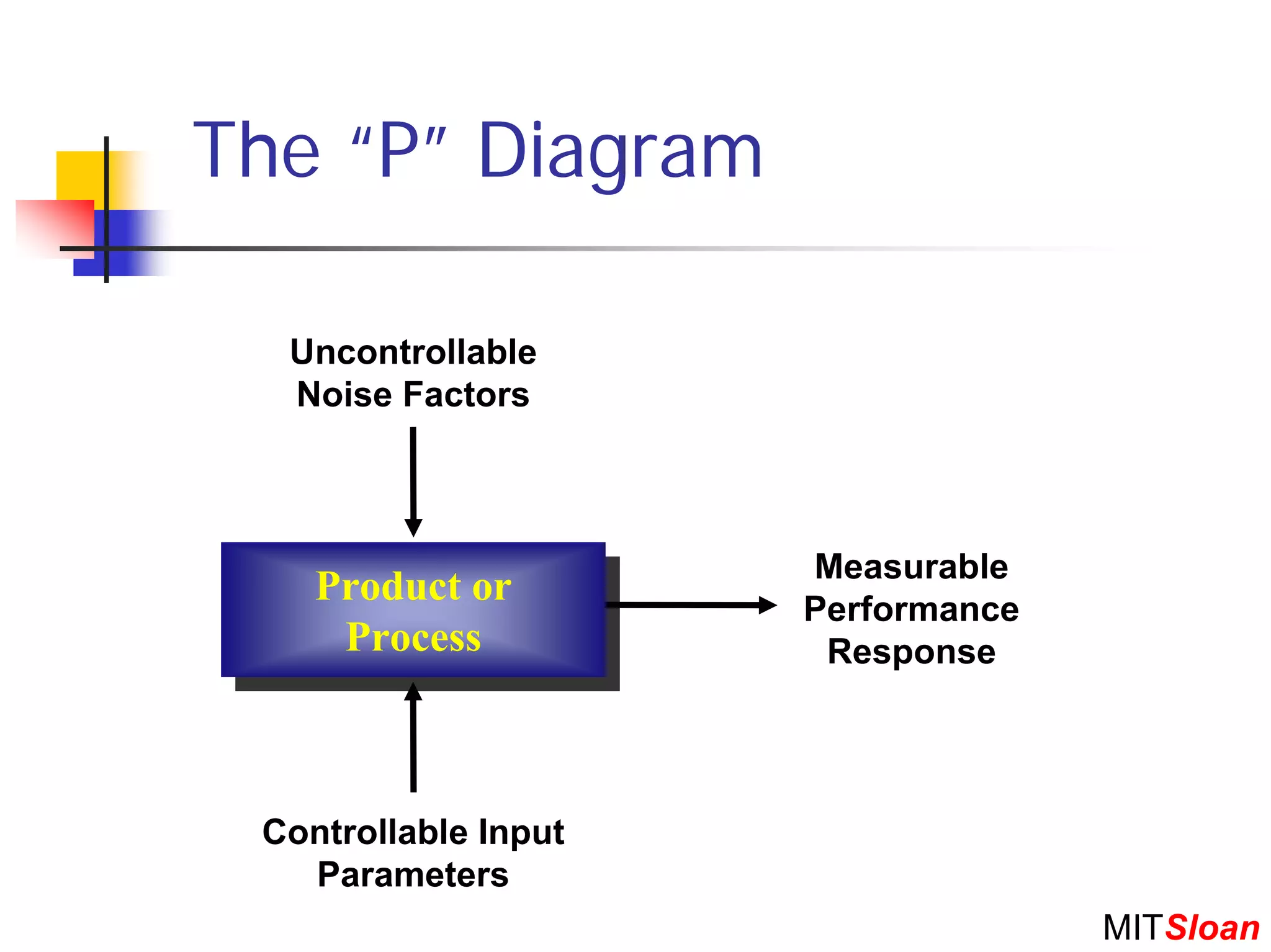
The document discusses Taguchi techniques for robust design and quality engineering. It describes the parameter design procedure which involves: (1) defining controllable parameters, uncontrollable noise factors, and measurable responses; (2) selecting an objective function to optimize; (3) planning experiments such as full factorial, fractional factorial, or orthogonal arrays; (4) running the experiment; (5) analyzing results to identify optimal parameter settings; and (6) selecting setpoints and conducting additional experiments if needed. The goal is to design products and processes that perform well even in the presence of uncontrollable noise factors.

![General Loss Function
Product & Process Engineer (a priori)
Manufacturing (daily)
[
k ⋅ σ + (µ − m )
2 2
]
Nominal Value
Average Value
Variance
Cost Factor
MITSloan](https://image.slidesharecdn.com/lec15robustdesign-121208182820-phpapp01/75/Robust-Design-4-2048.jpg)







![Types of Objective Functions
Larger-the-Better Smaller-the-Better
e.g. performance e.g. variance
ƒ(y) = y2 ƒ(y) = 1/y2
Nominal-the-Best Signal-to-Noise
e.g. target e.g. trade-off
ƒ(y) = 1/(y–t)2 ƒ(y) = 10log[µ2/σ2]
MITSloan](https://image.slidesharecdn.com/lec15robustdesign-121208182820-phpapp01/75/Robust-Design-14-2048.jpg)