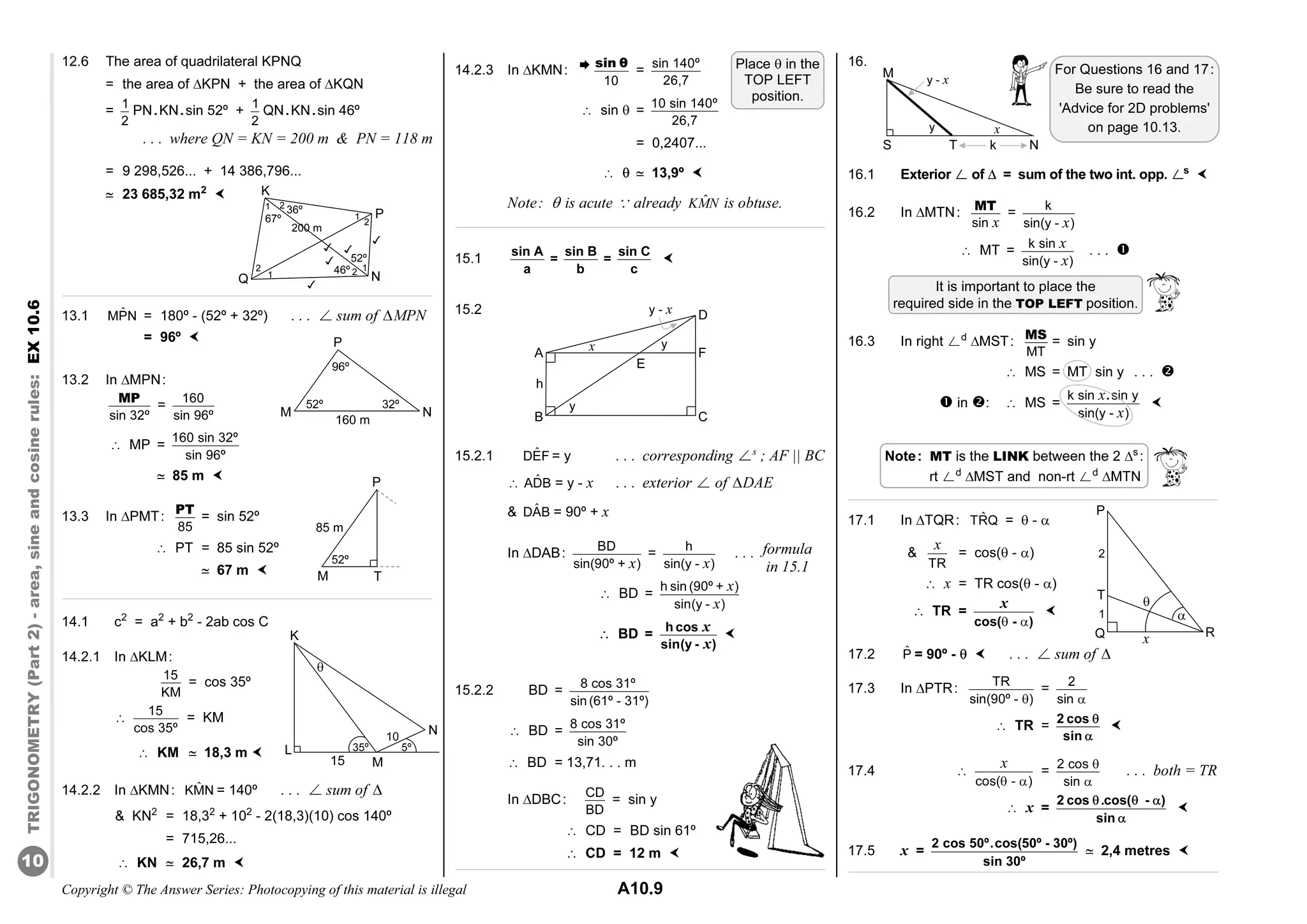
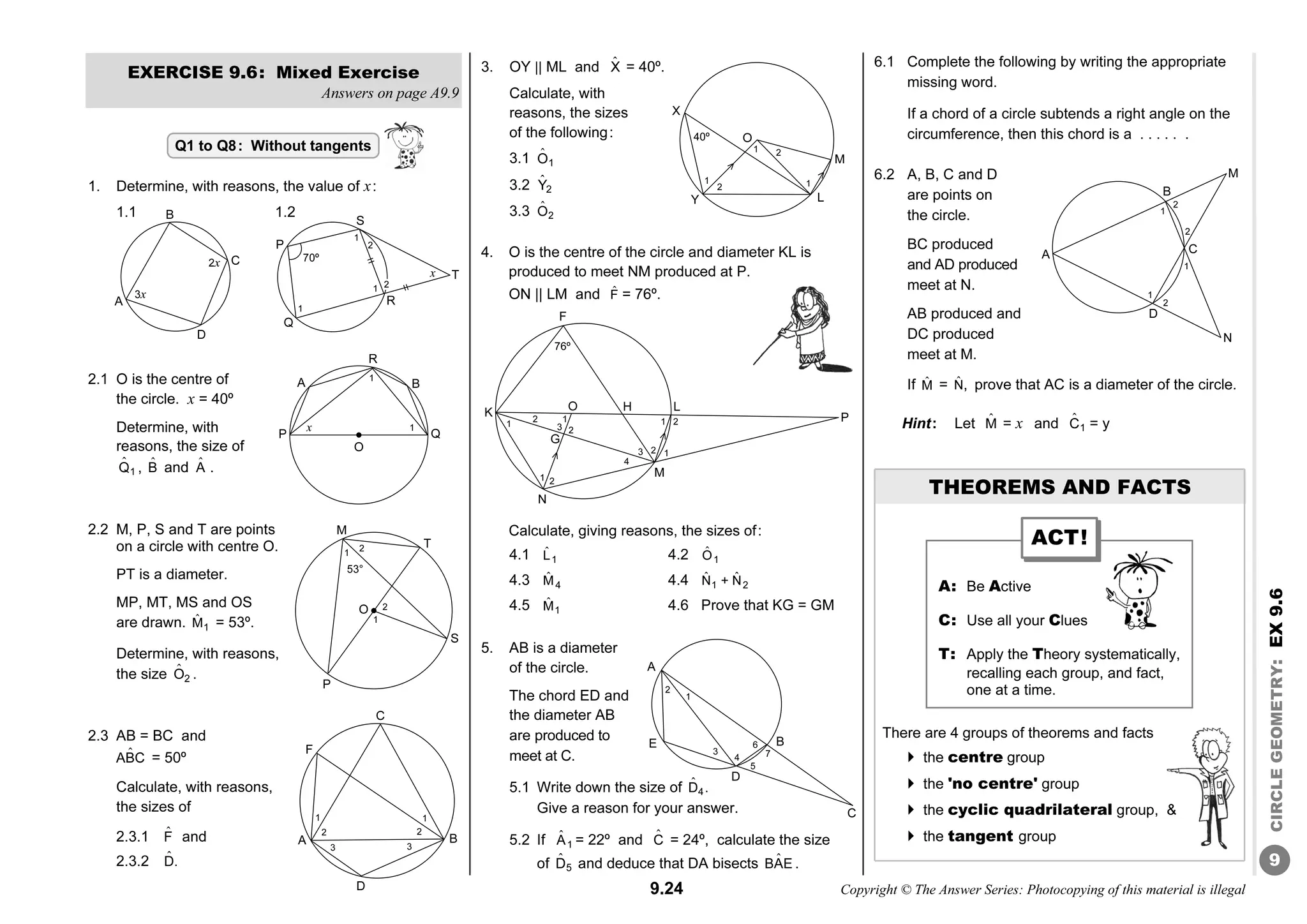
The document is a comprehensive study guide for Grade 11 Mathematics based on the CAPS curriculum. It includes detailed explanations, exercises, and solutions for various mathematical topics, preparing learners effectively for their exams. Key features also entail practice exam papers and guidelines for exam preparation, aimed at fostering a solid foundation in mathematics for higher grades.








![6.33 Copyright © The Answer Series: Photocopying of this material is illegal
6
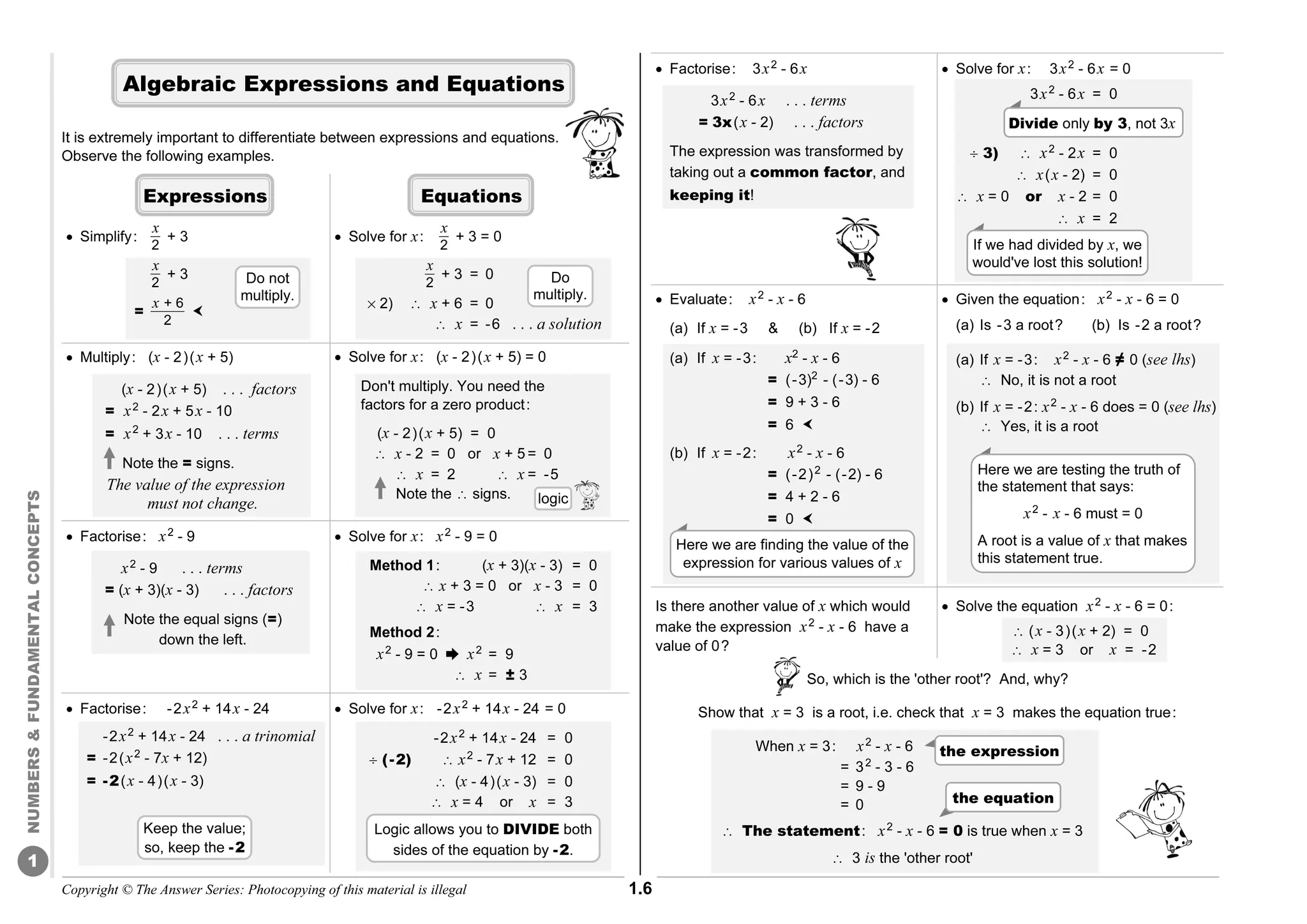
FUNCTIONS
GRAPHS
Note: The coordinates of the turning points
The coordinates of the axis-intercepts.
TRIGONOMETRIC GRAPHS
Point-by-point Plotting
Essential for point-by-point plotting of the basic graphs for ∈[0º; 360º]:
Know the critical values of the ratios
Know the signs of the ratios in the 4 quadrants
'The wheels' combine the critical values and the signs of the ratios.
Use the wheels to plot the 'critical points' before drawing the waves.
Decide where to start: Start at the beginning of the wave.
Choose the scale for each graph: All the critical values are on the wheels.
Extend the domain to: ∈[-360º; 360º]
Use the wheels to write down the critical values of negative angles
by going clockwise:
Plot points for all 3 basic graphs
y = sin θ:
y = cos θ:
y = tan θ:
x
y
O
Without
the use
of a
calculator.
Consider each wave
as being divided
into 4 quarters
Features of the graphs:
For both y = sin y = cos :
The amplitude = 1 unit
The range: -1 ≤ y ≤ 1
The maximum value = 1
The minimum value = -1
The period = 360º
y = tan θ:
The range: y∈R The period = 180º
The asymptotes: x = -270º ; x = -90º ; x = 90º ; x = 270º
y = sin θ:
y
O
1
-1
(0º; 0) (360º;0)
(180º;0)
(90º; 1)
(270º; -1)
y = cos θ:
y
O
(0º;1)
-1
(90º;0) (270º;0)
(360º; 1)
(180º; -1)
y
360º
(180º; 0)
1
-1
(45º; 1) (225º; 1)
(0º;0)
(135º; -1) (315º; -1)
O
x = 90º x = 270º
I II III IV I II III IV
y
(-90º; -1)
(-360º;0) (-180º;0)
1
-1
(0º; 0) (360º;0)
(180º;0)
(90º; 1)
(270º; -1)
(-270º; 1)
O
(-360º;1)
-1
(-270º;0) (-90º;0)
(-180º; -1)
y
O
(0º;1)
(90º;0) (270º;0)
(360º; 1)
(180º; -1)
I II III IV I II III IV
(-180º;0)
(-315º; 1) (-135º; 1)
(-225º; -1) (-45º; -1)
y
(360º; 0)
(180º; 0)
1
-1
(45º; 1) (225º; 1)
(135º; -1) (315º; -1)
O
(-360º;0)
x = -270º x = -90º x = 90º x = 270º
I II III IV I II III IV
e.g.
cos(-180º) = -1
sin(-270º) = 1 tan(-135º) = 1
O
0 0
-1
-
- 270º
1
O
-1 1
0
-
-180º
0
0 0
-1
O
-
-135º
-1
1
1
cos θ:
-1 1
0
0
0 0
1
--1
sin θ: tan θ:
0 0
-1 1
-1
1
+
-
-
+-
-
6b](https://image.slidesharecdn.com/gr-11-maths-3-in-1-extracts-240602024305-af05bbad/75/Gr-11-Maths-3-in-1-extract-pdf-study-com-11-2048.jpg)
![7.15 Copyright © The Answer Series: Photocopying of this material is illegal
7
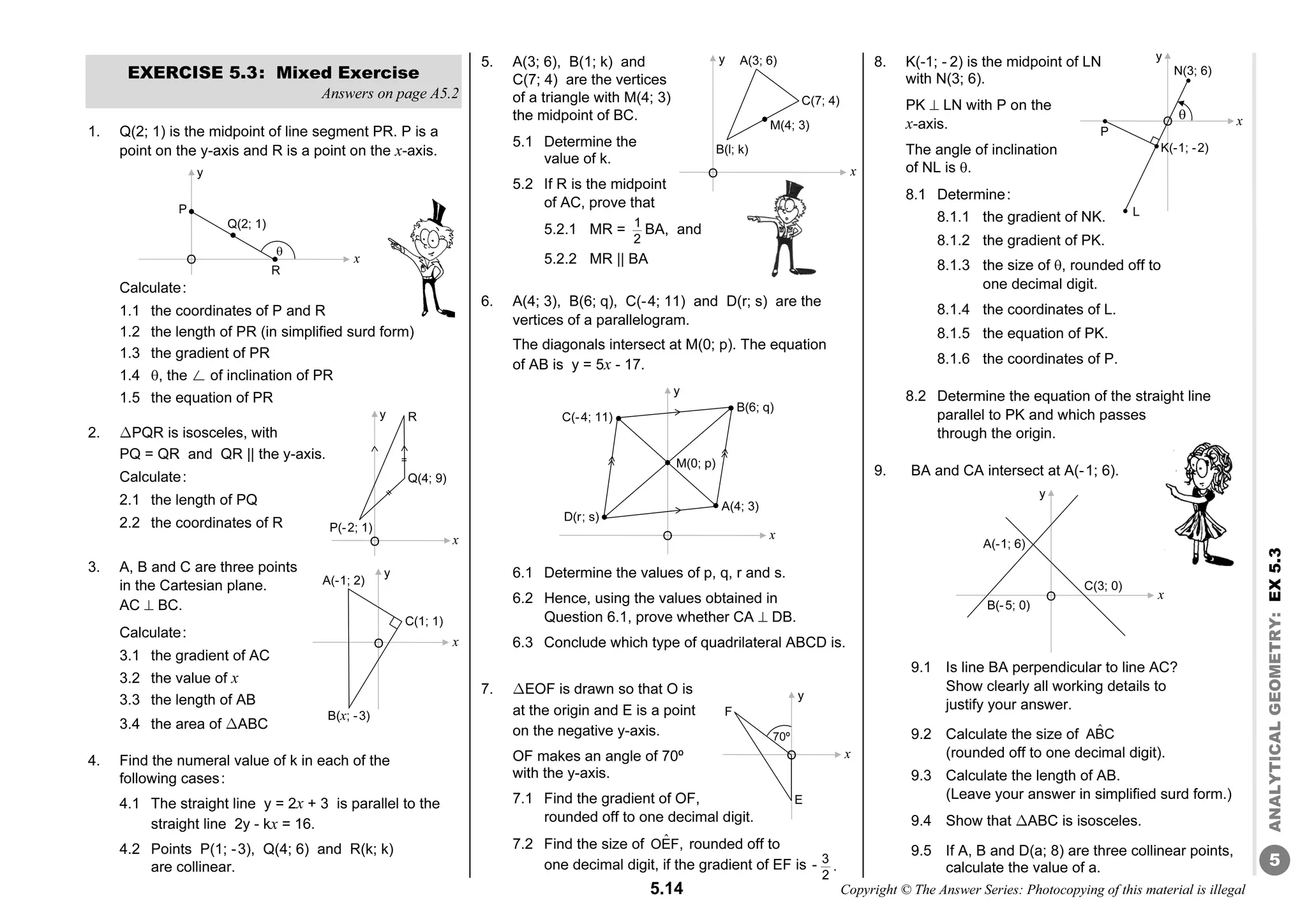
TRIGONOMETRY
(Part
1)
-
General
These 3 angles are co-terminal, i.e. they have the same terminal arm, OY.
The sine of all 3 angles is 1, their cosine is 0 and their tan is undefined.
30º -330º 150º -210º 210º -150º 330º -30º
Trigonometry Unlimited: All Angles!
Considering all possible angles, including negative angles
In considering the domain [0º; 360º], we have considered all 4 quadrants, but only
angles rotating anticlockwise, and only 1 revolution.
Rotating anticlockwise or clockwise, through any number of revolutions covers
the same 4 quadrants with the same results!
General forms: (θ ± 360º) ; (-θ)
Rotating through revolutions, anticlockwise and clockwise
e.g. (1) Compare: 30º ; 390º and -330º
These are 3 different ø
s
, but they are 'co-terminal', i.e. their end arms coincide.
â They have the same trig ratios:
sin 30º = sin 390º = sin(-330º) = 1
2
(2) Compare: 330º ; 690º ; -30º ; -390º
Standard positions:
These angles are co-terminal.
â They have the same trig ratios.
sin 330º = sin 690º = sin(-30º) = sin(-390º) = - 1
2
(3) Compare: 90º ; 450º ; -270º
450º = 90º + 360º
-270º = 90º -
- 360º
We conclude the following reduction formulae for θ ± 360º:
Rotating clockwise
If θ is then -θ is
Compare 30º ; 150º ; 210º ; 330º
to: -30º ; -150º ; -210º ; -330º
The following pairs of angles are co-terminal.
â They have the same trigonometric ratios.
I: sin(-330º) II: sin(-210º) III: sin(-150º) IV: sin(-30º)
= sin 30º = sin 150º = sin 210º = sin 330º
= 1
2
= 1
2
= - 1
2
= - 1
2
30º
x
y
O
P
390º = 30º + 360º
x
y
O
P
-330º = 30º - 360º
x
y
O
P
x
y
O
θ anticlockwise
rotation
x
y
O
-θ
clockwise
rotation
x
y
O
30º
-30º
x
y
O
150º
-150º
30º
30º
x
y
O
150º
-210º
P
II
x
y
O
210º
-150º
III
P
x
y
O
330º
IV
-30º
P
-330º
x
y
O
P
I
30º
x
y
O
330º
-330º
30º
30º
y
O
210º
-210º
30º
30º
x
x
y
O
450º
-270º
So: sin (-330º) = + sin 30º sin (-150º) = - sin 30º
sin (-210º) = + sin 30º sin (-30º) = - sin 30º
sin( + 360º) = sin cos( + 360º) = cos tan( + 360º) = tan
sin( - 360º) = sin cos( - 360º) = cos tan( - 360º) = tan
-30º ;
-390º
y
O x
330º ;
690º
y
O x
The reduction formulae for -θ:
sin(-) = -
-sin tan(-) = -
-tan
Compare to:
sin(360º - ) = -
-sin tan(360º - ) = -
-tan
cos(360º - ) = +cos
cos(-) = +cos
Consider acute](https://image.slidesharecdn.com/gr-11-maths-3-in-1-extracts-240602024305-af05bbad/75/Gr-11-Maths-3-in-1-extract-pdf-study-com-12-2048.jpg)



![Copyright © The Answer Series: Photocopying of this material is illegal Q6
EXAM
PAPERS:
PAPER
2
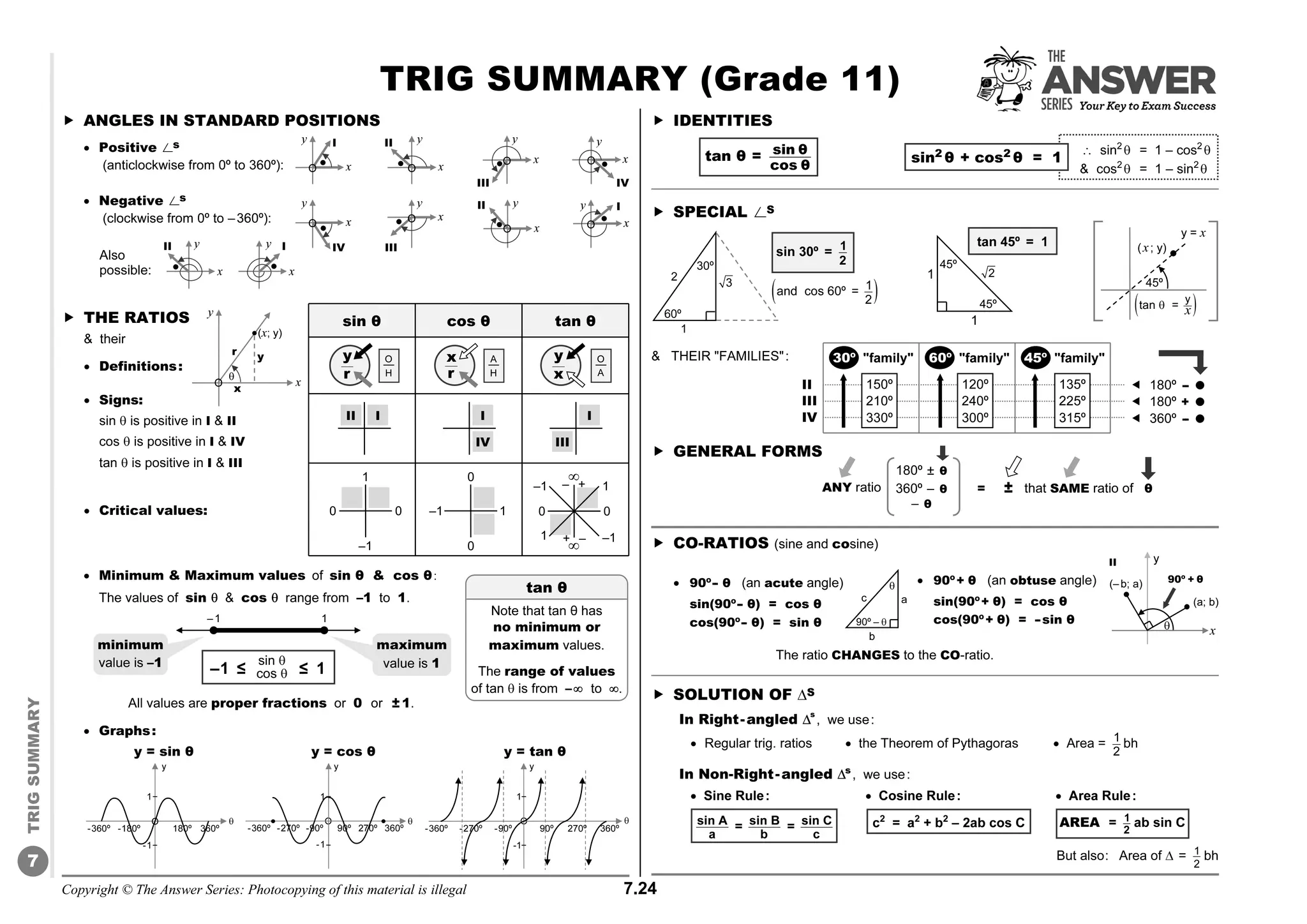
MEASUREMENT [6]
QUESTION 8
A solid metallic hemisphere has a
radius of 3 cm. It is made of metal A.
To reduce its weight a conical hole is
drilled into the hemisphere (as shown in
the diagram) and it is completely filled with a lighter
metal B. The conical hole has a radius of 1,5 cm and a
depth of
8
9
cm.
Calculate the ratio of the volume of metal A to the
volume of metal B. [6]
EUCLIDEAN GEOMETRY [40]
QUESTION 9
9.1 Complete the statement so that it is valid:
The line drawn from the centre of the circle
perpendicular to the chord . . . (1)
9.2 In the diagram, O is the
centre of the circle.
The diameter DE is
perpendicular to the
chord PQ at C.
DE = 20 cm and CE = 2 cm.
Calculate the length of the following with reasons:
9.2.1 OC 9.2.2 PQ (2)(4) [7]
QUESTION 10
10.1 In the diagram, O is the
centre of the circle and
A, B and D are points on
the circle.
Use Euclidean geometry methods to prove the
theorem which states that ˆ
AOB = ˆ
2ADB. (5)
10.2 In the diagram, M is the centre of the circle.
A, B, C, K and T lie on the circle.
AT produced and CK produced meet in N.
Also NA = NC and B̂ = 38º.
10.2.1 Calculate, with reasons, the size of the
following angles:
(a) ˆ
KMA (b) ˆ
2
T (2)(2)
(c) Ĉ (d) ˆ
4
K (2)(2)
10.2.2 Show that NK = NT. (2)
10.2.3 Prove that AMKN is a cyclic
quadrilateral. (3) [18]
QUESTION 11
11.1 Complete the following statement so that it
is valid:
The angle between a chord and a tangent
at the point of contact is . . . (1)
11.2 In the diagram, EA is a tangent to circle ABCD
at A.
AC is a tangent to circle CDFG at C.
CE and AG intersect at D.
If ˆ
1
A = x and ˆ
1
E = y, prove the following with
reasons:
11.2.1 BCG || AE (5)
11.2.2 AE is a tangent to circle FED (5)
11.2.3 AB = AC (4) [15]
TOTAL: 150
B
1
A
C
D
E
F
G
1
1
1
1
1
2
2
2
2
2
2
3 3
3
4
x
5
y
P
E
C
O
D
Q
D
O
A
B
N
T
38º
1
1 2
2
3
4
B
C M
A
K](https://image.slidesharecdn.com/gr-11-maths-3-in-1-extracts-240602024305-af05bbad/75/Gr-11-Maths-3-in-1-extract-pdf-study-com-18-2048.jpg)
![M9 Copyright © The Answer Series: Photocopying of this material is illegal
EXAM
MEMOS:
PAPER
2
MEASUREMENT [6]
8. Volume of metal B (the cone)
=
1
3
r2
.h
=
1
3
(1,5)2
.
8
9
=
2
3
Volume of the hemisphere = 1
2
3
4
r
3
=
2
3
. 33
= 18
â Volume of metal A = 18 - 2
3
= 17
1
3
â The ratio:
Volume of metal A : Volume of metal B
= 17 1
3
:
2
3
% 3) = 52 : 2
2) = 26 : 1
EUCLIDEAN GEOMETRY [40]
9.1 . . . bisects the chord
9.2.1 OE = OD = 1
2
(20) = 10 cm
â OC = 8 cm . . . CE = 2 cm
9.2.2 In OPC:
PC2
= OP2
- OC2
. . . Pythagoras
= 102
- 82
= 36
â PC = 6 cm
â PQ = 12 cm . . . line from centre to chord
10.1 Construction: Join DO and
produce it to C
Proof:
Let ˆ
1
D = x
then  = x . . .
â ˆ
1
O = 2x
. . . ext. ø of DAO
Similarly, ˆ
2
O = 2y
â ˆ
AOB = 2x + 2y
= 2(x + y)
= 2 ˆ
ADB
10.2
10.2.1 (a) ˆ
KMA = 2(38º) . . .
= 76º
(b) ˆ
2
T = 38º . . . ext. ø of cyclic quad. BKTA
(c) Ĉ = 38º . . .
(d) ˆ
NAC = 38º . . . øs
opposite = sides
â ˆ
4
K = 38º . . . ext. ø of c.q. CKTA
10.2.2 In NKT: ˆ
4
K = ˆ
2
T . . . both = 38º in 10.2.1
â NK = NT . . . sides opp = øs
10.2.3 ˆ
KMA = 2(38º) . . . see 10.2.1(a)
N̂ = 180º - 2(38º) . . . sum of øs
of NKT
(see 10.2.2)
â ˆ
KMA + N̂ = 180º
â AMKN is a cyclic quadrilateral
. . . opposite øs
of quad upplementary
or conv. opp øs
of cyclic quad
11.1 . . . equal to the angle subtended by the chord
in the alternate segment.
11.2
11.2.1 ˆ
1
A = x . . . given
â ˆ
2
C = x . . . tan chord theorem
â ˆ
2
G = x . . . tan chord theorem
â ˆ
1
A = ˆ
2
G
â BCG || AE . . . alternate øs
=
11.2.2 ˆ
1
E = ˆ
3
C = y . . . alternate øs
; BG || AE
â ˆ
1
F = y . . . exterior ø of cyclic quad
â ˆ
1
E = ˆ
1
F
â AE is a tangent to ?FED
. . . converse tan-chord theorem
11.2.3 ˆ
1
C = ˆ
CAE . . . alternate øs
; BCG || AE
= B̂ . . . tan chord theorem
â ˆ
1
C = B̂
â AB = AC . . . sides opposite = øs
radii
= 1
2
diameter
ø at centre =
2 % ø at circumference
øs
in same segment
or, ext. ø of c.q. CKTA
r = 3 cm
r = 1 1
2
cm
h = 8
9
cm
P
E
C
O
D
Q
D
1
A
B
1 2
2
y
y
x
x
C
O
øs
opp
= radii
B
1 A
C
D
E
F
G
1
1
1
1
1
2
2
2
2
2
2
3 3
3
4
x
5
y
N
T
38º
1
1 2
2
3
4
B
C M
A
K](https://image.slidesharecdn.com/gr-11-maths-3-in-1-extracts-240602024305-af05bbad/75/Gr-11-Maths-3-in-1-extract-pdf-study-com-19-2048.jpg)




![Copyright © The Answer Series: Photocopying of this material is illegal A6.1
FUNCTIONS
GRAPHS:
EX
6.1
6
EXERCISE 6.1: Parabolas
Questions on page 6.13
1.1 (a) (-3; -5) (b) y = x2
+ 6x + 4 (c) (0; 4)
1.2 (a) (1; 4) (b) y = -x2
+ 2x + 3 (c) (0; 3)
1.3 (a) (-2; 1) (b) y = 2x2
+ 8x + 9 (c) (0; 9)
2.1 (a) y = x2
+ 8x + 10 . . . std form
y = x2
+ 8x + 42
+ 10 -- 16
y = (x + 4)2
- 6 . . . t.pt. form
(b) 4 units left and 6 units down
(c) turning point: (- 4; -6)
(d) y-int: (0; 10) . . .
2.2 (a) y = x2
- 6x + 11
y = x2
- 6x + 32
+ 11 -- 9
y = (x - 3)2
+ 2
(b) 3 units right and 2 units up
(c) turning point: (3; 2)
(d) y-intercept: (0; 11) . . . see the standard form
2.3 (a) y = -x2
+ 4x + 5
y = -(x2
- 4x - 5)
y = -(x2
- 4x + 22
- 5 - 4)
y = -[(x - 2)2
- 9]
y = -(x - 2)2
+ 9
(b) 2 units right and 9 units up
(c) turning point: (2; 9)
(d) y-intercept: (0; 5) . . . see the standard form
3.1 (a) y = x2
- 7x + 12 3.2 (a) y = -(x2
- 7x + 12)
y = (x - 3)(x - 4) y = -(x - 3)(x - 4)
(b) x = 3 and x = 4 (b) x = 3 x = 4
(c) x = 3 1
2
(c) x = 3 1
2
3.3 (a) y = (x - 1)2
- 4 (b) x = -1 and x = 3
y = x2
- 2x - 3 (c) x =
-1 + 3
2
= 1
y = (x + 1)(x - 3)
4. (a) y = (x - 3)2
- 1
(b) y = (x + 2)2
+ 5
5.1 (a) (b)
(c) (d)
(e) (f)
(g) (h)
(i) (j)
5.2.1 (a) 3 units down
(b) 3 units left
(d) 5 units right and 2 units down
(f) 2 units left and 4 units up
5.2.2 (c) 4 units down
(e) 2 units right and 1 unit up
6.1
(a) y = ax2
+ 3 (b) y = ax2
+ 4
(3; 6): 6 = a(3)2
+ 3 (-4; 0): 0 = a(-4)2
+ 4
3 = 9a -4 = 16a
a =
1
3
a = -
1
4
Eqn: y =
1
3
x2
+ 3 Eqn: y = -
1
4
x2
+ 4
(c) y = ax2
. . . c = 0
(-3; 4): 4 = a(-3)2
4 = 9a
a =
4
9
Eqn: y =
4
9
x2
(d) t.p.: (2; 0) (e) t.p.: (1; 2)
y = a(x - 2)2
y = a(x - 1)2
+ 2
(0; 2): 2 = a(-2)2
(0; 5): 5 = a(-1)2
+ 2
a =
1
2
a = 3
Eqn: y =
1
2
(x - 2)2
Eqn: y = 3(x - 1)2
+ 2
(f) Symmetry x = 2 Maximum y = 9
y = a(x - 2)2
+ 9
(-1; 0): 0 = a(-1 - 2)2
+ 9
9a = -9
a = -1
Eqn: y = -(x - 2)2
+ 9
The y-intercept
Either
read it from the
standard form
or
substitute x = 0
in the t.p. form
see the
std form
y
x
O
(0; 3)
y
x
O
(-2; -1)
-5
y
x
O
(-5; 2)
27
y
x
O
(0; -5)
(-1; -2)
(a) ¡ (c): Use y = ax2 + q
These graphs are symmetrical about the y-axis.
(d) ¡ (f): Use y = a(x - p)2 + q
These graphs are not symmetrical about the y-axis.
x-ints:
(x - 2)2
= 4
x - 2 = 2
x = 2 2
= 0 or 4
y
x
(4; 0)
(2; -4)
(0; 0)
O
x-ints:
-(2x - 1)2
+ 9 = 0
(2x - 1)2
= 9
2x - 1 = 3
2x = 1 3
x = 1 3
2
x = -1 or 2
y
x
(2; 0)
(0; 8)
O
(-1; 0)
1
2
; 9
x-ints:
3(x - 1)2
- 12 = 0
3(x - 1)2
= 12
(x - 1)2
= 4
x - 1 = 2
x = 1 2
x = -1 or 3
x-int: x = 3 ... the 'zero
value' of x
for ( )2
= 0
y
x
O
(0; 9)
3
x-ints:
-x2
+ 4 = 0
x2
= 4
x = 2
y
x
O
(-2; 0) (2; 0)
(0; 4)
y
x
O
(0; 9)
3
2
- ; 0
x-int: x = - 3
2
... the
'zero value'
of x for
( )2
= 0
Note:
a = 1, given
y
x
(1; -12)
(0; -9)
O
(-1; 0) (3; 0)](https://image.slidesharecdn.com/gr-11-maths-3-in-1-extracts-240602024305-af05bbad/75/Gr-11-Maths-3-in-1-extract-pdf-study-com-25-2048.jpg)