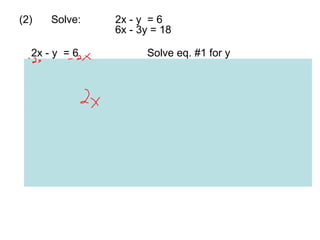
The document discusses solving systems of linear equations using substitution and elimination methods. It provides 4 examples of solving systems of 2 equations with 2 unknowns. The substitution method involves solving one equation for one variable in terms of the other and substituting it into the second equation. The elimination method involves multiplying equations by constants and adding/subtracting them to eliminate one variable. Both methods are shown to yield the solution point that satisfies both equations.

1. Solving Linear Systems by the Substitution Method: A system of linear eqs. consists of more than one linear eq. with the same variables, mostly x & y. The solution of a system of linear eqs. includes all the ordered pairs that make all of the eqs. in the system true at the same time. On a graph, this would be the point at which all lines intersect.

2. Solving Linear Systems by the Substitution (1) Solve: 3x + y = 20 2x + 3y = 18 3x + y = 20 Solve eq. #1 for y y = -3x + 20 eq. #1 solved for y. 2x + 3y = 18 Substitute -3x + 20 for y into eq.#2 2x + 3(-3x + 20) = 18 2x - 9x + 60 = 18 Now solve for x. -7x = -42 Like terms combined x = 6

3. Solving Linear Systems by the Substitution x = 6 3x + y = 20 Now substitute 6 for x into eq. #1 3(6) + y = 20 and solve for y 18 + y = 20 y = 2

4. Check Answer So (x,y) = (6,2). Let’s check this just to be sure that we have the right solution to the system. Substitute 6 for x and 2 for y in both equations of the system. Check eq. #1 3x + y = 20 3(6) + 2 = 20 Check eq. #2 2x + 3y = 18 2(6) + 3(2) = 18 Because (x,y) = (6,2) satisfies both eqs., it is therefore the solution of the system.

5. (2) Solve: 2x - y = 6 6x - 3y = 18 2x - y = 6 Solve eq. #1 for y y = 2x – 6 eq. #1 solved for y. 6x - 3y = 18 Substitute 2x - 6 for y into eq. #2 6x - 3(2x - 6) = 18 Now solve for x. 6x - 6x + 18 = 18 0 = 0 True. Like terms combined. But we have no value for x. Also, the left side of the eq. equals to the right side. This suggests that both the eqs. share the same line and that there are infinite number of (x,y) solutions that satisfies this system. This can be verified by solving both eqs. for y (in the form of y = mx + b).

6. (3) Solve: 3x = y + 5 6x + 10 = 2y 3x = y + 5 Solve eq. #1 for y y = 3x – 5 eq. #1 solved for y. 6x + 10 = 2y Substitute 3x - 5 for y into eq. #2 6x + 10 = 2(3x - 5) Now solve for x. 6x + 10 = 6x – 10 Combine like terms 0 = -20 False. Like terms combined. But we have no value for x. Also, the left side of the eq. does not equal to the right side. This suggests that the eqs. do not share a common (x,y) point. They are parallel lines. So there is no solution for this system. This can be verified by solving both eqs. for y (in the form of y = mx + b).

7. (4) Solve: 3x + 2y = 6 -6x + 4y = -8 3x + 2y = 6 Solve eq. #1 for y y = -3/2x + 3 eq. #1 solved for y. -6x + 4y = -8 Substitute -3/2x + 3 for y into eq. #2 -6x + 4(-3/2x + 3) = -8 Now solve for x. -6x -6x + 12 = -8-12x = -20 Like terms combined x = 5/3 3x + 2y = 6 Now substitute 5/3 for x into eq. #1 and solve for y 3(5/3) + 2y = 6 5 + 2y = 6 2y = 1y = ½ So (x,y) = (5/3, 1/2).

8. Let’s check this just to be sure that we have the right solution to the system. 3x + 2y = 6 Check eq. #1 3(5/3) + 2(1/2)= 6 Substitute 5/3 for x and 1/2 for y in both eqs. of the system. 5 + 1 = 6 6 = 6 Check eq. #2 -6x + 4y = -8 -6(5/3) + 4(1/2) = -8 Substitute 5/3 for x and 1/2 for y in both eqs. of the system. -10 + 2 = -8 -8 = -8 Because (x,y) = (5/3,1/2) satisfies both eqs., it is therefore the solution of the system.

9. Bob and Mary went to the movies. Bob purchased 3 medium bags of popcorns and 2 large drinks and paid $11.00. Mary purchased 2 medium bags of popcorns and 4 large drinks and ended up paying $12.00. What was the price of a medium bag of popcorn and what was the price of a large drink? Denote p the price of a medium bag of popcorn and d the price of a large drink. Then we have 3 p + 2 d = 11 2 p + 4 d = 12

10. 3 p + 2 d = 11 2 p + 4 d = 12 -6 p - 4 d = -22 2 p + 4 d = 12 -4 p = -10 p = 2.50 Substituting back and solving for d we get d = 1.75. (multiply the first by -2) (add the first to the second) Medium bag of popcorn costs $2.50 and a large drink costs $1.75.

11. Solving Linear Systems by Elimination (1) Solve: 3x + y = 20 2x + 3 y = 18 -3(3x + y ) =-3*20 multiply eq#1 by -3 -9x – 3 y = -60 add eq#1 + eq#2 2x + 3 y = 18 to eliminate y -7x + 0 y = -42 x=6

12. Solving Linear Systems by Elimination (1) Solve: 3x + y = 20 2x + 3 y = 18 Given x= 6 solve for y 3x + y = 20 3(6) + y = 20 y = 20 – 18 = 2 2x + 3 y = 18 2(6) + 3 y = 18 3 y =18 – 12 = 6/3 = 2  (6, 2)

13. Solving Linear Systems by Elimination (4) Solve: 3x + 2y = 6 -6x + 4y = -8 3x + 2y = 6 -2(3x +2y) = -2*6 multiply by -2 -6x – 4y =-12 -6x + 4y = -8 -12x = -20 x = -20/-12 = 5/3

14. Solving Linear Systems by Elimination (4) Solve: 3x + 2y = 6 -6x + 4y = -8 Given: x = 5/3 solve for y 3x + 2y = 6 3(5/3) + 2y = 6 2y = 6 – 3(5/3) = 1 y=1/2 -6x + 4y = -8 -6(5/3) + 4y = -8 4y = -8 + 6(5/3) = 2 y=1/2  (5/3, ½)

15. Postulate 13 Parallel Postulate If there is a line and a point not on the line, then there is exactly one line through the point parallel to the given line

16. Postulate 14 Perpendicular Postulate If there is a line and a point not on the line, then there is exactly one line through the point perpendicular to the given line