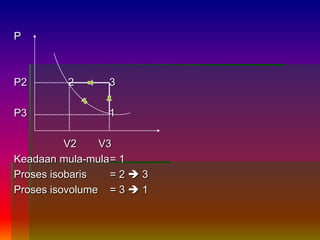
Tiga kalimat ringkasan dokumen tersebut adalah: 1. Dokumen tersebut menjelaskan berbagai jenis kerja dalam termodinamika seperti kerja mekanik, ekspansi, gravitasi, permukaan, dan listrik. 2. Metode penghitungan kerja total dengan mengintegrasikan persamaan kerja dan contoh soal penerapannya. 3. Dibahas pula proses-proses dalam termodinamika seperti isovoume, isobaris, isot

1. TERMODINAMIKA

2. KERJA
Dalam termodinamika kerja umu
didefinisikan sebagai gaya kali jarak
(W = F.s). Terdapat berbagai jenis kerja
yang didefinisikan dengan persamaan-
persamaan :
Kerja mekanik DW = F. ds
Kerja ekspansi DW = p. dV
Kerja gravitasi DW = mgdh
Kerja permukaan DW = γ d A
Kerja listrik DW = € d q

3. Dimana:
F = gaya,
P = tekanan
m = massa
g = gaya gravitasi
γ = tegangan permukaan
€ = perbedaan potensial
V = volume sistem
h = ketinggian
A = luas permukaan
q = muatan listrik misal, arus x waktu =
I.dT

4. • Tanda yang akan digunakan
adalah :
- positif (+) bila sistem melakukan
kerja terhadap sekelilingnya
- negatif (-) bila sekelilingnya
melakukan kerja terhadap sistem
• Kerja total yang dilakukan sistem
dapat diperoleh dengan
mengintegrasikan persamaan di
atas , misalnya : kerja eskpansi
W = ∫ p dV

6. Latihan:
• Berapa kerja yang dilakukan terhadap sistem jika gas
dikompresi melawan tekanan konstan 5 atm dan gas
dikompresi dari 5 dm3 menjadi 1 dm3 pada 300 K.
nyatakan W dalam kJ,
W = ∫ p dV
V2
W = ∫ p dV = p (V2 – V1 )
V1
Karena p konstan, maka :
W = 5 atm x (1-5) dm3 = - 20 atm . dm3
1 atm = 1,0132 .102 kN.m-2
= -20 atm . dm3 x 1,0132 .102 kN.m-2. atm-1 .
dm-3

7. Latihan:
• Satu mol gas ideal pada 3 atm dan 300 K diekspansi secara
isoterm menjadi dua kali volume semula melawan tekanan
eksternal 1,5 atm, maka hitunglah kerjanya atau W:
V1 = RT/p = (0,082 dm3 atm K-1 mol-1) (300 K) (1 mol)
3 atm
= 8,2 dm3
V2 = p1V1/p2 = (3 atm) (8,2 dm3) = 16,4 dm3
1,5 atm
W = peks dV = (1,5 atm) (16,4 – 8,2) dm3
= 12,3 atm dm3 = 12,3 J
Karena kerja dilakukan oleh sistem maka nilainya positif

8. Latihan:
 Satu mol gas ideal pada 3 atm dan 300 K diekspansi
secara isoterm dan reversibel menjadi dua kali
volume semula, maka hitunglah kerjanya atau W:
 Karena ekspansi reversibel maka harga W adalah :
W = n RT ln V2/V1
= ( 1 mol ) ( 8,314 J K-1 mol-1) (300 K) ln 2 V1
V1
= = 1,72 x 103 J
Dibanding dengan soal diatas kerja ekspansi lebih
besar . Kerja yang dilakukan dalam ekspansi
reversiberl adalah maksimum

9. Latihan:
 Berapa kerja yang dilakukan terhadap sistem jika satu mol gas
ideal pada 300 k dikompres secara isotermal dan reversibel
menjadi seperlima dari volume semula?
 Diket : N= 1mol, T=300 k, V2=1/5
 Jwb : w = nRT.in v2/v1
 = ( 1 mol ) ( 8,314 J K-1mol-1)(300K) [in 1/5 v1/v1]
 = 2494,2(-1,609)
 = -4013,1678

10.  KERJA YANG DILAKUKAN SISTEM
TERGANTUNG PADA PROSES YANG
BERSANGKUTAN, PROSES-PROSES
YANG TERJADI :
1. PROSES ISOVOLUME, PROSES PADA
VOLUME TETAP;
v2
W = ∫ P. dv = 0
v1
KARENA TIDAK ADA PERUBAHAN
VOLUME MAKA dV = 0 SEHINGGA
PERSAMAAN MENJADI :
dU = dQv atau dU = n Cv dT

11.  Cv ADALAH KAPASITAS MOLAR PADA
VOLUME TETAP. KARENA ENERGI DALAM
SISTEM TIDAK TERGANTUNG PADA
PROSES demikian juga dT sehingga berlaku
untuk semua proses.
2. PROSES ISOBARIS PROSES PADA
TEKANAN TETAP ;
v2
W = ∫ P. dv = 0
v1
v2
W =P ∫ P. dv = P = (V2 – V1
v1
KAPASITAS PANAS MOLAR PADA
TEKANAN TETAP ADALAH Cp, MAKA;

12.  dQ = n Cp dT
 DAN KERJA PADA TEKANAN TETAP:
 dW = P dV = nR dT
MAKA ; dU = dQ – dW
nCv dT = n Cp dT – nR dT
ATAU ; Cp – Cv R
R= konstanta gas umum

13. 3. PROSES ISOTERMAL, PROSES PADA
TEMPERATUR TETAP;
W = n RT ln P1/P2
PADA PROSES ISOTERMAL dT = 0 SEHINGGA
;
dU = 0 dan dQ = dW
4. PROSES ADIABATIS, PROSES BERLANGSUNG
TANPA ADANYA ALIRAN PANAS YANG MASUK
ATAUPUN KELUAR, JADI;
dQ = 0
v2 v2
W = ∫ C. dv = C 1 V1 - γ
v1 Vγ γ – 1 v1

14.  W = 1 (P2V2 –P1V1)
γ – 1
5. PROSES REVERSIBERL, PROSES YANG
DAPAT KEMBALI KE KEADAAN SEMULA
TANPA ADANYA KALOR YANG BERPINDAH
DAN TANPA KERJA YANG DILAKUKAN,
ARTINYA TANPA ADANYA PERUBAHAN
APAPUN BAIK SISTEM ATAU
LINGKLUNGANNYA. PADA
KENYATAANNYA DI ALAM TIDAK ADA
PROSES INI YANG ADA PROSES
IRREVERSIBEL

15.  Gas ideal monoatomik mula-mula mempunyai
tekanan P1, temperatur T1 dan volume V1. Gas ini
kemudian ditekan secara isoterm sehingga
tekanannya menjadi P2 = 3P1. selanjutnya pada
tekanan tersebut gas dibiarkan mengembang
secara isobaris sehingga volumenya menjadi
V3=2V2, dan akhirnya gas ini ditekan sehingga
semua besaran kembali pada keadaan semula.
Gambarkan proses-prses tersebut dalam diagram
 P-V:

16. P
P2 2 3
P3 1
V2 V3
Keadaan mula-mula= 1
Proses isobaris = 2  3
Proses isovolume = 3  1

17.  1 cm3 air bila diuapkan pada tekanan 1 atm akan menjadi
uap dengan volume 1671 cm3 . Panas penguapan pada
tekanan ini adalah 539 kal/gram.hitunglah usaha luar dan
penambahan tenaga dalamnya.
 Jawab:
 Karena proses ini tekanannya konstan, maka usaha luarnya
adalah :
 W = p ( V2 – V1)
 = 1,013 . 1016 (1671 – 1)
 = 1,695 .109 erg
 = 169,5 Jaoule = 41 kal
 Massa 1 cm3 air adalah 1 gram. Jadi panas yang
diperlukan untuk menguapkan air adalah:
 Q= Ml=1 X 539 = 539 kali
 Dari hukum termodinamika :
 ∆ U = Q –W
 = 539 -41 = 498 kali

18. Hukum kedua termodinamika
 Tidak mungkin membuat mesin kalor yang
bekerja secara siklis yang dapat
mengubah kalor yang diserap seluruhnya
menjadi tenaga mekanik. Tidak mungkin
membuat mesin pendingin yang hanya
menyerap panas dari wadah yang
bertemperatur rendah dan mengalirkannya
ke wadah bertemperatur tinggi tanpa kerja
dari luar.