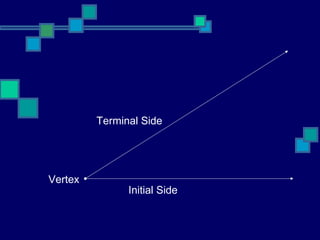
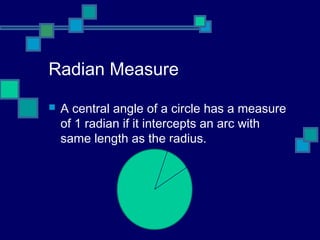
This document provides an overview of trigonometry and measuring angles. It defines common units of measurement for angles including degrees which are divided into minutes and seconds. It also introduces concepts like central angles, standard position, radian measure, and the relationship between circular arc length and the radius/radian measure of the central angle.

1. Trigonometry
The Measure of triangles.

2. Measuring Angles
 The most common unit to measure
angles is the degree (1o).
 The degree is subdivided into 60 equal
parts known as minutes (1’).
 The minute is subdivided into 60 equal
parts known as seconds (1”).

3. Measuring Angles
1 degree = 60 minutes
 1 minute = 60 seconds
 1 degree = 3600 seconds

4. Measuring Angles
Convert to degrees, Convert to degrees:
minutes and  35o 12’ 7”
seconds:
 35o + 12’ (1o /60’) + 7”
 329.125o
(1o/3600”)
 3290 + (.125 x 60)’
 about 35.202o
 329o + 7.5’
 329o + 7’ + (.5 x 60)”
 329o + 7’ + 30”
 329o 7’ 30”

5. Terminal Side
Vertex
Initial Side

6. Central Angle
 An angle with its vertex at the center of a
circle.

7. Standard Position
 An angle with its vertex at the origin.
 The initial side lies along the positive
x-axis.

8. Radian Measure
 A central angle of a circle has a measure
of 1 radian if it intercepts an arc with
same length as the radius.

9. Measuring Angles
Degrees Radians

10. Circular Arc Length
 s=rθ
 The central angle θ is always a radian
measure.
 If it is not you must convert it to a radian
measure.