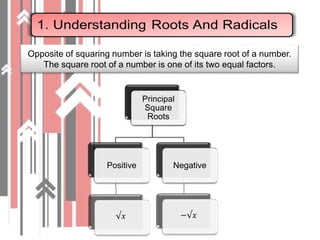
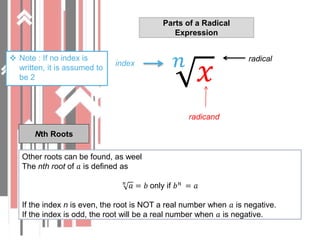
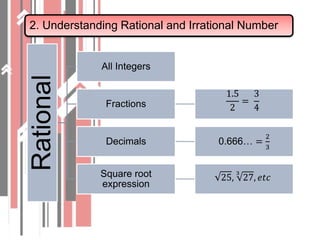
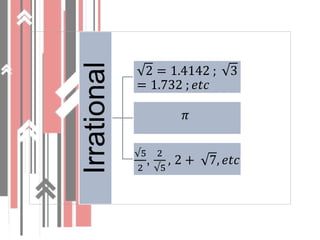
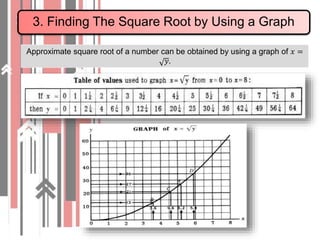
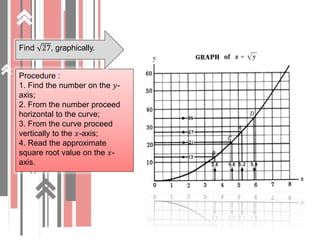
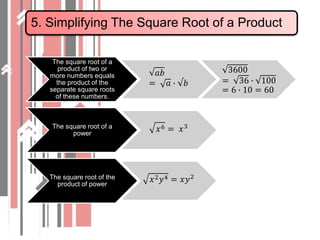
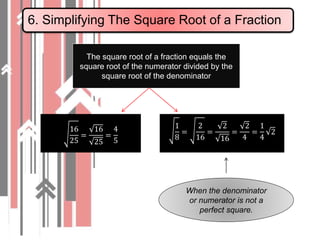
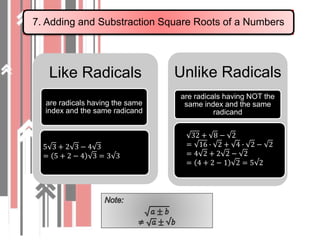
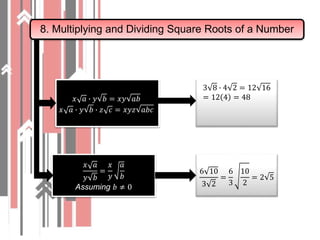
This document discusses various topics related to roots and radicals: 1. It defines roots and radicals, and explains the difference between rational and irrational numbers. Square roots can be estimated using graphs or tables. 2. The square root of a product equals the product of the square roots. Square roots of fractions are simplified by taking the square root of the numerator and denominator. 3. Adding, subtracting, multiplying and dividing square roots follows specific rules. Rationalizing the denominator of a fraction involves multiplying by the conjugate to eliminate radicals. 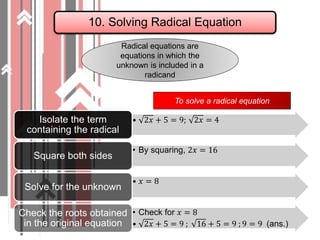4. Radical equations are solved by isolating the radical term, squaring both sides, then solving for the unknown variable and checking the solution in the original equation.

1. ROOTS
AND
RADICALS
CHAPTER 12

2. BY GROUP 12 :
MEUTIAH NAHRISYAH
• 1711441014
NIATI INDAN
• 1711441013

3. SECTION 1. Understanding Roots and Radicals
2. Understanding Rational and Irrational Number
3. Finding The Square Root of a Number by Using a Graph
4. Finding The Square Root of a Number by Using a Table
5. Simplifying The Square Root of a Product
6. Simplifying The Square Root of a Fraction
7. Adding and Subtraction Square Roots of a Numbers
8. Multiplying and Dividing Square Roots of a Numbers
9. Rationalizing The Dominator of Fraction
10. Solving Radical Equation

4. Opposite of squaring number is taking the square root of a number.
The square root of a number is one of its two equal factors.
Principal
Square
Roots
Positive
√𝑥
Negative
−√𝑥

5. 𝑛
𝑥
radical
radicand
index
Parts of a Radical
Expression
 Note : If no index is
written, it is assumed to
be 2
Nth Roots
Other roots can be found, as weel
The nth root of 𝑎 is defined as
𝑛
𝑎 = 𝑏 only if 𝑏 𝑛
= 𝑎
If the index n is even, the root is NOT a real number when 𝑎 is negative.
If the index is odd, the root will be a real number when 𝑎 is negative.

6. 2. Understanding Rational and Irrational Number
Rational
All Integers
Fractions
1.5
2
=
3
4
Decimals 0.666… =
2
3
Square root
expression
25,
3
27, 𝑒𝑡𝑐

7. Irrational
2 = 1.4142 ; 3
= 1.732 ; 𝑒𝑡𝑐
𝜋
√5
2
,
2
√5
, 2 + 7, 𝑒𝑡𝑐

8. 3. Finding The Square Root by Using a Graph
Approximate square root of a number can be obtained by using a graph of 𝑥 =
𝑦.

9. Procedure :
1. Find the number on the 𝑦-
axis;
2. From the number proceed
horizontal to the curve;
3. From the curve proceed
vertically to the 𝑥-axis;
4. Read the approximate
square root value on the 𝑥-
axis.
Find 27, graphically.

10. 4. Finding The Square Root by Using a Table
[Using the table on page 290] To find the principal square root of a number, look
for the number the number under 𝑁. Read the square root of the number under
𝑁, immediately to the right of the number.
Example:
5 = 2.236

11. 5. Simplifying The Square Root of a Product
The square root of a
product of two or
more numbers equals
the product of the
separate square roots
of these numbers.
𝑎𝑏
= 𝑎 ∙ √𝑏
3600
= 36 ∙ 100
= 6 ∙ 10 = 60
The square root of a
power
𝑥6 = 𝑥3
The square root of the
product of power
𝑥2 𝑦4 = 𝑥𝑦2

12. 6. Simplifying The Square Root of a Fraction
The square root of a fraction equals the
square root of the numerator divided by the
square root of the denominator
16
25
=
16
25
=
4
5
1
8
=
2
16
=
2
16
=
2
4
=
1
4
2
When the denominator
or numerator is not a
perfect square.

13. 7. Adding and Substraction Square Roots of a Numbers
Like Radicals
are radicals having the same
index and the same radicand
5 3 + 2 3 − 4 3
= 5 + 2 − 4 3 = 3√3
Unlike Radicals
are radicals having NOT the
same index and the same
radicand
32 + 8 − 2
= 16 ∙ 2 + 4 ∙ 2 − 2
= 4 2 + 2 2 − 2
= 4 + 2 − 1 2 = 5√2

14. 8. Multiplying and Dividing Square Roots of a Number
𝑥 𝑎 ∙ 𝑦 𝑏 = 𝑥𝑦 𝑎𝑏
𝑥 𝑎 ∙ 𝑦 𝑏 ∙ 𝑧 𝑐 = 𝑥𝑦𝑧 𝑎𝑏𝑐
3 8 ∙ 4 2 = 12 16
= 12 4 = 48
𝑥 𝑎
𝑦 𝑏
=
𝑥
𝑦
𝑎
𝑏
Assuming 𝑏 ≠ 0
6 10
3 2
=
6
3
10
2
= 2 5

15. 9. Rationalizing The Denominator of a Fraction
This process involves multiplying the quotient by a form of
that will eliminate the radical in the denominator
4
2
=
4
2
∙
2
2
=
4 2
2
= 2 2
3 + 2
2 + √3
∙
2 − 3
2 − 3
=
6 − 3 + 2 2 − 2 3
2 − 3
=
6 − 3 + 2 2 − 2 3
−1
= − 6 − 3 + 2 2 − 2√3
To rationalize the denominator of a fraction is to change the
denominator from an irrational number to a rational number.
Note: we need to multiply by the conjugate of the
denominator. The conjugate uses the same terms, but the
opposite operation.

16. 10. Solving Radical Equation
Radical equations are
equations in which the
unknown is included in a
radicand
• 2𝑥 + 5 = 9; 2𝑥 = 4Isolate the term
containing the radical
• By squaring, 2𝑥 = 16
Square both sides
• 𝑥 = 8
Solve for the unknown
• Check for 𝑥 = 8
• 2𝑥 + 5 = 9 ; 16 + 5 = 9 ; 9 = 9 (ans.)
Check the roots obtained
in the original equation
To solve a radical equation

17. ANY QUESTION