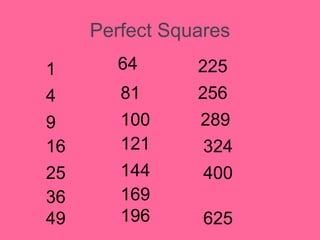
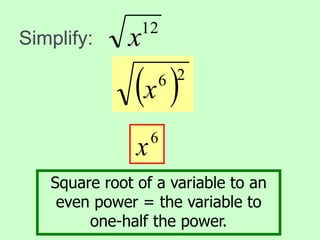
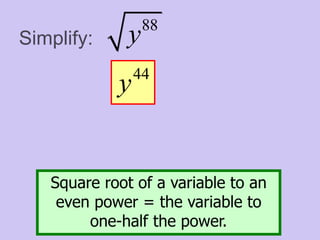
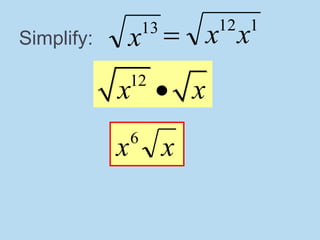
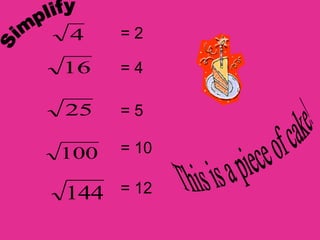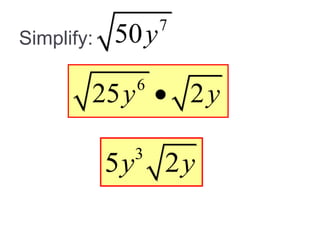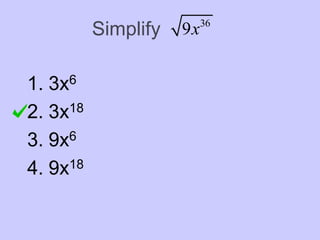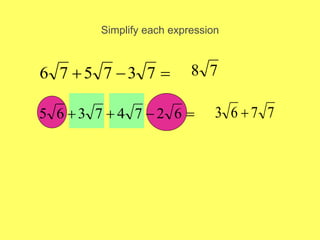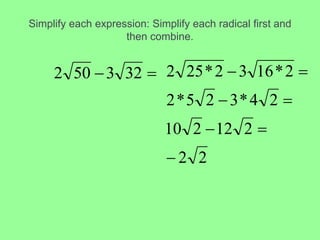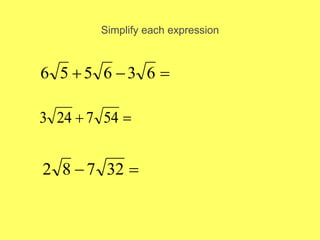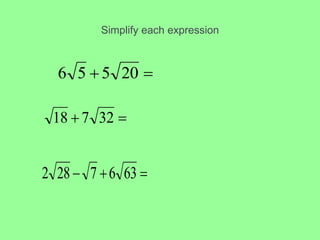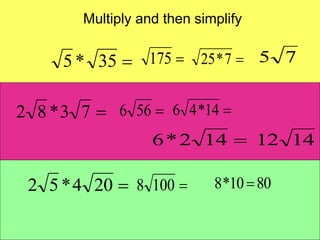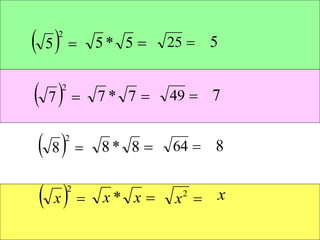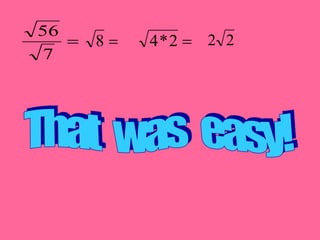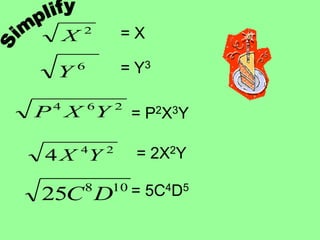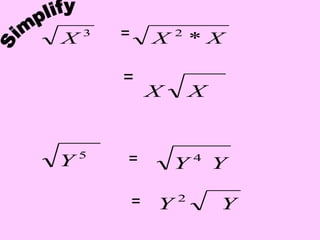This document provides an introduction to radicals and radical expressions. It defines key radical terms such as radicand, index, principal and negative square roots, and perfect squares. It also covers how to simplify, add, subtract, multiply and divide radical expressions through applying properties of radicals and rationalizing denominators. The goal is to leave radicals in the simplest form with no perfect square factors in the radicand.

1. Introduction to Radicals

2. If b 2 = a, then b is a square root of a.
Meaning Positive
Square Root
Negative
Square Root
The positive and
negative square
roots
Symbol
Example
 
3
9  3
9 

 3
9 



3. Radical Expressions
Finding a root of a number is the inverse operation of raising
a number to a power.
This symbol is the radical or the radical sign
n
a
index
radical sign
radicand
 The expression under the radical sign is the
radicand.
 The index defines the root to be taken.

4. • square root: one of two equal factors of a given number. The radicand is like the
“area” of a square and the simplified answer is the length of the side of the squares.
• Principal square root: the positive square root of a number; the principal square
root of 9 is 3.
• negative square root: the negative square root of 9 is –3 and is shown like
• radical: the symbol which is read “the square root of a” is called a radical.
• radicand: the number or expression inside a radical symbol --- 3 is the
radicand.
• perfect square: a number that is the square of an integer. 1, 4, 9, 16, 25, 36, etc…
are perfect squares.
3
9 
3
9 


3

5. Square Roots
If a is a positive number, then
a is the positive (principal) square
root of a and
100 
a
 is the negative square root of a.
A square root of any positive number has two roots –
one is positive and the other is negative.
Examples:
10
25
49

5
7
1
1 
36
  6

9
  non-real #

 81
.
0 9
.
0


6. What does the following symbol represent?
The symbol represents the positive or
principal root of a number.
4 5xy
What is the radicand of the expression ?
5xy

7. What does the following symbol represent?
The symbol represents the negative root of
a number.

3 5
2
5 y
x
What is the index of the expression ?
3

8. What numbers are perfect
squares?
1 • 1 = 1
2 • 2 = 4
3 • 3 = 9
4 • 4 = 16
5 • 5 = 25
6 • 6 = 36
49, 64, 81, 100, 121, 144, ...

9. Perfect Squares
1
4
9
16
25
36
49
64
81
100
121
144
169
196
225
256
324
400
625
289

10. 4
16
25
100
144
= 2
= 4
= 5
= 10
= 12

11. Simplifying Radicals

12. Simplifying Radical
Expressions
100 4 25
 
36 4 9
 
3
2
6 

Product Property for Radicals
ab a b
 
10 2 5
 
36 4 9
 

13. Simplifying Radical Expressions
• A radical has been simplified when its radicand
contains no perfect square factors.
• Test to see if it can be divided by 4, then 9, then
25, then 49, etc.
• Sometimes factoring the radicand using the
“tree” is helpful.
Product Property for Radicals
50 25 2
  5 2

14 7
x x


14. 8
20
32
75
40
=
=
=
=
=
2
*
4
5
*
4
2
*
16
3
*
25
10
*
4
=
=
=
=
=
2
2
5
2
2
4
3
5
10
2
Perfect Square Factor * Other Factor
LEAVE
IN
RADICAL
FORM

15. 48
80
50
125
450
=
=
=
=
=
3
*
16
5
*
16
2
*
25
5
*
25
2
*
225
=
=
=
=
=
3
4
5
4
2
5
5
5
2
15
Perfect Square Factor * Other Factor
LEAVE
IN
RADICAL
FORM

16. Steps to Simplify Radicals:
1. Try to divide the radicand into a perfect
square for numbers
2. If there is an exponent make it even by
using rules of exponents
3. Separate the factors to its own square
root
4. Simplify

17. Simplify:
12
x
6
x
 2
6
x
Square root of a variable to an
even power = the variable to
one-half the power.

18. Simplify:
88
y
44
y
Square root of a variable to an
even power = the variable to
one-half the power.

19. Simplify:
13
x
x
x6
12
x x

1
12
x
x


20. Simplify:
7
50y
3
5 2
y y
6
25 2
y y


21. Simplify
1. .
2. .
3. .
4. .
2 18
72
3 8
6 2
36 2

22. Simplify 36
9x
1. 3x6
2. 3x18
3. 9x6
4. 9x18

23. +
To combine radicals: combine
the coefficients of like radicals

24. Simplify each expression


 7
3
7
5
7
6 7
8



 6
2
7
4
7
3
6
5 7
7
6
3 

25. Simplify each expression: Simplify each radical first and
then combine.

 32
3
50
2
2
2
2
12
2
10
2
4
*
3
2
5
*
2
2
*
16
3
2
*
25
2








26. Simplify each expression: Simplify each radical first and
then combine.

 48
5
27
3
3
29
3
20
3
9
3
4
*
5
3
3
*
3
3
*
16
5
3
*
9
3







27. 18
288
75
24
72
=
=
=
=
=
=
=
=
=
=
Perfect Square Factor * Other Factor
LEAVE
IN
RADICAL
FORM

28. Simplify each expression


 6
3
6
5
5
6

 54
7
24
3

 32
7
8
2

29. Simplify each expression

 20
5
5
6

 32
7
18


 63
6
7
28
2

30. *
To multiply radicals: multiply the
coefficients and then multiply
the radicands and then simplify
the remaining radicals.

31. 
35
*
5 
175 
7
*
25 7
5
Multiply and then simplify

7
3
*
8
2 
56
6 
14
*
4
6

14
2
*
6 14
12

20
4
*
5
2 
100
8 80
10
*
8 

32.   
2
5 
5
*
5 
25 5
  
2
7 
7
*
7 
49 7
  
2
8 
8
*
8 
64 8
  
2
x 
x
x * 
2
x x

33. To divide radicals:
divide the
coefficients, divide
the radicands if
possible, and
rationalize the
denominator so that
no radical remains in
the denominator

34. 
7
56

8 
2
*
4 2
2

35. 
7
6
This cannot be
divided which leaves
the radical in the
denominator. We do
not leave radicals in
the denominator. So
we need to
rationalize by
multiplying the
fraction by something
so we can eliminate
the radical in the
denominator.

7
7
*
7
6

49
42
7
42
42 cannot be
simplified, so we are
finished.

36. This can be divided
which leaves the
radical in the
denominator. We do
not leave radicals in
the denominator. So
we need to
rationalize by
multiplying the
fraction by something
so we can eliminate
the radical in the
denominator.

10
5

2
2
*
2
1
2
2

37. This cannot be
divided which leaves
the radical in the
denominator. We do
not leave radicals in
the denominator. So
we need to
rationalize by
multiplying the
fraction by something
so we can eliminate
the radical in the
denominator.

12
3

3
3
*
12
3

36
3
3

6
3
3
2
3
Reduce
the
fraction.

38. 2
X
6
Y
2
6
4
Y
X
P
2
4
4 Y
X
10
8
25 D
C
= X
= Y3
= P2X3Y
= 2X2Y
= 5C4D5

39. 3
X
X
X
=
=
X
X *
2
Y
Y 4
5
Y
=
= Y
Y 2